§ 6. Сокристаллизация со специфическими носителями при отсутствии изоморфизма 1 рода

     Рассмотренные выше закономерности сокристаллизации относились к процессам соосаждения, приводящим к образованию истинных смешанных кристаллов (изовалентный изоморфизм, изоморфизм I рода).

     Однако существует большое число систем, для которых и при отсутствии изоморфизма 1 рода имеет место со кристаллизация радиоактивных элементов (радиоактивных нуклидов) с соответствующим носителями. Если закономерности процессов сокристаллизации с образованием истинных смешанных кристаллов изучены достаточно полно, то этого нельзя сказать о других случаях сокристаллизации ввиду многообразия и малой изученности механизмов протекания этих процессов. Тем не менее эти случаи сокристаллизации также имеют большое практическое значение для целей выделения и концентрирования радиоактивных элементов (радиоактивных нуклидов).

     Все случаи сокристаллизации при отсутствии изовалентного изоморфизма можно формально разделить на два основных типа: с образованием кристаллов Гримма и аномальных смешанных кристаллов.

     Кристаллы Гримма отвечают условиям изоморфизма II и III рода. Примерами таких систем являются BaSO₄—КМnO₄, RbC1O₄ — RaSO₄, BaSO₄ — KBF₄, NaBr — PbS и др. Для объяснения механизма образования кристаллов Гримма В. Г. Хлопин с сотрудниками выдвинули следующую гипотезу. Поверхность растущего кристалла обладает сильным электрическим полем; способным притягивать и удерживать как собственные, так и посторонние ионы. Собственные ионы входят в кристаллическую решетку и могут удерживать противоположно заряженные ионы. Посторонние остаются во внешней обкладке двойного слоя и постепенно вытесняются обратно в раствор. Так, при кристаллизации КМnO₄ из раствора, содержащего RaSO₄, на поверхности кристалла адсорбируются ионы Ra²⁺ и SO^2-₄. При этом энергетически выгоднее, чтобы они адсорбировались группами при дополнительном связывании взаимным притяжением. Адсорбируясь вместе, эти ионы могут образовать участок решетки RaSO₄. Поскольку размеры решеток RaSO₄ и КМnO₄ близки, то оба компонента могут принимать участие в построении общей кристаллической решетки. При этом наиболее вероятно, что замещение происходит двумерными, а не трехмерными элементами решетки. Совершенно естественно, что образование кристаллов Гримма может иметь, место лишь при одновременной встрече на поверхности кристалла КМnO₄ ионов Ra²⁺ и SO^2-₄ в количестве, необходимом для построения элементарной ячейки RaSO₄, участвующей в замещении. Отсюда становится понятным характерное для кристаллов Гримма наличие нижней границы смешиваемости. Естественно, что концентрация радиоактивного элемента, отвечающая нижней границе смешиваемости, зависит от степени сложности кристаллической ячейки, участвующей в замещении, и лежит в пределах 10^-3 — 10^-9 моль/л. Увеличение концентрации сопряженного иона (например, SO^2-₄ - в системе КМnO₄—RaSO₄—H₂O) понижает нижнюю границу смешиваемости; добавление посторонних ионов повышает ее.

     Кристаллы Гримма можно рассматривать как коллоидные системы. Подобно тому как по степени дисперсности растворенного вещества различают истинные и коллоидные растворы, так по степени дисперсности компонентов, замещающих друг друга в кристаллической решетке, разделяют истинные смешанные кристаллы и кристаллы Гримма.

     Аномальные смешанные кристаллы — это кристаллы, в которых замещение происходит с изменением числа частиц в кристаллической структуре (т. е. для данных систем не соблюдаются условия изоморфизма I, II и III рода). Примерами систем, в которых имеет место образование таких кристаллов, могут служить:

     NH₄Cl - хлориды тяжелых металлов (Fe³⁺, Cr³⁺, Mn²⁺, Cu²⁺, Co²⁺ и др.) - H₂O      K₂SO₄ - Me³⁺₂(SO₄)₃ - H₂O      (Me³⁺ - Ce³⁺, La³⁺, Am³⁺ и др.)      U(C₂O₄)₂ - Ce₂(C₂O₄)₃ - H₂O      LaF₃ - Me²⁺F₂ - H₂O      (Me²⁺ - Ca²⁺, Sr²⁺, Ra²⁺)      Ba(NO₃)₂ - метиленовая синь - H₂O и т.д.

Единой точки зрения на механизм образования аномальных смешанных кристаллов не существует. Различие свойств и характера компонентов, составляющих аномальные смешанные кристаллы, обусловливает многообразие механизмов их образования. Такими механизмами являются следующие:    1) компенсация зарядов за счет образования вакансий (изоморфизм вычитания), например LiCl — MgCl₂ (2Li+ замещаются на Mg²⁺);    2) компенсация зарядов за счет заполнения пространства (изоморфизм с внедрением), например CaF₂ — YF₃ (Y³⁺ замещает Ca²⁺ при одновременном внедрении F^- в междоузлия);    3) замещение нескольких ионов разного знака комплексным ионом при сохранении суммы зарядов и близкой структурной аналогии (например, замещение 2NH⁺₄ и 4С1^- на ион [MnCl₄(H₂O)₂]^2- в системе NH₄Cl—MnCl₂—H₂O);    4) замещение участков кристаллической решетки аналогичными по структуре (трехмерная или двумерная аналогия) участками соединений второго компонента (например, система Ва(NО₃)₂ — метиленовая синь—H₂O). Этот механизм аналогичен механизму образования кристаллов Гримма.

     Для рассмотрения количественных закономерностей процессов сокристаллизации с образованием аномальных смешанных кристаллов следует разграничить два вида систем: 1) системы, твердую фазу в которых можно рассматривать с точки зрения термодинамики как истинный твердый раствор и 2) системы, твердая фаза которых рассматривается как коллоидный твердый раствор.

     Рассмотрим количественные соотношения, которые могут быть выведены из теории Ратнера при допущении, что образующиеся смешанные кристаллы можно считать с термодинамической точки зрения одной твердой фазой. Это допущение предполагает приложимость к таким системам закона Хлопина и отсутствие для них нижней границы смешиваемости. Действительно, для целого ряда аномальных смешанных кристаллов экспериментально не установлено нижней границы смешиваемости (например, NН₄Сl — Me²⁺Cl₂ — H₂O, где Me²⁺ — Cu²⁺, Mn²⁺; K₂SO₄ — Me³⁺₂(SO₄)₃ — Н₂O, где Me³⁺ — Ce³⁺, La³⁺, Am³⁺, и др).

     Рассмотрим систему Cn₃Bn₄ —An₁Bn₂ — H₂O, где An₁Bn₂ —соосаждающийся компонент; Сn₃Вn₃ — носитель. Для этой системы уравнение (5.21) имеет вид

(5.30)

     Умножим обе части этого равенства на значение термодинамической активности вещества-носителя в его насыщенном растворе:

     a_n = a_n±⁽ⁿ₃ ^{+ n}₄⁾ = (m_n±_n±)⁽ⁿ₃ ^{+ n}₄⁾ = mⁿ_3n+ ⁿ_3n+ mⁿ_4n- ⁿ_4n-.

Тогда

.

(5.31)

Отсюда

,

(5.32)

где ПА — произведение активности соответствующих соединений в их насыщенных растворах; m_n-⁽ⁿ₂ ^-n ₄⁾ = m_i-ⁿ₂ / m_n-ⁿ₄, так как m_i- = m_n- и отвечает концентрации общего аниона.

     Как следует из уравнения (5.32), значение D₀ для случая образования аномальных смешанных кристаллов этого вида в отличие от истинных зависит от концентрации общего иона (аниона или катиона), а значит, и от концентрации макрокомпонента в жидкой фазе.

     Уравнение (5.32) объясняет наблюдаемую экспериментально зависимость коэффициента кристаллизации от концентрации макрокомлонента и переходит в уравнение Ратнера для истинных смешанных кристаллов (при n₂ = n₄).

     С точки зрения энергетической теории аномальные смешанные кристаллы, как и кристаллы Гримма, должны обладать ограниченной смешиваемостью. Тем не менее имеющиеся экспериментальные данные весьма противоречивы.

     Следует отметить, что вопрос об отсутствии нижней границы смешиваемости для аномальных смешанных кристаллов нельзя считать окончательно решенным. Это связано прежде всего с тем, что почти все исследования по соосаждению с образованием аномальных смешанных кристаллов проводились в относительно узком интервале концентраций радиоактивных элементов с нижним пределом 10^-8 — 10^-9 моль/л. Расширение диапазона в область более низких концентраций может привести к изменению коэффициента кристаллизации. Это особенно существенно для систем, в которых переход радиоактивного элемента в твердую фазу связан с образованием комплексных анионов. Так, исследование зависимости коэффициента кристаллизации от концентрации свинца в жидкой фазе для двух похожих систем (NH₄C1 — PbCl₂ — H₂O и NH₄I—РbI₂—H₂O) привело к совершенно различным результатам. Для первой из этих систем установлено наличие нижней границы смешиваемости, а для второй нет. Это можно объяснить большей устойчивостью ионов РbI_-3 по сравнению с PbCl_-3, в виде которых происходит внедрение свинца в кристаллическую решетку солей аммония.

     Значительно менее изучены количественные закономерности процессов сокристаллизации с образованием аномальных смешанных кристаллов, рассматриваемых как коллоидные твердые растворы. К таким системам относятся: NH₄C1—Ме³⁺Сl₃—H₂O (где Me³⁺—Fe³⁺, Cr³⁺), LaF₃—MeFn—H₂O (где Me — Ra²⁺, Th⁴⁺), неорганическая соль — органический краситель — вода и т. д. В таких кристаллах второй компонент находится не в виде отдельных молекул, или ионов, а в виде крупных агрегатов большей частью неопределенного состава. Это обусловливает наличие для подобных систем нижней границы смешиваемости. Закон Хлопина применим к ним, как и в случае кристаллов Гримма, лишь формально. Для этих систем, так же как и для кристаллов Гримма, имеет место статистически равномерное распределение радиоактивного элемента в кристаллах вещества-носителя. Однако наличие нижней границы смешиваемости и зависимость коэффициента кристаллизации от концентрации радиоактивного элемента указывают на неприложимость к этим системам закона Хлопина.
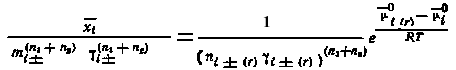
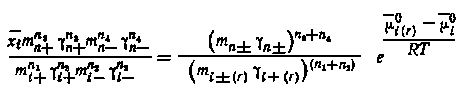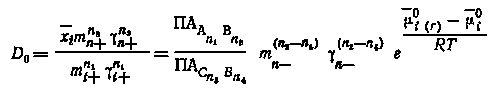