§ 4 Факторы, влияющие на процесс соосаждения со специфическими носителями

     Как следует из предыдущего изложения,

      значения константы распределения К_N и коэффициента кристаллизации D характеризуют степень перехода радиоактивного элемента в кристаллическую. фазу специфического носителя.

     Представляет интерес выяснить, какие факторы влияют на значения констант К_N, и D и в какой мере можно управлять процессами соосаждения радиоактивных элементов со специфическими носителями. Ответ на эти вопросы дает теория А. П. Ратнера, которая исходит из того, что термодинамическое равновесие между кристаллической фазой и раствором может быть рассмотрено применительно как к веществу радиоактивного элемента, так и к веществу носителя.

     Рассмотрим вначале два случая равновесия между кристаллической фазой и раствором в отношении радиоактивного элемента. 1) равновесие между смешанными кристаллами, содержащими радиоактивный элемент и носитель, и раствором, насыщенным в отношении вещества носителя и содержащим микроколичества радиоактивного элемента; 2) равновесие между кристаллической фазой соединения радиоактивного элемента и его насыщенным раствором.

     В   п е р в о м   с л у ч а е,   как указывалось ранее, условием термодинамического равновесия является равенство химических потенциалов радиоактивного элемента в равновесных фазах:

i = i,

(5.12)

Причем

i = 0i + RT lnai = 0i + RT ln (xii)

(5.13)

и

i = 0i + RT ln ai = 0i + RT ln (mii)

(5.14)

где а_i и а_i — термодинамические активности вещества радиоактивного элемента в твердой и жидкой фазах; х_i — молярная доля вещества радиоактивного элемента в твердой фазе; m_i — молярная концентрация вещества радиоактивного элемента в жидкой фазе; _i и _i — коэффициенты активности вещества радиоактивного элемента в твердой и жидкой фазах; _i⁰ и _i⁰ — стандартные химические потенциалы вещества радиоактивного элемента в соответствующих фазах.

     Термодинамическая активность вещества радиоактивного элемента в жидкой фазе может быть выражена через среднеионные активности а_i±:

ai = ai± = a+i+ a-i- = mi±i±,

(5.15)

где + и - — числа катионов и анионов, образующихся при диссоциации соединений радиоактивного элемента и носителя;  = + + - — общее число ионов , на которые диссоциируют молекулы веществ радиоактивного элемента и носителя; - средняя молярная концентрация вещества радиоактивного элемента в жидкой фазе; - среднеионный коэффициент активности вещества радиоактивного элемента в жидкой фазе.

     Стандартное состояние i-го компонента в твердой фазе соответствует крайне разбавленному твердому раствору, когда x_i  0 и _i  1.

     В жидкой фазе стандартное состояние отвечает бесконечно разбавленному раствору, ионная сила которого I  0 и _i  1.

     Так как нас интересует твердый раствор, крайне разбавленный в отношении радиоактивного элемента (_i = 1), то из выражений (5.12) — (5.15) получаем

(5.16)

     Для    в т о р о г о    с л у ч а я    условие термодинамического равновесия между кристаллической фазой вещества радиоактивного элемента и его насыщенным раствором может быть представлено следующим образом:

i(r) = i(r),

(5.17)

причем

i(r) = 0i(r) + RT ln xi(r) i(r) = 0i(r).

(5.18)

Тогда:

i(r) = 0i + RT ln ai(r) = 0i + RT ln mi(r)i(r).

(5.19)

где x_i(r) = 1 — молярная доля вещества радиоактивного элемента в твердой фазе, образованной чистым веществом радиоактивного элемента; a_i(r) и m_i(r) — термодинамическая активность и молярная концентрация вещества радиоактивного элемента в его насыщенном растворе; ⁰_i(r), и ⁰_i(r) — стандартные химические потенциалы вещества радиоактивного элемента в соответствующих фазах.

     Стандартное состояние в жидкой фазе для второго случая равновесия остается тем же, что и для первого случая. Для твердой фазы, представляющей собой кристаллы соединения радиоактивного элемента, имеем

     _i(r) = ⁰_i(r),

так, как _i(r) = 1 при x_i(r) = 1.

     Тогда из выражений (5.17) - (5.19) и (5.15) получаем

i(r) = 0i(r) = 0i + RT ln (mi±(r) i±(r))

(5.20)

Подставляя ⁰_i из равенства (5.20) в выражение (5.16), имеем

(5.21)

     Умножим обе части равенства (5.21) на a_n / x_n, где a_n = (а_n±)^ = (m_n±_n±)^ — термодинамическая активность вещества носителя в его насыщенном растворе, x_n — молярная доля вещества носителя в твердой фазе. Тогда имеем

(5.22)

     Учитывая, что x_n = 1 и m^-_n- = m^-_i- (для систем с общим анионом*), левая часть уравнения (5.22) может быть представлена следующим образом:

(5.23)

     Величина D₀ была названа А. П. Ратнером истинной константой фракционирования, так как она в отличие от экспериментально определяемого коэффициента кристаллизации D не зависит от состава жидкой фазы.

     С другой стороны, как видно из уравнения (5.23), значение коэффициента кристаллизации зависит от свойств чистых компонентов (носителя и радиоактивного элемента), а также свойств бесконечно разбавленного твердого раствора. Действительно, так как

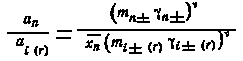      то

(5.24)

     Коэффициент кристаллизации D с учетом выражений (5.23) и (5.24) может быть представлен следующим образом:

(5.25)

     Рассмотрим влияние различных факторов на процесс соосаждения радиоактивных элементов со специфическими носителями с позиций теории Ратнера. Уравнение (5.25) является собственно уравнением Ратнера. Из этого уравнения видно, что значение коэффициента кристаллизации определяется тремя факторами:    1) отношением термодинамических активностей соединений носителя и радиоактивного элемента в их насыщенных растворах. Этот фактор зависит от характера системы и вещества носителя. Критерием оптимального выбора носителя является максимальное значение отношения термодинамических активностей веществ в их насыщенных растворах**;

     e^(0_i(r) ^{- 0}_i^)/RT,

   2) экспоненциальным множителем учитывающим отклонение свойств образующихся смешанных кристаллов oт идеальных. При этом разность ⁰_i(r) — ⁰_i представляет собой работу, необходимую для переноса 1 моль радиоактивного элемента из его чистых кристаллов в бесконечно разбавленный твердый раствор. Этот фактор также зависит от характера системы, особенно от степени близости кристаллохимических характеристик соединений носителя и радиоактивного элемента, а также от концентрации радиоактивного элемента в твердой фазе и от температуры;    3) отношением среднеионных коэффициентов активности соединений радиоактивного элемента и элемента носителя в их общем растворе (_i± / _n±)^. Этот фактор определяется как природой сокристаллизующихся соединений, так и составом жидкой фазы, от которого зависит значение ионной силы раствора.

     Таким образом, теория Ратнера позволяет обосновать оптимальный выбор специфического носителя для определенного радиоактивного элемента или нуклида. Однако практически из-за отсутствия значений коэффициентов активности и химических потенциалов компонентов в твердых растворах в настоящее время на основании теории выбор носителя неосуществим и в подавляющем большинстве случаев носитель подбирается экспериментально.

     Для выбранной системы носитель — радиоактивный элемент (радиоактивный нуклид) эффективностью соосаждения можно управлять, используя зависимость коэффициентов активности от состава жидкой фазы и температуры.

     Состав жидкой фазы влияет на значение коэффициента кристаллизации через отношение термодинамических активностей ионов радиоактивного элемента и носителя а_i/а_n. Это отношение можно регулировать за счет неодинакового изменения коэффициентов активности при добавлении посторонних электролитов, а также за счет избирательного связывания одного из компонентов системы в соединения, не участвующие в изоморфном замещении (малодиссоциированные, комплексные). Преимущественное связывание радиоактивного элемента приводит к уменьшению коэффициента кристаллизации, в то время как связывание элемента-носителя — к его возрастанию.

     Влияние температуры на коэффициент кристаллизации индивидуально и определяется характером системы.

     Процесс изоморфной сокристаллизации можно рассматривать как распределение радиоактивного элемента между двумя несмешивающимися растворителями или как ионообменную гетерогенную реакцию. Рассмотрим гетерогенную реакцию

     ВаСl₂ + RaCl₂  ВаСl₂ + RaCl₂;

     Константа равновесия этой реакции может быть представлена выражением K_р = a_ia_n/(a_ia_n), где индексы n и i относятся соответственно к барию и радию. Учитывая, что

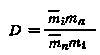      , имеем .

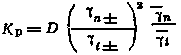Так как для носителя в твердой фазе x_n  1 и _n  1, получаем

      .

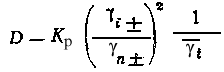Значение константы равновесия изменяется с темпера турой в соответствии с уравнением

      , где H⁰ — изменение стандартной энтальпии.

     Кроме того, температура влияет на отношение _i±/_n±, что обусловлено неодинаковым изменением парциальных моляльных энтальпий компонентов в их общем растворе.

     И, наконец, с температурой изменяется коэффициент активности радиоактивного элемента в твердой фазе, так как

     _i = e^-0_i^/RT = e^-(H0_i ^{- TS0}_i^)/RT и , где H⁰_i - изменение парциальной стандартной энтальпии.

     Сложный характер зависимости коэффициента кристаллизации от температуры объясняется одновременным влиянием ее на все рассмотренные выше факторы. Как показывают экспериментальные исследования, при микроконцентрациях радиоактивного элемента влияние температуры на коэффициент кристаллизации в основном обусловлено изменением экспоненциального множителя в уравнении Ратнера. Для различных систем может наблюдаться увеличение, уменьшение или неизменность значений D с изменением температуры.

• Для систем с общим катионом m^+_n+ = m^+_n+.    ** Ранее при выборе носителя руководствовались отношением растворимостей соединений радиоактивного элемента и носителя (что некорректно).