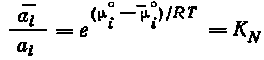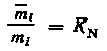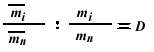- •В.Д.Нефедов е.Н.Текстер м.А.Торопова радиохимия
- •Глава 1
- •§ 1. Предмет радиохимии
- •§ 2. Краткий очерк истории развития радиохимии
- •§ 3. Особенности радиохимии
- •§ 4. Значение радиохимии
- •1 Общая радиохимия глава 2
- •§ 1. Общехимические свойства изотопных частиц
- •2. Термодинамическое поведение изотопных частиц
- •3. Кинетическое поведение изотопных частиц
- •Глава 3
- •§ 1. Классификация реакций изотопного обмена
- •§ 2. Причины протекания реакций изотопного обмена
- •3. Особенности реакций идеального изотопного обмена
- •§ 4. Основное уравнение кинетики реакций идеального изотопного обмена
- •§ 5. Основы экспериментальных методов исследования процессов изотопного обмена
- •Глава 4
- •§ 1. Состояние радиоактивных элементов [нуклидов] в жидкой фазе
- •§ 2. Процессы радиоколлоидообразования
- •§ 3. Основы экспериментальных методов исследования радиоколлоидов
- •Глава 5
- •§ 1. Закономерности процессов соосаждения с изотопными носителями
- •§ 2. Основные области применения изотопных носителей
- •§ 3. Принцип действия и закономерности процессов соосаждения со специфическими носителями
- •§ 4 Факторы, влияющие на процесс соосаждения со специфическими носителями
- •§ 5. Особенности процессов соосаждения со специфическими носителями
- •§ 6. Сокристаллизация со специфическими носителями при отсутствии изоморфизма 1 рода
- •§ 7. Основы экспериментальных методов исследования процессов соосаждения со специфическими носителями
- •§ 8. Основные области применения специфических носителей
- •Глава 6
- •§ 1. Первичная адсорбция
- •§ 2. Вторичная обменная адсорбция
- •§ 3. Закономерности процесса соосаждения с неспецифическими носителями
- •§ 4. Соосаждение с неспецифическими носителями при образовании внутренне-адсорбционных систем
- •§ 5. Основы экспериментальных методов исследования процессов соосаждения с неспецифическими носителями
- •§ 6. Основные области применения неспецифических носителей
- •§ 7. Методы разграничения различных видов соосаждения
- •Глава 7
- •§ 1. Закономерности и классификация экстракционных процессов
- •§ 3. Практическое использование процессов экстракции
- •Глава 8
- •§ 1. Основные закономерности хроматографических процессов Ионообменная хроматография.
- •Распределительная хроматография.
- •См.: Егоров е. В., Макарова с. Б. Ионный обмен в радиохимии. М., Атомиздат, 1971. § 2. Основы экспериментальных методов хроматографического исследования
- •См.: Роберте т. Радиохроматография. М., Мир, 1981. § 3. Примеры практического использования хроматографических методов в радиохимии
- •Глава 9
- •§ 1. Закономерности электрохимических процессов
- •§ 2 Особенности поведения радиоактивных элементов (нуклидов) при электрохимических процессах
- •§ 3. Основы экспериментальных методов исследования электрохимических процессов
- •§ 4. Использование электрохимических процессов в радиохимии
- •2 Химия радиоактивных элементов
- •Глава 10
- •§ 1. Технеций
- •§ 2. Прометий
- •§ 3. Полоний
- •§ 4. Астат
- •§ 5. Радон
- •§ 6. Франций
- •§ 7. Радий
- •Глава 11
- •§ 1. История открытия актиния и актиноидов
- •§ 2. Важнейшие изотопы актиния и актиноидов, методы их получения и идентификации
- •§ 3. Физические свойства актиния и актиноидов
- •§ 4. Актиний
- •§ 5. Торий
- •§ 6. Протактиний
- •§ 7. Уран, нептуний, плутоний и америций
- •§ 8. Трайсамерициевые актиноиды
- •Глава 12
- •§ 1. История открытия
- •§ 2 Методы получения и идентификации
- •3 Химические последствия радиоактивного распада
- •Глава 13
- •§ 1. История открытия ядерной изомерии
- •§ 2. Особенности явления ядерной изомерии
- •§ 3. Химические последствия изомерных переходов
- •§ 4. Практическое использование химических последствий изомерного перехода
- •Глава 14
- •§ 1. Теоретические аспекты химических последствий --распада
- •§ 2. Экспериментальные методы исследования химических последствий --распада
- •§ 3. Практическое использование химических последствий --распада
§ 3. Принцип действия и закономерности процессов соосаждения со специфическими носителями
Принципиальной основой действия специфических носителей являются процессы иоморфной сокристаллизации.
Явление изоморфизма было открыто Э. Митчерлихом в 1819 г. на примере КН2PO4, KH2AsO4 и NH4H2PO4. По Митчерлиху, изоморфными являются вещества, сходные в химическом отношении, обладающие одинаковой кристаллической формой и способные образовывать смешанные кристаллы.
Исследования Митчерлиха сыграли большую роль в развитии систематики химических элементов. Д. И. Менделеев указывал, что изоморфизм являлся исторически первым и доказательным методом установления сходства двух разных элементов. Исключительно важное значение для дальнейшего развития теории изоморфизма имел метод рентгеноструктурного анализа и использование его для определения кристаллической структуры веществ. Опираясь на результаты этих исследований, Г. Гримм и В. М. Гольдшмидт дали более широкое определение понятия изоморфизма:
изоморфными являются вещества аналогичной кристаллической структуры. которая определяется одинаковым численным соотношением различных частиц, образующих кристалл, близким соотношением размеров и сходствам поляризационных свойств частиц, а также однотипностью связи.
Эти исследователи сформулировали основные правила изоморфизма, определяющие роль размеров сокристаллизующихся частц при процессах изоморфного замещения, а также предложили классификацию различных типов изоморфизма.
По классификации
Гольдшмидта, существует три рода
изоморфизма. Изоморфизм I рода требует
постоянства суммы зарядов и одинакового
их распределения по отдельным частицам
в обоих веществах и соответствует
изоморфизму по Митчерлиху, например
![]()
Изоморфизм II рода также
требует постоянства суммы зарядов, но
их распределение по частицам может быть
различным, например
![]() .
.
Изоморфизм III рода имеет
место при одинаковом количественном
соотношении частиц, образующих кристалл,
но сумма их зарядов может быть различной,
например
 .
.
Принципиальное различие между изоморфизмом I рода, с одной стороны, и II и III рода, с другой стороны, было установлено В. Г. Хлопиным и Б. А. Никитиным. Это различие состоит в существовании нижней границы смешиваемости в системах, отвечающих условиям изоморфизма II и III рода.
Согласно современным представлениям понятие изоморфизма можно определить следующим образом:
изоморфизмом называется свойство элементов замещать друг друга в кристаллической структуре при условии близости размеров и характера химической связи составляющих кристалл структурных единиц (атомов, простых и сложных ионов, молекул).
Различают изовалентное и гетеровалентное изоморфное замещение. Изовалентный изоморфизм состоит во взаимозамещении одинаково заряженных ионов разных химических элементов в эквивалентных позициях в данной кристаллографической системе. Изовалентное замещение включает в себя собственно изоморфизм (изоморфизм I рода) и изодиморфизм.
Изодиморфизм (принудительный изоморфизм) — явление изоморфной сокристаллизации компонентов, обладающих различными кристаллическими структурами. При этом микрокомгюнент входит в кристаллическую решетку, свойственную макрокомпоненту. В качестве примера изодиморфизма можно привести сокристаллизацию микроколичеств свинца с хлоридом бария, хотя хлорид бария BaCl22H2O кристаллизуется в моноклинной системе, а безводный хлорид свинца—в ромбической. В случае изодиморфизма смешиваемость обоих компонентов ограничена, т. е. существует верхняя граница смешиваемости.
Изовалентный изоморфизм не сопровождается изменением общего числа частиц в кристаллической структуре. На этом виде изоморфизма основаны процессы соосаждения со специфическими носителями.
Гетеровалентный изоморфизм представляет собой взаимозамещение неодинаково заряженных ионов разных элементов. Гегеровалентное замещение может происходить как без изменения, так и с изменением числа частиц в кристаллической структуре при обязательном условии баланса (или компенсации) зарядов.
С процессами гетеровалентного замещения связано образование так называемых аномальных смешанных кристаллов и кристаллов Гримма, которые будут рассмотрены ниже.
Причиной образования изоморфных смесей, назависимо от характера изоморфизма, является стремление системы достигнуть более устойчивого состояния, характеризуемого минимумом свободной энергии.
Рассмотрим основные положения одной из наиболее распространенных теорий изоморфизма, развитой советским исследователем В. С. Урусовым* . Исходным моментом этой теории является общееположение, что возможность образования изоморфной смеси определяется изменением свободной энергии Гиббса:
G - H - TS - U + pV - TS. где H = U + pV и S — соответствующие изменения энтальпии и энтропии системы; U — изменение внутренней энергии системы; V — изменение объема системы.
Для изоморфной смеси состава x1 молярных долей первого компонента и х2 молярных долей второго компонента имеем:
Gсм(x1,x2T) = Gтв.р-р(x1,x2) - x1G1 - x2G2 = Hсм - TSсм, |
(5.2) |
где Hсм и Sсм — соответственно теплота и энтропия смешения.
В соответствии с уравнением (5.2) возможность изоморфного замещения, определяемая знаком и величиной изменения свободной энергии, зависит от соотношения значений теплоты и энтропии смешения.
Теплота смешения Hсм — разность между энтальпиями 1 моль твердого раствора данного состава и суммой энтальпий образующих этот раствор чистых компонентов, взятых в тех же количествах.
В простейшем случае образования твердых регулярных растворов, в которых распределение замещающих друг друга частиц является статистическим, энтропия смешения может быть рассчитана как энтропия смесей с помощью уравнения
Sсм = -R(x1 ln x1 + x2 ln x2). где R — универсальная газовая постоянная. Поэтому основная задача энергетической теории сводится к оценке теплоты смешения. Согласно Урусову, наиболее пригодным способом ее расчета является определение разности энергий атомизации твердого раствора данного состава (Етв. р-р) и чистых компонентов, взятых в тех же количествах. (E1 и Е2):
Hсм(x1, x2) = Eтв. р-р - (x1E1 + x2E2).
Энергия атомизации может быть представлена в виде суммы E = Eи + Eк + E + Eв, где Еи и Ек — соответственно эффективная ионная и ковалентная составляющие энергии связи; E — энергия переноса заряда от электроотрицательного к электроположительному атому; Ев — энергия, обусловленная силами Ван-дер-Ваальса. Величина Еи определяется для кристалла типа АХ выражением
 где
А и , — значения
истинной и приведенной константы
Маделунга; d — межатомное расстояние;
rA и rX — ионные радиусы;
— степень ионности химической связи в
кристалле; n — число атомов в молекуле;
z — формальный ионный заряд; z
— эффективный заряд атома в кристалле.
где
А и , — значения
истинной и приведенной константы
Маделунга; d — межатомное расстояние;
rA и rX — ионные радиусы;
— степень ионности химической связи в
кристалле; n — число атомов в молекуле;
z — формальный ионный заряд; z
— эффективный заряд атома в кристалле.
С учетом правила Вегарда для изменения межионных расстояний с составом раствора
d = x1d1 + x2d2 = d1 + x2d = d2 - x1d, где d = d1 — d2 при d2 < d1, и правила аддитивности характера химической связи, предложенного Урусовым,
= x11 + x22 = 1 + x22 = 2 - x11, где = 2 — 1, было получено следующее выражение для расчета теплоты смешения изоморфной смеси:
Hсм = x1x2 [a(r)2 + b()2], |
(5.3) |
где r — разность радиусов замещающих частиц; — различие в характере химической связи компонентов; а, b— некоторые параметры (положительные числа).
Выражение в квадратных скобках: Q = a(r)2 + b()2 - получило название энергии смешения.
Выражение (5.3) представляет собой основной результат энергетической теории. Как отмечает сам автор, развитая им теория является лишь первым приближением к решению очень сложной проблемы взаимодействия частиц в изоморфных смесях различной природы. Тем не менее энергетическая теория позволяет объяснить установленные ранее эмпирические критерии, определяющие возможность образования изоморфных смесей.
Одним из наиболее известных эмпирических правил изоморфизма является правило Гольдшмидта, устанавливающее максимальную возможность различия в радиусах взаимозамещаемых структурных единиц (10—15% относительно меньшего). В последнее время наблюдается тенденция к замене радиусов взаимозамещаемых частиц на межатомные расстояния, которые могут быть определены экспериментально с большой точностью. В этом случае
|
(5.4) |
где r — радиус общей структурной единицы.
Из выражений (5.3) и (5.4), если пренебречь различиями в характере химических связей компонентов, следует, что чем больше r, тем меньше d/d и Hсм для данной пары элементов и, следовательно, шире пределы изоморфных замещений. Отсюда становится понятным влияние состава соединения на пределы изоморфного замещения. Так, в случае изоморфного замещения катионов пределы смешения тем шире, чем больше размер аниона. Например, пределы замещения лития на натрий для системы LiMnPO4 — NaMnPO4 значительно шире, чем для системы LiCl — NaCl.
Влияние характера химической связи смешивающихся компонентов на пределы изоморфного замещения учитывается вторым членом уравнения (5.3). Как видно из этого уравнения, при близких размерах замещающихся частиц (d/d —> 0) энергия смешения быстро растет с увеличением различий в характере химической связи (), чем и объясняется резкое уменьшение пределов изоморфного замещения. Приближенной мерой служит разность электроотрицательностей Таким образом, большое различие электроотрицательностей замещающих друг друга частиц приводит к резкому уменьшению пределов изоморфной смесимости, несмотря на близость размеров этих частиц.
Классическим примером влияния характера химических связей могут служить системы, включающие хлориды натрия и меди (+1), для которых d —> 0, a 0,9, что соответствует~30%-ному различию в степени ионности химической связи по Полингу. Такое сильное различие электроотрицательностей является причиной экспериментально установленного отсутствия изоморфной смесимости указанных соединений. Таким образом:
основными факторами, определяющими возможность изоморфной смесимости, являются близость размеров замещающих частиц и характер их химической связи, а отсюда — совпадение координационных чисел, а следовательно, и кристаллических структур соединений сокристаллизующихся компонентов.
Рассмотрим закономерности процесса соосаждения со специфическими носителями. Количественной характеристикой процесса соосаждения радиоактивного элемента является равновесная константа распределения.
В общем случае для систем, в которых протекают химические реакции или происходят межфазовые переходы, свободная энергия является функцией температуры, давления и числа молей веществ, участвующих в процессе: G = F(Т, р, n1, n2, ... ,ni). Таким образом,
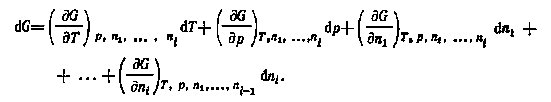
При условии достижения равновесия и постоянства температуры и давления имеем
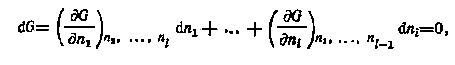
где частные производные представляют собой химические потенциалы соответствующих компонентов:
![]()
Тогда
1dn1 + 2dn2 + ... +idni = 0
Процесс соосаждения со специфическими носителями является межфазным переходом радиоактивного элемента из раствора в кристаллическую фазу. Для этого процесса
dGi = dGl + dGi.
Здесь и далее индекс i соответствует радиоактивному элементу (черта над символом указывает, что данная характеристика относится к твердой фазе).
При равновесии имеем
dGl + dGi = idni + idni = idni - idni = 0, где dni = —dni — количество радиоактивного элемента, перешедшее из одной фазы в другую.
Таким образом, условием термодинамического равновесия в данном случае является равенство химических потенциалов микрокомпонента в твердой и жидкой фазах:
i = i |
(5.5) |
Химические потенциалы распределяющегося компонента в твердой и жидкой фазах могут быть представлены следующим образом:
i = i + RT ln ai, |
(5.6) |
i = i + RT ln ai, |
(5.7) |
где i и i — стандартные химические потенциалы радиоактивного элемента в твердой и жидкой фазах; аi = mii и а = mii— термодинамические активности; mi и mi — концентрации; i и i — коэффициенты активности.
Из уравнений (5.5) — (5.7) следует:
|
(5.8) |
где КN - равновесная термодинамическая константа распределения элемента между твердой фазой и раствором.
Уравнение (5.8) является основным соотношением, описывающим распределение радиоактивного элемента между кристаллической и -жидкой фазами при условии изоморфизма (изодиморфизма) соединений радиоактивного элемента и носителя независимо от концентрации распределяющегося элемента.
Практическое использование соотношения (5.8) затруднено ввиду необходимости определения коэффициентов активности распределяющегося компонента в равновесных фазах.
Для радиохимических исследований наибольшее значение имеют процессы соосаждения микроколичеств вещества со специфическими носителями, когда присутствие распределяющегося элемента практически не оказывает влияния на термодинамические свойства фаз. Для таких систем равновесная твердая фаза является крайне разбавленным идеальным твердым раствором микрокомпонента ( i = 1). Равновесная жидкая фаза представляет собой насыщенный раствор соединения носителя, содержащий микроколичества радиоактивного элемента. В таком растворе коэффициент активности распределяющегося радиоактивного элемента не равен единице. Он определяется значением ионной силы раствора, обусловленной всеми присутствующими в растворе ионами, и остается неизменным в широком интервале концентраций радиоактивного элемента (от предельно малых значений до 10-3 моль/л). Это объясняется тем, что для указанного интервала концентраций присутствие радиоактивного элемента не сказывается на значении ионной силы раствора.
Действительно, при изменяющихся исходных концентрациях радиоактивного элемента mi,0 < mi,0 < mi,0 ... < 10-3 моль/л и наличии равновесия имеем:
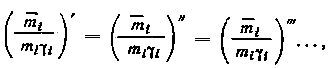 где
i = i
= i = ...
=i = const. Тогда
где
i = i
= i = ...
=i = const. Тогда
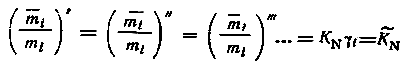 или
или
|
(5.9) |
где КN, — равновесная концентрационная константа распределения.
Использование в качестве объектов исследования микроколичеств радиоактивных элементов позволяет обеспечить неизменность состава и термодинамических свойств фаз.
Применимость соотношения (5.9) к процессам распределения радиоактивных элементов между кристаллами и жидкой фазой была доказана В. Г. Хлопиным и его школой**. Основной заслугой В. Г. Хлопина является доказательство возможности достижения истинного термодинамического равновесия для процессов распределения вещества между кристаллической и жидкой фазами. С этой целью были разработаны специальные экспериментальные приемы, обеспечивающие быстрое установление равновесия, которое в данном случае не может быть достигнуто с помощью процессов конвекции и диффузии. Механизмом, обеспечивающим установление такого равновесия, как показал В. Г. Хлопин, являются процессы многократной перекристаллизации. Физической причиной перекристаллизации служит различие термодинамических свойств кристаллов, отличающихся по размерам и характеру нарушений кристаллической решетки. Вследствие неодинаковой растворимости кристаллических частиц в полидисперсных системах последние не находятся в устойчивом равновесии. Равновесие достигается путем перекристаллизации, переводящей полидисперсную систему в монодисперсную.
Для экспериментального осуществления истинного термодинамического равновесия между кристаллической фазой и раствором В. Г. Хлопин использовал несколько путей.
Первый из них заключался в длительной многократной перекристаллизации вещества носителя в его насыщенном растворе, содержащем радиоактивный элемент, при энергичном перемешивании и при постоянной температуре. Это позволяет Проследить за ходом установления равновесия «снизу».
Второй путь — многократная перекристаллизация заранее приготовленных смешанных кристаллов носителя и радиоактивного элемента в насыщенном растворе носителя при постоянной температуре и энергичном перемешивании (установление равновесия «сверху»). В условиях энергичного перемешивания непрерывно возникающие повреждения кристаллов и образование при этом неоднородных по размерам и форме кристаллических фрагментов делают процесс перекристаллизации бесконечным. При этом происходит как бы перемешивание в кристаллической фазе, в результате чего она оказывается в конце концов в равновесии с жидкой фазой.
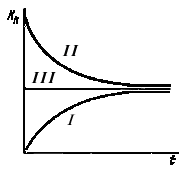
|
Рис. 4. Пути достижения равновесия по Хлопину: I—путь «снизу»; II—путь «сверху»; III—перекристаллизации из пересыщенного раствора |
При образовании кристаллов из сильно пересыщенных растворов число первоначально возникших кристаллических центров во много раз превосходит число выросших впоследствии кристаллов. Таким образом, росту кристаллов предшествует образование большого числа зародышей, которые успевают многократно перекристаллпзоваться и таким путем гомогенизироваться. Образование твердой фазы происходит путем срастания отдельных однородных кристаллов.
Рассмотренные способы достижения равновесия были проверены на большом числе систем, включающих соли бария и радия. На рис. 4 представлены результаты экспериментального изучения системы ВаВr2 — RaBr2 — H2O при температуре 25° С. Как видно из рисунка, все три пути приводят к устойчивому равновесному состоянию, характеризуемому определенным значением КN. При выделении твердой фазы из пересыщенного раствора (III путь) перекристаллизация идет настолько быстро, что равновесие успевает установиться уже в процессе образования твердой фазы.
На основании этих исследований В. Г. Хлопин сформулировал закон распределения (закон Хлопина):
при наличии изоморфизма между веществами носителя и радиоактивного элемента, присутствующего в системе в концентрации, не превышающей 10-3 моль/л, отношение концентраций радиоактивного элемента в равновесных фазах является постоянной величиной, не зависящей от количества выделяемой твердой фазы.
Соотношение (5.9) выражает отношение концентраций радиоактивного элемента в жидкой и твердой фазах, но не отражает изменения соотношений между количествами радиоактивного элемента и специфического носителя в этих фазах. Поэтому для представления экспериментальных данных по распределению радиоактивных элементов между фазами более удобна формула, предложенная Л. Гендерсоном и Ф. Kрэчеком:
|
(5.10) |
где х = miV—масса радиоактивного элемента, перешедшего в твердую фазу; у = mnV — масса специфического носителя, перешедшего в твердую фазу: а—х = miV—масса радиоактивного элемента, оставшегося в жидкой фазе; b — у = mnV — масса специфического носителя в жидкой фазе; а и b — общее содержание веществ радиоактивного элемента и специфического носителя; mi и mi; — равновесные концентрации радиоактивного элемента в кристаллической и жидкой фазах; mn и mn — равновесные концентрации специфического носителя в кристаллической и жидкой фазах; V и V — объемы этих фаз; D — коэффициент кристаллизации (константа фракционирования).
В соответствии с принятыми нами обозначениями формула (5.10) может быть представлена следующим образом:

или
|
(5.11) |
Коэффициент кристаллизации показывает, во сколько раз отношение между количествами радиоактивного элемента и специфического носителя в твердой фазе больше (D > 1) или меньше (D < 1) аналогичного отношения в жидкой фазе.
Легко показать, что для систем, разбавленных в отношении радиоактивного элемента,
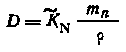 ,
где
—плотность твердой
фазы. Действительно, выражение (5.11) можно
представить в виде
,
где
—плотность твердой
фазы. Действительно, выражение (5.11) можно
представить в виде
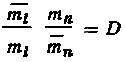 ,
где
,
где
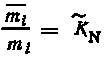 при
mn = .
при
mn = .
Насколько строго распределение радиоактивного элемента подчиняется закону Хлопина, видно из результатов исследования системы BaCl2 — RaCl2 — H2O, проведенного в лабораториях разных стран (табл. 1).
Т а б л и ц а 1. Распределение радия между кристаллами и раствором BaCl2 (при 0° C) |
|||||
По данным В.Г.Хлопина |
По данным О.Гана |
||||
Осажденный BaCl2,% |
Захваченный RaCl2, % |
D |
Осажденный BaCl2,% |
Захваченный RaCl2, % |
D |
6,49 |
26,56 |
5,21 |
2,52 |
12,59 |
5,58 |
12,95 |
44,15 |
5,31 |
6,91 |
28,08 |
5,28 |
15,13 |
47,72 |
5,12 |
10,79 |
39,70 |
5,44 |
22,71 |
61,35 |
5,40 |
11,55 |
40,99 |
5,32 |
28,75 |
68,44 |
5,31 |
11,61 |
49,91 |
5,27 |
32,70 |
72,27 |
5,36 |
13,42 |
45,38 |
5,36 |
- |
- |
- |
16,47 |
52,39 |
5,58 |
50,98 |
85,62 |
5,73 |
17,04 |
51,60 |
5,19 |
76,90 |
94,45 |
5,68 |
19,76 |
56,85 |
5,35 |
- |
Среднее 5,36 |
- |
Среднее 5,35 |
||
См.: Урусов В. С. Теория изоморфной смесимости. М., Наука, 1977. ** См.: Хлопин В. Г. Избранные труды. М., Изд-во АН СССР, 1956.