
- •В.Д.Нефедов е.Н.Текстер м.А.Торопова радиохимия
- •Глава 1
- •§ 1. Предмет радиохимии
- •§ 2. Краткий очерк истории развития радиохимии
- •§ 3. Особенности радиохимии
- •§ 4. Значение радиохимии
- •1 Общая радиохимия глава 2
- •§ 1. Общехимические свойства изотопных частиц
- •2. Термодинамическое поведение изотопных частиц
- •3. Кинетическое поведение изотопных частиц
- •Глава 3
- •§ 1. Классификация реакций изотопного обмена
- •§ 2. Причины протекания реакций изотопного обмена
- •3. Особенности реакций идеального изотопного обмена
- •§ 4. Основное уравнение кинетики реакций идеального изотопного обмена
- •§ 5. Основы экспериментальных методов исследования процессов изотопного обмена
- •Глава 4
- •§ 1. Состояние радиоактивных элементов [нуклидов] в жидкой фазе
- •§ 2. Процессы радиоколлоидообразования
- •§ 3. Основы экспериментальных методов исследования радиоколлоидов
- •Глава 5
- •§ 1. Закономерности процессов соосаждения с изотопными носителями
- •§ 2. Основные области применения изотопных носителей
- •§ 3. Принцип действия и закономерности процессов соосаждения со специфическими носителями
- •§ 4 Факторы, влияющие на процесс соосаждения со специфическими носителями
- •§ 5. Особенности процессов соосаждения со специфическими носителями
- •§ 6. Сокристаллизация со специфическими носителями при отсутствии изоморфизма 1 рода
- •§ 7. Основы экспериментальных методов исследования процессов соосаждения со специфическими носителями
- •§ 8. Основные области применения специфических носителей
- •Глава 6
- •§ 1. Первичная адсорбция
- •§ 2. Вторичная обменная адсорбция
- •§ 3. Закономерности процесса соосаждения с неспецифическими носителями
- •§ 4. Соосаждение с неспецифическими носителями при образовании внутренне-адсорбционных систем
- •§ 5. Основы экспериментальных методов исследования процессов соосаждения с неспецифическими носителями
- •§ 6. Основные области применения неспецифических носителей
- •§ 7. Методы разграничения различных видов соосаждения
- •Глава 7
- •§ 1. Закономерности и классификация экстракционных процессов
- •§ 3. Практическое использование процессов экстракции
- •Глава 8
- •§ 1. Основные закономерности хроматографических процессов Ионообменная хроматография.
- •Распределительная хроматография.
- •См.: Егоров е. В., Макарова с. Б. Ионный обмен в радиохимии. М., Атомиздат, 1971. § 2. Основы экспериментальных методов хроматографического исследования
- •См.: Роберте т. Радиохроматография. М., Мир, 1981. § 3. Примеры практического использования хроматографических методов в радиохимии
- •Глава 9
- •§ 1. Закономерности электрохимических процессов
- •§ 2 Особенности поведения радиоактивных элементов (нуклидов) при электрохимических процессах
- •§ 3. Основы экспериментальных методов исследования электрохимических процессов
- •§ 4. Использование электрохимических процессов в радиохимии
- •2 Химия радиоактивных элементов
- •Глава 10
- •§ 1. Технеций
- •§ 2. Прометий
- •§ 3. Полоний
- •§ 4. Астат
- •§ 5. Радон
- •§ 6. Франций
- •§ 7. Радий
- •Глава 11
- •§ 1. История открытия актиния и актиноидов
- •§ 2. Важнейшие изотопы актиния и актиноидов, методы их получения и идентификации
- •§ 3. Физические свойства актиния и актиноидов
- •§ 4. Актиний
- •§ 5. Торий
- •§ 6. Протактиний
- •§ 7. Уран, нептуний, плутоний и америций
- •§ 8. Трайсамерициевые актиноиды
- •Глава 12
- •§ 1. История открытия
- •§ 2 Методы получения и идентификации
- •3 Химические последствия радиоактивного распада
- •Глава 13
- •§ 1. История открытия ядерной изомерии
- •§ 2. Особенности явления ядерной изомерии
- •§ 3. Химические последствия изомерных переходов
- •§ 4. Практическое использование химических последствий изомерного перехода
- •Глава 14
- •§ 1. Теоретические аспекты химических последствий --распада
- •§ 2. Экспериментальные методы исследования химических последствий --распада
- •§ 3. Практическое использование химических последствий --распада
§ 2. Причины протекания реакций изотопного обмена
Вопрос о причинах протекания процессов идеального изотопного обмена не тривиален, поскольку в данном случае мы имеем дело с процессами перемещения частиц, тождественных по своим свойствам.
Предположим, что самопроизвольный процесс изотопного обмена
AX + BX* AX* + BX |
(IV) |
протекает в идеальной закрытой системе при постоянных температуре и давлении. Известно, что в изобарно-изотермических условиях могут протекать лишь процессы, приводящие к уменьшению изобарно-изотермического потенциала (свободной энергии Гиббса).
Обозначим через G1, G2, ...,Gk и т. д. значения свободных энергий системы в различные моменты времени t1, t2, ..., tk протекания процесса обмена (tk—время достижения равновесия системы). Очевидно, что G1 > G2 > ... > Gk. Поскольку G = H — TS, то
(H1 - TS1) > (H2 - TS2) > (Hk - TSk) |
(3.1) |
Изменение энтальпии системы в результате реакции (IV) может происходить за счет энергетических изменений вследствие разрушения начальных и образования конечных связей:
a) AX A + X - H1 б) BX* B + X* - H2 в) A + X* AX* + H1 г) B + X BX + H2
Энтальпии реакций (а), (в) и (б), (г) равны и противоположны по знаку, поскольку энергии связей изотопных атомов совпадают. Тогда для реакции (IV)
H = Hкон - Hнач = (H1 + H2) - (H1 + H2) = 0.
Таким образом, для реакции идеального изотопного обмена изменение энтальпии системы равно нулю, и неравенство (3.1) может быть записано следующим образом:
TS1 < TS2 < ... < TSk или S1 < S2 < ... < Sk.
Это означает, что причиной протекания самопроизвольных процессов идеального изотопного обмена является у в е л и ч е н и е э н т р о п и и с и с т е м ы. При этом уменьшение свободной энергии при переходе от начального к конечному состоянию
G = Gk - G1 = -TSk + TS1 = -TG. |
(3.2) |
С физической точки зрения увеличение энтропии при изотопном обмене соответствует переходу системы из более упорядоченного состояния (каждый изотоп находится в составе определенной химической формы) к менее упорядоченному (каждый изотоп распределен между обеими обменивающимися формами, что соответствует смешению изотопов).
Для расчета S необходимо найти изменение свободной энергии системы в результате изотопного обмена. В общем случае это можно сделать, рассматривая процесс обмена либо как перераспределение изотопов между различными химическими формами AX1, ВХ2, ..., YXi, взятыми в соответствующем числе молей n1, n2, ..., ni:
n1AX1 + n2BX2 + niYXi n1A (X1, X2, ... Xi) + n2B (X1, X2, ... Xi) + ... +niY (X1, X2, ... Xi)
либо как процесс непосредственного смешения n1, n2, ..., ni молей атомов изотопов X1, Х2, ..., Хi, находящихся в объемах V1, V2, ..., Vi путем удаления перегородок, разделяющих эти объемы. При изотопном обмене роль таких перегородок играет нахождение каждого изотопа в определенной химической форме:
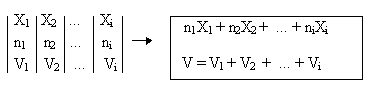
Выражая начальные и конечные значения свободной энергии системы с помощью статистических сумм, имеем: а) для свободной энергии системы до смешения

где Q — полная статистическая сумма; Qвн — частная статистическая сумма, связанная с внутренними степенями свободы движения, при постоянных давлении и температуре остается неизменной; б) для свободной энергии системы после смешения
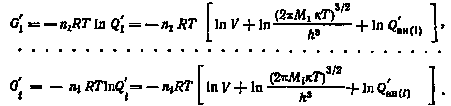
Суммируя конечные и начальные значения свободной энергии изотопных компонентов и беря разность этих сумм, получим

где Ni — молярная доля изотопа после смешения. Учитывая, что G = —TS, получим S = — . Поскольку Ni всегда меньше единицы, то S является положительной величиной.
