28.Критерий согласия. Критерий (Пирсона).

Пусть имеется теор.закон распр. р1,р2..рn Значения х1,х2..хnсгрупированны по m интервалам. Есть выборка объёма n: n1,n2..nm;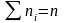 Пусть проверяется гип.о выбранном виде закона распр.с.в.1.Расчитывается мера расхождения между наблюденными частотами и теор. Частотами x2по фор-ле:

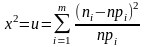
2.Д/данного уровня значимости α по табл. Х2-распр.нах-ся крит.знач.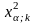 при числе степеней свободы k=m-r-1

3.Если х2> то гип.Н0 отвергается, а если х2≤ то нет основания отказываться от теор.закона распр.

29 Линейное однофакторное уравнение регрессии.

Предполагается, что для оценки параметров регрессии взята выборка, содержащая n-параметров значения.Оценкой уравнения регрессии является выборочное уравнение, где параметры а0 и а1 являются точечными оценками соответствия параметров исходного уравнения и могут быть найдены методом наименьшего квадрата.Метод наименьшего квадрата-это нахождение параметра модели, при котором минимизируется сумма квадрата отклонения эмпирического значения от теоретического, полученного по выборочному уравнению регрессии.Регрессионную модель удобно представлять графически. Но по графику можно только приблизительно сделать вывод о качестве модели.Существуют способы более точной оценки адекватности. Проверить значимость, значит установить соответствует ли математическая модель, выражающая зависимость между переменными.

Для проверки значимости уравнения регрессии на уровне значимости вычисляют наблюдаемое значение случайной величины.

30. Линейное многофакторное уравнение регрессии.Линейное многофакторное уравнения регрессии имеет вид  , где a, b1, bn параметры; x1, xn экзогенные переменные; y эндогенная переменная. 

31.Схема однофакторного дисперсионного анализа.

Однофакторная дисперсионная модель имеет вид:  xij = μ + Fj + εij, (1) где хij – значение исследуемой переменой, полученной на i-м уровне фактора (i=1,2,...,т) c j-м порядковым номером (j=1,2,...,n); Fi – эффект, обусловленный влиянием i-го уровня фактора;  εij – случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариацией переменой внутри отдельного уровня. Основные предпосылки дисперсионного анализа: - математическое ожидание возмущения εij равно нулю для любых i, т.е. M(εij) = 0; (2) - возмущения εij взаимно независимы;

- дисперсия переменной xij (или возмущения εij) постоянна для любых i, j, т.е. D(εij) = σ2; (3) - переменная xij (или возмущение εij) имеет нормальный закон распределения N(0;σ2).

1.сущность и условия применения теорий вероятностей

2. Основные понятия теорий вероятностей: событие и элементарные исходы события.

3.Классичиское, статистическое и геометрическое определение вероятностей.

4. теоремы сложения и умножения вероятностей.

5.Теорема о вероятности хотя бы одного события.

6. формула полной вероятности. Теорема Байеса.

7.Повторные испытания. Формула Бернулли.

8.Случайные величины, способ их описания.

9 основные числовые характеристики дискретных случайных величин.

10.Основные числовые характеристики непрерывных случайных величин.

11.Равновероятностный закон распределения распределениявероятностей и его характеристики.

12. Биномиальный закон распределения вероятностей и его характеристики .

13. Закон распределения вероятностей Пуассона и его характеристики.

14.Нормальные закон распределения вероятностей и его характеристики.

15.Экспонециальный закон распределения вероятностей . Функция надежности.

16.Центральна предельная теорема. Теорема Ляпунова.

17. задачи математической статистики.

18. способы отбора данных. Генеральная и выборочная совокупность.

19.статистическое оценивание параметров дискретных случайных величин. Выборочная средняя и выборочная Дисперсия.

20. статистическое оценивание параметров непрерывных случайных величин. Выборочная средняя и выборочная Дисперсия

21статистическе оценивание:метод моментов, метод максимального правдоподобия.

22интервальные оценки для параметров нормального закона распределения.

23. статистические оценки параметров распределения. Несмещенность, состоятельность, эффективность и надежность оценки.

24. статистическая гипотеза. Нулевая гипотеза. Ошибки первого и второго рода.

25. проверка статистической гипотезы о равенстве средних значений.

26.проверка статистической гипотезы об однородности дисперсий.

27.проверка статистической гипотезы о статистической взаимосвязи.

28.Критерий согласия. Критерий X2(Пирсона)

29. линейное однофакторное управление регрессии.

30. Линейное многофакторное управление регрессии.

31.схема однофакторного дисперсионного анлазиза.