1.Сущность и условия применения теории вероятностей.

Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Методы теории вероятности по природе приспособлены только для исследования массовых случайных явлений; они не дают возможность предсказать исход отдельного случайного явления, но дают возможность предсказать средний суммарный результат массы однородных случайных явлений.

Т.в. служит для обоснования математической и прикладной статистики, которая используется при планировании организации производства и др.

2.Основные понятия теории вероятностей: событие и элементарные исходы события.

Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Методы теории вероятности по природе приспособлены только для исследования массовых случайных явлений; они не дают возможность предсказать исход отдельного случайного явления, но дают возможность предсказать средний суммарный результат массы однородных случайных явлений.

В теории вероятностей испытанием принято называть эксперимент, который (хотя бы теоретически) может быть произведён в одних и тех же условиях неограниченное число раз.

Результат или исход каждого испытания назовём событием. Событие являетсяосновным понятием теории вероятностей. Будем обозначать события буквами А, В, С.

Виды событий:

достоверное событие - событие, которое в результате опыта обязательно произойдет.

невозможное событие - событие, которое в результате опыта не может произойти.

случайное событие - событие, которое может произойти в данном опыте, а может и не произойти.Равновозможность событий означает, что нет оснований предпочесть какое-либо одно из них другим.

Вероятностьюсобытия A (обозначают P(A)) называется отношение числа исходов, благоприятных событию A (обозначают m(A)), к числу всех исходов испытания – N т.е. P(A)= m(A)/ N.

4.Теоремы сложения и умножения вероятностей

Е 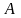сли А и В несовместны, то Р(А + В) = Р(А) +Р(В)

Если и противоположные события, то

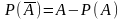
Если А и В совместны, то теорема сложения принимает вид:

Р(А+В)=Р(А)+Р(В) - Р(АВ).

Теоремы умножения вероятностей.

Если А и В независимые события, то

Р(АВ) = Р(А)*Р(В).

Если А и В совместны, то

P(A*B)=P(A)*P(B/A)

5.Теорема о вероятности хотя бы одного события

Вероятность появления хотя бы одного из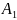 , …. независимых в совокупности равна разности между единицей и произведением вероятностей противоположных событий: , …

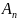
P(A)=1- …. 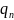, где =P( )

=1- , i=1,2,….n

П усть событие А может наступить при условии реализации одной из гипотез Н1, Н2, ..., Нn, образующих полную группу событий. Тогда

Формула (1) называется формулой полной вероятности.