6. Корреляционно-регрессионный анализ

Рассматривая зависимости между признаками, необходимо выделить, прежде всего, две категории зависимости: 1) функциональные и 2) корреляционные.

Функциональные связи характеризуются полным соответствием между изменением факторного признака и изменением результативной величины, и каждому значению признака-фактора соответствуют вполне определенные значения результативного признака.

В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных.

Корреляционный анализ позволяет количественно оценить связи между большим числом взаимодействующих экономических явлений как между случайными величинами или группой величин. Корреляционный анализ тесно связан с регрессионным анализом, задача которого состоит в экспериментальном определении параметров корреляционных зависимостей между экономическими показателями путем наблюдений за характером их изменений. Одним из основных методов определения параметров регрессионных уравнений в рамках регрессионного анализа является метод наименьших квадратов. Модели, составленные с помощью применения регрессионного анализа, позволяют прогнозировать варианты развития экономических явлений и процессов и изучать тенденции изменения экономических показателей.

Парная регрессия и корреляция

1. Парная линейная регрессия

2. Поле корреляции

3. Ошибки, встречающиеся при эконометрических исследованиях

4. Метод наименьших квадратов

5. Вычисление пара метров регрессии и их интерпретация

6. Вычисление коэффициента корреляции и детерминации, их интерпретация.

7. Критерий Фишера.

8. Стандартные ошибки параметров.

9. Критерии Стьюдента.

10. Ошибки аппроксимации.

11. Прогнозирование в линейной регрессии.

1.Парная регрессия

В парной линейной регрессии связь между переменными определяется следующим образом:

Построение линейной регрессии сводится к оценке ее параметров – и .

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности в целом наблюдаемых данных. Так, если зависимость потребления электроэнергии у от объема выпускаемой продукции х можно представить в следующем виде: у = 1500 + 24,8х , то это оз­начает, что при увеличении объема выпуска на 1 ед. потребле­ние электроэнергии в среднем возрастает на 24,8 ед. Таким образом, в уравнении регрессии связь между результатом и фактором представляется в качестве функциональной, причем функция, определяющая вид уравнения регрессии, мо­жет быть не только линейной.

2.Поле корреляции.

Каждую пару наблюдений x_i ,y_i можно представить в виде точки на плоскости ху. Такое графическое построение называется полем корреляции. В этом случае наилучшей считается функция, график которой проходит через наибольшее количество точек или как можно ближе к ним (рис. 2.1).

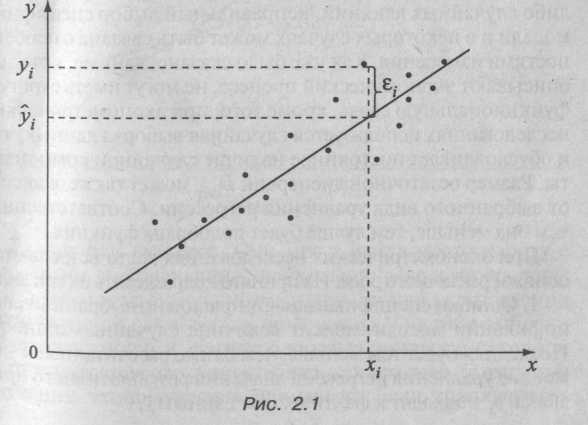
В каждом из наблюдений величину случайной компоненты можно определить как разность между фактическим значением результата и рассчитанным по уравнению регрессии:

В качестве меры отклонений используется сумма квадратов отклонений (остаточная дисперсия D_ост.)э