Описание геометрического развивающего материала
Первая серия вкладышей: квадраты, фигуры, состоящие из отдельных частей.
Эта серия состоит из 9 квадратных вкладышей, в основе которых есть углубления — одинаковые белые квадраты со стороной 10 см. В одно углубление вложен целый квадрат, в другие — те же квадраты, но состоящие из отдельных частей:
– квадрат, состоящий из 2 равных прямоугольников;
– квадрат, состоящий из 4 равных прямоугольников;
– квадрат, состоящий из 8 равных прямоугольников;
– квадрат, состоящий из 16 равных прямоугольников;
– квадрат, состоящий из 2 равных треугольников;
– квадрат, состоящий из 4 равных треугольников;
– квадрат, состоящий из 8 равных треугольников;
– квадрат, состоящий из 16 равных треугольников.
Ребенок может взять квадрат, состоящий из 2 равных прямоугольников, и квадрат, состоящий из 2 равных треугольников, поменять местами части фигур, то есть первый квадрат заполнить двумя треугольниками, а второй — прямоугольниками. Части фигур можно наложить друг на друга внутренней стороной (на внешней будут мешать кнопки, которые нужны для удобства доставания фигуры из рамки). Наложение позволяет установить равенство фигур. Однако треугольник и прямоугольник — разные по форме фигуры, хотя каждая из них составляет ровно половину того же самого квадрата. Так рождается ощущение равенства площади фигур. Два треугольника равны между собой, и два прямоугольника равны между собой. Ученик сравнивает их, накладывая фигуры друг на друга, и замечает, что часть треугольника, выходящая за пределы прямоугольника, равна той части треугольника, которая прикрыта прямоугольником. Следовательно, треугольник и прямоугольник отличаются по форме, но равны по площади.
Аналогичные наблюдения повторяются и с другими квадратами, разделенными на большее количество частей. Квадратики, являющиеся четвертой частью большого квадрата (они получились в результате деления фигуры по медианам), равны между собой и равны по площади треугольникам, возникшим в результате деления большого квадрата по диагоналям. Фигуры, одинаковые по форме, но отличающиеся по размеру, являются подобными. Прямоугольник — половина большого квадрата, подобен прямоугольнику, являющемуся 1/8 большого квадрата, при этом они не равны между собой, у них разная площадь. Также подобны друг другу большой квадрат и маленький, четвертушка большого. И т. д.
В разделении квадрата на части уже содержится идея дроби, хотя это пока еще не тот материал, который специально предназначен для изучения дробей.
Вторая серия вкладышей: дроби.
Десять дощечек с углублениями в форме круга диаметром 10 см, белого цвета. В первое углубление вложен целый круг, в остальные — такие же круги, но поделенные на 2, 3, 4, 5, 6, 7, 8, 9, 10 равных частей. Дети учатся измерять углы каждой части. Для этого мы вырезали картонный круг. Центр обозначен черной точкой на светлом фоне. Очерчен полукруг, радиус которого равен радиусу вкладышей. Этот полукруг поделен лучами на 18 секторов. Лучи выходят за пределы дуги полукруга, сверху написаны числа: 0, 10, 20 — и так до 180. Дуга каждого сектора поделена еще десятью маленькими делениями. Получилась шкала, где одно деление равно одному градусу. Линии, соединяющие 0 и 180 и идущие от центра к 90°, проведены толще, чем остальные, они чуть выпуклые, что позволяет накладывать фигуры точнее. Ученик кладет фигуру вкладыша на картонный расчерченный круг так, что вершина угла совпадает с центром, а одна из сторон заканчивается на нуле. Читаем цифру над окончанием другой стороны фигуры — это и есть величина угла в градусах. После таких упражнений, после работы с транспортиром, ребенок умеет измерять любые углы. Он знает, что круг — это 360°, полукруг — 180°, а прямой угол — 90°.
Теперь можно сосчитать, сколько градусов составляет угол седьмой части круга. 360°: 7=51°, это легко проверить наложением фигуры на расчерченный круг. Подсчеты и измерения можно повторить со всеми вкладышами, составляющими от половины до десятой части круга.
1/3 круга = 120°, 360°: 3-120°,
1/4 круга = 90°, 360°: 4 = 90°, и т. д…
1/10 круга = 36°, 360°: 10 = 36°.
Если знаменатели равны, то сложение дробей происходит путем простого сложения числителей. Знаменатель сохраняется.
Ребенок запоминает дроби: 1/2, 1/3, ... 1/10 У него есть и материальной восприятие, и арифметическое вычисление. С этим материалом можно совершать бесчисленные упражнения, осваивая счет с дробями. К примеру, ученик берет круг, состоящий из двух частей, и заполняет его фигурами — четвертинками круга. Он может оставить одну половину, а вместо второй положить две четвертинки. Вскоре он поймет: 1/2+1/2=1/4+1/4 +1/4+1/4, а две половинки равны четырем четвертям: 2/2 = 4/ 4. Ребенок мысленно считает дроби, видя части круга, и в состоянии выразить свое понимание при помощи математической записи. Наблюдения можно анализировать более глубоко.
1/2+1/2=2/2
1/4+1/4 +1/4+1/4=4/4
1/2+1/2=1/4+1/4 +1/4+1/4
Две половины и четыре четверти — это целый круг. Заполняя круг разными по размеру частями (например, один полукруг и две четверти), ребенок видит соотношение дробных чисел.
1 = 1/2+2/4, то есть 1/2=2/4. То же и с остальными дробями.
Ребенок учится сокращать дроби, видеть их простейшее выражение. Приходит очередь и сложных примеров, которые сначала выполняются при помощи вкладышей, а затем только на бумаге.
Теперь можно переходить и на другие предметы, поддающиеся счету и делению, в частности, на бусины, жетоны, фасолины.
Мы составляем приказания:
– Возьми 1/5 от 25 бусин.
– Возьми 1/4 от 36 жетонов.
– Возьми 1/3 от 27 фасолин.
Бывают приказания, требующие вычислений в два действия, к тому же разными способами:
– Возьми 2/5 от 60 бусин. 60: 5 = 12; 2x12 = 24 или 2x60 = 120;
120: 5 = 24 и т. д.
Преобразование обычных дробей в десятичные: дощечка, напоминающая круглые вкладыши, только фон не светлый, а темный, на нем обозначены деления.
Штрихи подлиннее делят круг на 10 частей, они обозначены цифрами: 0, 10… 90. Штрихи покороче делят каждую дугу пополам, еще более короткие делят каждую половину на пять частей. Получается круг, поделенный на 100 частей. Линия от центра к вершине, над которой стоит 0, (радиус) выпуклая, чтобы точнее расположить фигуры, которые мы хотим измерить.
Чтобы перевести обычную дробь в десятичную, мы берем часть вкладыша, уже измеренную, располагаем ее в нашем круге, совмещая центры и одну из сторон фигуры с выпуклым радиусом. Остальная часть фигуры должна лежать справа от радиуса, в сторону увеличения цифр. Если мы положим так одну четвертую часть круга, то сразу увидим по цифре над окончанием второй стороны фигуры, что 1/4 — 0, 25.
Можно положить рядом, сторона к стороне, несколько фигур-вкладышей и увидеть:
1/3+1/4+1/8= 0,70 (примерно).
Этот материал прекрасно развивает арифметические навыки. Круг (единичное целое) поделен на 100 частей, и мы можем делить эти 100 фрагментов на любое количество долей. Все, что получится, будет сотыми частями целого. 1/4 = 100: 4 = 25 сотых, то есть 25/100 или 0,25. Деление совершается делением числителя на знаменатель: 1:4 = 0,25.
Третья серия вкладышей: равные по площади фигуры.
Этот материал позволяет вычислять площади разных фигур и дает предварительное представление о некоторых геометрических теоремах, которые обычно не изучаются в начальной школе. Считается, что это недоступно пониманию маленьких детей.
Треугольник и прямоугольник равны по площади, если одна сторона прямоугольника равна основанию треугольника, а другая сторона прямоугольника равна половине высоты треугольника.
На широкой прямоугольной рамке есть два белых пространства (две выемки): равные по площади треугольник и прямоугольник.
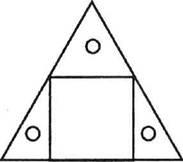
Вкладыши составлены так, что могут заполнить и прямоугольное, и треугольное пространство. Это треугольник, состоящий из трех частей.
Параллельная линия делит высоту треугольника пополам, вертикальная делит верхнюю часть на два равных треугольника. Можно наложить эти маленькие верхние треугольнички друг на друга и убедиться, что они равны.
Работа с бусинами и числовым квадратом научила детей находить площадь квадрата, умножая одну сторону на другую. Площадь прямоугольника также равна произведению смежных сторон. Работая с вкладышами, ребенок видит, что треугольник превращается в прямоугольник. Значит, их площади равны. Следовательно, площадь треугольника равна произведению его основания на половину высоты.
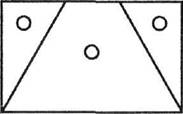
Равны площади ромба и прямоугольника, если одна сторона прямоугольника равна стороне ромба, а вторая — высоте ромба.
Вкладыши состоят из ромба, разделенного диагональю на два равных треугольника, и прямоугольника, разделенного на три треугольника таким образом, что они могут заполнить и ромбовидное пространство рамки, и прямоугольное. В комплект входят и целые фигуры ромба и прямоугольника. Если их наложить друг на друга, можно убедиться, что высоты равны. Равенство площадей фигур доказывается перемещением трех частей прямоугольника в ромбовидное пространство и обратно в прямоугольное. Отсюда следует очевидный вывод, что площадь ромба равна произведению стороны на высоту. (Площадь прямоугольника ребенок уже умеет вычислять.)
Равны площади трапеции и прямоугольника, если одна из сторон прямоугольника равна сумме двух оснований трапеции, а вторая — равна половине высоты трапеции. Ребенок может обнаружить и второй вариант равенства площади трапеции и прямоугольника. Если одна сторона прямоугольника равна высоте трапеции, а вторая — полусумме двух оснований.
Для этого достаточно разделить длинный прямоугольник пополам и положить одну часть над другой, образовав прямоугольник короче и шире первого. Большая прямоугольная рамка содержит три углублунных пространства: два трапецевидных (одинаковых) и одно прямоугольное, равное по площади, чья длина равна сумме двух оснований, а высота — половине высоты трапеции. Вкладыш в одну трапецию состоит из двух частей. Трапеция как бы разрезали по горизонтали на уровне половины высоты. Наложив обе части друг на друга, можно убедиться, что высоты равны. Вторая трапеция разделена на 4 части, которыми можно заполнить и прямоугольное пространство.
Равенство площадей двух фигур очевидно, а значит, можно понять, как вычислить площадь трапеции (умея вычислять площадь прямо-
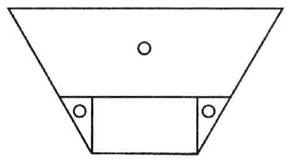
угольника): произведение суммы двух оснований на половину высоты, или произведение полусуммы оснований на высоту. Ученики, измерив стороны фигур, могут произвести арифметические вычисления.
Равны площади правильного многоугольника и прямоугольника, если одна сторона прямоугольника равна периметру многоугольника, а вторая — половине апофемы.
Есть две отдельные рамки с углублениями в форме многоугольника. Один вкладыш представляет собой целый многоугольник, второй — многоугольник, разделенный на треугольники. К примеру, возьмем десятиугольник, значит, и треугольников будет 10. На отдельной рамке — прямоугольное углубление, которое можно заполнить треугольниками, разделенными горизонтальным разрезом на две половинки на уровне половины высоты (два треугольника должны быть еще разделены пополам вертикальным разрезом).
В геометрическом альбоме рисуем таблицу, демонстрирующую равенство площадей десятиугольника и прямоугольника. Рисуем отдельно развертку десятиугольника — 10 треугольников в ряд, горизонтальной пунктирной линией обозначаем уровень половины высоты треугольника. Рядом (параллельно) нужных размеров прямоугольник, а рядом прямоугольник, в который «врисованы» треугольники.
Из 10 треугольников-вкладышей можно без рамки сложить еще один прямоугольник (один треугольник при этом делится еще на два равных треугольничка вертикальным разрезом) и убедиться, что площадь многоугольника равна площади прямоугольника, одна сторона которого равна целой апофеме многоугольника, а другая — половине периметра. Становится понятно, что площадь правильного многоугольника равна произведению периметра на половину апофемы, или произведению апофемы на половину периметра.