5 Тепловое излучение

Основные понятия. Тепловое излучение (радиационный или лучистый теплообмен)- это распространение через газовый слой внутренней энергии излучающего тела путем электромагнитных волн. Возбудителями этих волн являются электрически заряженные частицы, входящие в состав тела. Всякое тело, имеющее температуру ,отличную от абсолютного нуля, способно излучать лучистую энергию, т.е. наряду с потоком энергии от более нагретых тел к менее нагретым всегда имеется и обратный поток энергии от менее нагретых тел к более нагретым. Конечный результат этого обмена и представляет количество теплоты, передаваемой излучением. Наиболее наглядным примером лучистого теплообмена является излучение Землей теплоты от Солнца (солнечная радиация). Существуют различные виды электромагнитного излучения: -излучение, рентгеновское излучение, радиоволны и др. Однако способностью трансформироваться в теплоту (повышать внутреннюю энергию

21

облучаемого тела) обладает излучение светового диапазона (длина волн 0,4-0,8 мкм) и в наибольшей мере инфракрасного диапазона. С увеличением температуры тела тепловое излучение увеличивается, т.к. увеличивается внутренняя энергия тела.

Большинство твердых и жидких тел излучают энергию всех длин волн в интервале от до , т.е. имеют непрерывный спектр излучения. Газы, испускают энергию только в определенном интервале длин волн (селективный спектр излучения). Лучистый поток, излучаемый с единице поверхности тела по всем направлениям полусферического пространства, называется плотностью излучения , Вт/м . Если величина одинакова для всех элементов поверхности , то полный поток , Вт.

Если на тело падает лучистый поток , то часть этого потока будет поглощаться телом, часть - отражаться, а часть - проходить сквозь него: . Поделив это равенство на величину , получим соотношение коэффициентов поглощения , отражения и прозрачности :

. (45)

Для абсолютно черного тела и ; для абсолютно белого тела и ; для абсолютно прозрачных тел и .

Большинство твердых и жидких тел для тепловых лучей практически непрозрачны, т.е. для них и .

Одно- и двухатомные газы практически прозрачны для теплового излечения ( ). Трех- и многоатомные газы обладают селективной способностью излучать и поглощать энергию.

Участвующие в лучистом теплообмене тело (например, твердое),помимо собственного излучения отражает падающую на него энергию в количестве . Сумма энергии собственного отраженного излучения составляет эффективное излучение тела:

. (46)

Для расчета лучистого теплообмена между телами важное значение имеет результирующее излучение, представляющее разность между потоком, получаемым телом, и потоком, которое оно испускает. Плотность результирующего излучения

. (47)

Из (46) и (47) в случае прозрачного газового слоя ( ) имеем

. (48)

Закон теплового излучения. Закон Планка устанавливает зависимость интенсивности излучения от температуры Т и длины волны л: при всех температурах интенсивность излучения равна нулю при .

и , а при некотором промежуточном значении имеет максимум; для всех длин волн интенсивность излучения тем выше, чем выше температура.

Длину волны, которой соответствует максимум теплового излучения, согласно закону Вина, можно найти из условия, (мкм) . Следовательно, с повышением температуры максимум излучения смешивается в сторону более коротких волн.

Согласно закону Стефана–Больцмана, плотность потока собственного излучения абсолютно черного тела (как результат суммирования интенсивности излучения по всем длинам волн) прямо пропорциональна абсолютной температуре тела в четвертой степени:

(49)

где − постоянная излучения абсолютно черного тела ( ). Для практических расчетов это уравнение приводят к виду , где .

Спектры излучения реальных тел отличны от спектра излучения абсолютно черного тела. При этом интенсивность излучения тела на любой длине волны никогда не превышают

22

соответствующую интенсивность излучения абсолютно черного тела. Частным случаем реальных тел являются серые тела, спектр излучения которых подобен спектру излучения черного тела. В практике расчетов с определенной степенью точности реальные тела считают серыми, для которых закон Стефана – Больцмана имеет вид

(50)

где − коэффициент излучения (степень черноты) серого тела; всегда .

Согласно закону Кирхгофа, отношение излучательной способности к поглощательной при температурном равновесии не зависит от природы тела, т.е. поглощательная способность численно равна степени черноты тела: .

C помощью закона Стефана–Больцмана можно определить общее количество энергии, излучаемое телом по всем возможным направлениям. Однако распределение этой энергии по разным направлениям оказывается неодинаковым. Согласно закону Ламберта, количество энергии , излучаемой теплом в направлении, составляющей с нормалью к поверхности угол , определяется по уравнению

. (51)

Опыт показывает, что закон Ламберта строго справедлив только для абсолютно черного тела. У серых тел этот закон подтверждается лишь в пределах .

Применение законов лучистого теплообмена и представление об эффективной плотности теплового потока позволяют найти расчетные зависимости для результирующего теплового потока между твердыми телами, разделенными прозрачной средой (D =1).

Тепловой поток между двумя параллельными пластинами 1 и 2 неограниченных размеров ( ), Вт:

(52)

где − приведенная степень черноты системы; площадь пластины

Тепловой поток между двумя телами, одно из которых находится в полости (оболочке) другого тела; поверхность внутреннего тела F₁ – выпуклая, внешнего F₂ – вогнутая; температура внутреннего тела Т₁, а внешнего Т₂, причем Т₁>Т₂:

(53)

где ; − угловой коэффициент излучения, характеризующий часть излучения внешней поверхности, попадающей на внутреннюю. Если то

. (54)

Пример 8. Определить потери тепла излучением с 1 м паропровода, если его наружный диаметр м, степень черноты поверхности , температура стенки , температура окружающих тел .

Решение. При излучении в неограниченное пространство, когда

Лучистый теплообмен в различных излучающих системах может быть уменьшен за счет применения экранов. Если между двумя плоскостями параллельными поверхностями установлен экран в виде тонкой пластины, (газовый слой прозрачен, D=1), то с первой пластины на вторую (при Т₁>Т₂) может попасть лишь часть потока тепла, поглощаемая экраном (прозрачность экрана равна нулю, D_э=0). Расчетным уравнением в этом случае является зависимость (52), в которой приведенная степень черноты для общего случая n – экранов

23

, (55)

где - степень черноты i–го экрана.

Пример 9. Решить задачу, рассмотренную в предыдущем примере, при условии, что паропровод окружен экраном: и .

Решение. Температуру экрана определяем из уравнения баланса теплового потока:

Приведенная степень черноты для системы паропровод – экран:

.

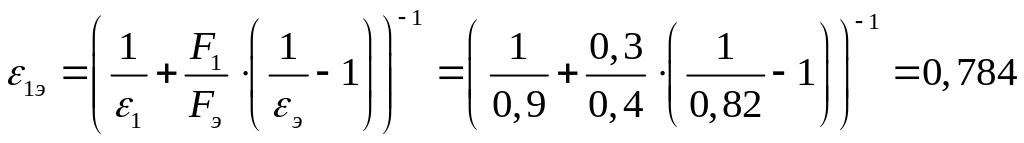Из уравнения баланса находим :

.

Особенностью излучения газовых объемов является то, что количество поглощаемой трех – или многоатомным газом (углекислым газом СО₂, водяным паром Н₂О и др.), энергии зависит от числа микрочастиц в объеме, которое пропорционально толщине газового слоя, характеризуемой длиной пути луча l, парциальному давлению газа р и его температуре Т. В соответствие с этим, степень черноты газового слоя зависит от температуры, давления и толщины этого слоя, т.е. . Плотность излучения с поверхности газового слоя на окружающие его стенки

, (56)

где − эффективная степень черноты оболочки; − поглощательная способность газа при температуре стенки. Средняя длина пути луча приближенно определяется как , где − объем газа; − поверхность оболочки.

Сложный (комбинированный) теплообмен. В реальных условиях эксплуатации различных технических систем теплота может одновременно передаваться теплопроводностью, конвекцией и излучением. Такой теплообмен называют сложным.

Если газообразная среда прозрачна для тепловых лучей (D=1), то расчет теплообмена осуществляют, используя принцип аддитивности (суммирования) тепловых потоков за счет отдельных способов (механизмов) теплообмена. В наиболее общем случае радиационно– конвективной теплоотдачи величина теплового потока от стенки к омывающему ее газу и к окружающим телам путем соответственно конвективной теплоотдачи Q_к и теплового излучения Q_р через прозрачный газ, Вт

, (57)

где − температура соответственно стенки и газа за пределами пограничного слоя; − площадь поверхности теплообмена стенки; − приведенная степень черноты системы; − температура окружающих тел (оболочки).

Если газовый объем ограничен стенками и его толщина соизмерима с толщиной пограничных слоев, то теплообмен рассматривают как радиационно–кондуктивный и в расчете учитывают метод эквивалентной теплопроводности, рассмотренный выше.

Пример 10. Определить радиационно–конвективный коэффициент теплоотдачи от панельного комнатного радиатора высотой Н = 0,4 м, обогреваемого водой температурой 90 ⁰С. Температура воздуха и стен в помещении t_ж = 18 ⁰С. Степень черноты поверхности радиатора .

24

Решение. В соответствие с формулами (53) и (57), при условии равенства температур и имеем

где 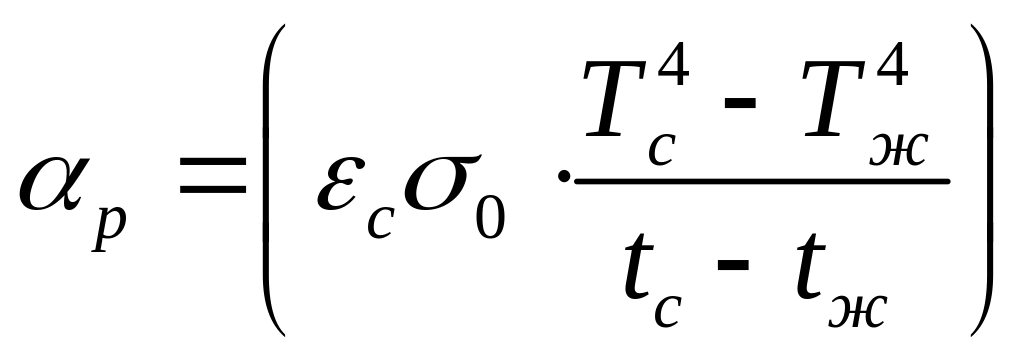− радиационный коэффициент теплоотдачи.

В данном случае конвективная теплоотдача обусловлена свободным (термогравитационным) движением воздуха вдоль вертикальной стенки радиатора. Определяющая температура .

По таблице А2 находим: ; .

Критерий Рэлея:

.

По уравнению (43):

.

Конвективный коэффициент теплоотдачи .

Радиационный коэффициент теплоотдачи

Суммарный радиационно–конвективный коэффициент теплоотдачи

Следовательно, в нагревательных элементах значительная часть теплоотдачи осуществляется тепловым излучением.