1 Теплопроводность

Температурное поле и закон Фурье. Теплопроводность определяется тепловым (хаотическим) движением микрочастиц тела. В теории теплопроводности вещество рассматривается как сплошная среда, перенос теплоты в которой (при отсутствии конвекции и излучения) обусловлен наличием разности температур.

Совокупность значений температур всех макроскопических точек тела в данный момент времени  называется температурным полем.

, (1)

где - координаты любой точки тела.

Если температура тела не изменяется с течением времени, то температурное поле стационарное, т.е.

(2)

Мысленно соединяя все точки тела с одинаковой температурой, получим поверхность, называемая изотермической. Изотермические поверхности не пересекаются и при пересечении их плоскостью дают на ней семейство изотерм (рис.1).

5

Рис. 1 – Семейство изотерм в плоском сечении тела

Интенсивность изменения температуры в произвольном направлении s через элементарную площадку dF характеризуются производной ( ), принимающей наибольшее значение в направлении нормали к изотермической поверхности:

. (3)

Температурный градиент ( ) направлен в сторону возрастания температуры по нормали п. Количество теплоты, прошедшее в единицу времени через элемент изотермической поверхности, называется плотностью теплового потока . С учетом направления потока тепла, согласно закону Фурье, Вт/м²

(4)

Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком, Вт

. (5)

Множитель , называемый коэффициентом теплопроводности ( ), является теплофизическим свойством вещества. Теплопроводность газов ( ) растет с повышением температуры и давления, а жидкости ( ) – обычно уменьшается с ростом температуры. Наилучшими проводниками тепла являются металлы ( ); теплопроводность металлов убывает с ростом температуры и повышением количества легирующих элементов.

Твердые материалы, у которых , относят к теплоизоляторам. Большинство теплоизоляционных и строительных материалов имеют пористое строение, что объясняет их низкую теплопроводность.

Описание теплопроводности. Решение задач теплопроводности связано с определением поля температур (2) и тепловых потоков (5). Для этого, используя первый закон термодинамики и зависимость (4) получают дифференциальное уравнение теплопроводности:

(6)

При выводе (6) предполагалось, что тело однородно и изоэнтропно, физические параметры (теплопроводность , теплоемкость с и плотность ) постоянны, внутренние источники теплоты мощностью , Вт/м³ равномерно распределены в теле. Величину называют коэффициентом температуропроводности материала тела (м²/с).

6

Для однозначного решения уравнения (6) и определения постоянных интегрирования его необходимо дополнить условиями однозначности (краевыми условиями) определяющими параметрами конкретной задачи. Выделяют следующие краевые условия: геометрические – характеризующие форму и размеры тела; теплофизические – характеризующие свойства тела ( ); временные – характеризующие распределения температуры тела в начальный момент времени, например, при =0; граничные – характеризующие взаимодействие тела с окружающей средой.

Граничные условия бывают четырех видов (родов): 1 рода (задается распределением температуры на поверхности тела в функции времени); 2 рода (задается плотность теплового потока для поверхности тела в функции времени); 3 рода (задается температура окружающей среды (жидкости или газа) и уравнение теплоотдачи (см. (17)) между поверхностью тела и средой); 4 рода (условия совместимости, задаваемые в виде равенства температур и тепловых потоков соприкасающихся тел).

Теплопроводность через плоскую стенку при граничных условиях 1 рода. Рассмотрим однородную плоскую стенку толщиной  на наружных поверхностях которой поддерживается постоянные температуры и (рис. 2). Коэффициент теплопроводности материала стенки (в расчетах обычно принимается среднее значение λ). При стационарном режиме ( ) и отсутствии внутренних источников тепла ( ) дифференциальное уравнение запишется в виде

(7)

т.к. при заданных условиях температура меняется только в направлении, перпендикулярном плоскости стенки ( ).

Граничные условия имеют следующий вид

(8)

Из решения (7), (8) следует линейное распределение температуры по толщине плоской стенки

(9)

При этом плотность теплового потока

(10)

где - термическое сопротивление теплопроводности через плоскую стенку ( ).

Очевидно, что при стационарном теплообмене, Вт

(11)

Если стенка состоит из п однородных слоев с коэффициентами теплопроводности и толщинами , то при стационарном режиме тепловой поток через любой слой одинаков, т.е.

. (12)

Для плоской стенки будет одинакова и плотность потока , т.к. .

На основании (11) и (12) получим

(13)

7

где - температурный напор (разность температур) для рассматриваемых слоев;

- термическое сопротивление теплопроводности i – го слоя.

При расчете температурного поля формулу (13) можно использовать либо для всех слоев, либо для определенной группы рассматриваемых слоев.

Рис. 2 – Теплопроводность через однородную плоскую стенку

Пример 1. Определить плотность теплового потока , проходящего через трехслойную плоскую стенку, если толщины слоев а соответствующее значение коэффициентов теплопроводности Температуры на поверхностях стенки: Найти температуры стенок на границах соприкосновения слоев

Решение. Термические сопротивления слоев

Суммарное сопротивление стенки

Плотность теплового потока

Температуры на границе слоев

Теплопроводность через цилиндрическую стенку при граничных условиях первого рода. В отличии от стационарной теплопроводности через плоскую стенку, когда площадь поверхности теплообмена постоянна (F = const), в данном случае площадь теплообмена увеличивается при переходе от внутренней поверхности ( ) к наружной ( ). Из решения краевой задачи следует ,что распределение температуры по толщине цилиндрической стенки логарифмическое, т.е.

, (14)

8

где - текущая координата цилиндрической стенки. При использовании граничных условий ( ) определяем постоянную интегрирования С и получаем формулу для расчета потока через цилиндрическую стенку, Вт:

(15)

где - линейное термическое сопротивление цилиндрического слоя, .

Для многослойной цилиндрической стенки, с учетом условия стационарности (13), получим

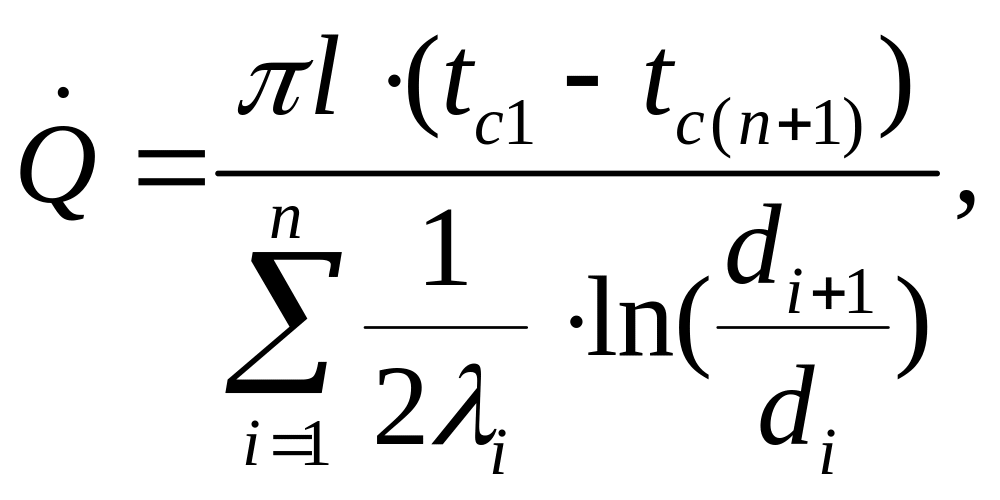(16)

При использовании достаточно тонких цилиндрических труб (когда отношение наружного диаметра к внутреннему меньше двух: профиль температуры (14) незначительно отличается от линейного и поэтому, с погрешностью менее 3% расчет можно проводить через условную плоскую стенку толщиной с площадью теплообмена

Теплопроводность через стенку с граничными условиями третьего рода (теплопередача). Теплообмен от одной подвижной среды (жидкости или газа) к другой через разделяющую их твердую стенку любой формы называют теплопередачей. Примером теплопередачи служит перенос тепла от горячих продуктов сгорания (топочных газов) к воде через стенки труб парогенератора, включающий конвективную теплоотдачу от газов к внешней стенке, теплопроводность в стенке и конвективную теплоотдачу от внутренней поверхности стенке к воде. Особенности протекания процесса на границах стенки при теплопередаче характеризуются граничными условиями 3 рода, которые задаются температурами жидкости (газа) с обеих сторон стенки, а также соответствующими значениями коэффициентов теплоотдачи  в уравнении Ньютона – Рихмана, Вт:

(17)

Рассмотрим стационарную теплопередачу через плоскую стенку толщиной . Заданы коэффициент теплопроводности стенки, температуры сред, омывающих стенку, и ( ), коэффициенты теплоотдачи и . Необходимо найти тепловой поток (для плоской стенки F= сonst) и температуры на поверхности стенки . Для трех слоев теплообмена имеем:

(18)

C учетом условия стационарного теплообмена (12), получим

, (19)

где к – коэффициент теплопередачи ( ); - суммарное термическое сопротивление теплопередачи:

9

Неизвестные температуры t_c1 и t_c2 определяют по формулам (18) после определения плотности потока тепла . Для многослойной плоской стенки термическое сопротивление теплопроводности находится как

Для цилиндрической стенки после аналогичных преобразований получим уравнение теплопередачи в виде

(20)

где - линейный коэффициент теплопередачи, .

Пример 2. Определить потерю тепла с 1 м трубопровода диаметром , покрытого слоем изоляции толщиной Коэффициент теплопроводности трубы , а изоляции - Температура воды в трубопроводе , а окружающего воздуха . Коэффициенты теплоотдачи: Вычислить температуру на внешней поверхности изоляции.

Решение: Линейный коэффициент теплопередачи

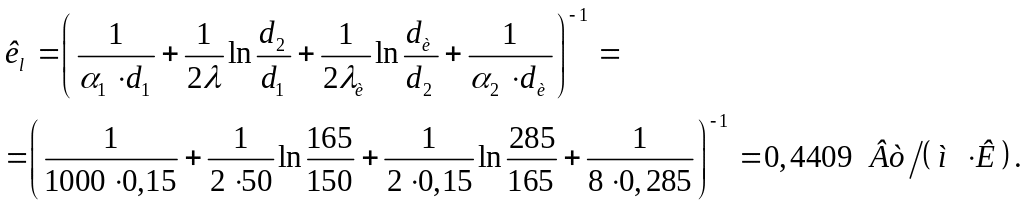(21)

Линейная плотность теплового потока

.

Температура на поверхности изоляции

Особенности тепловой изоляции тонких труб. Тепловой изоляцией называют покрытие из теплоизоляционного материала, которое способствует снижению потерь тепла в окружающую среду. Если цилиндрическая стенка покрыта изоляцией, то, согласно формуле (20) в примере, увеличение толщины изоляции, а значит и диаметра , приводит к росту сопротивления теплопроводности и одновременно – к снижению сопротивления внешней теплоотдачи ( ). Анализ ситуации показывает, что условием выбора тепловой изоляции является неравенство:

Пример 3. Для изоляции трубы диаметром предлагалось использовать пенобетон с теплопроводностью Задан коэффициент теплоотдачи

10

Решение. Тепловая изоляция должна удовлетворять условию Следовательно, пенобетон не может быть использован, т.к. покрытие этим материалом приведет к обратному эффекту.

Интенсификация теплопередачи. При неизменной разности температур между теплоносителями плотность теплового потока зависит от коэффициента теплопроводности k. Т.к. теплопередача представляет собой комплексное и сложное явление, рассмотрение путей ее интенсификации связано с анализом составляющих процесса. В случае плоской металлической стенки, когда ,

Отсюда видно, что коэффициент теплопередачи всегда меньше самого малого из коэффициентов теплоотдачи. Для повышения коэффициента теплопередачи нужно увеличивать наименьший коэффициент теплоотдачи или . Если , то следует увеличивать и , и . Теплообмен можно интенсифицировать путем оребрения стенки со стороны меньшей теплоотдачи. Тепловой поток через оребренную плоскую стенку (при условии, что )

, (22)

где − коэффициент теплоотдачи оребренной стенки; -эффективный коэффициент теплоотдачи от оребренной поверхности. При использовании достаточно тонких ребер , где − коэффициент теплоотдачи оребренной стенки; − коэффициент эффективности ребра ; − степень оребрения; − площадь поверхности оребренной стенки.

Как следует из (22), оребрение поверхности позволяет выравнивать термические сопротивления теплоотдачи и тем самым интенсифицировать теплопередачу.