Т. Е. Оо' всегда больше ос. Точка подвеса о маятника и центр качаний о' обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка о подвеса

станет новым центром качаний, и период колебаний физического маятника не изменится.

3. Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятника

                                                                     (142.8)

где l — длина маятника.

Так как математический маятник можно представить как частный случай физичес­кого маятника, предположив, что вся его масса сосредоточена в одной точке — центре масс, то, подставив выражение (142.8) в формулу (1417), получим выражение для периода малых колебаний математического маятника

                                                    (142.9)

Сравнивая формулы (142.7) и (142.9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

Простая колебательная система при наличии трения.

Рассмотрим простую механическую колебательную систему (рис. 1), состоящую из массы т, укрепленной на пружине имеющей упругость s. Масса находится в вязкой среде, создающей сопротивление трения r. Если конец пружины оттянут из положения равновесия на расстояние х, то пружина стремится сократиться с некоторой силой. Очевидно, что эта сила тем больше, чем на большее расстояние оттянута пружина и чем больше ее упругость. Отсюда возвращающая сила пружины F_s, стремящаяся вернуть оттянутый ее конец в положение равновесия, равна произведению xs, где х — расстояние, на которое оттянут конец пружины, a s — коэффициент упругости пружины.

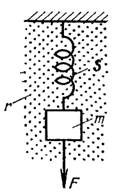
Рис. 1. Простая механическая колебательная система

В свою очередь s определяется как s=F _s / x.

Отсюда единицей упругости называется упругость такой пружины, которая при растяжении на единицу длины (1 м) стремится сократиться с силой, равной также единице (1 Н).

Свойства пружины можно характеризовать и величиной, обратной коэффициенту упругости. Эта величина называется коэффициентом гибкости и обозначается буквой с: c=1/s и соответственно c=x/F_s.

При перемещении тела возникают силы трения, тормозящие движение тела. При движении тела в вязкой среде значение силы трения F_r пропорционально скорости тела х и коэффициенту r, характеризующему среду, в которой возникает трение, и называемому обычно сопротивлением трения. Следует заметить, что сопротивление трения может возникать не только при движении тела в вязкой среде, но и в результате внутреннего трения, например, трения частиц в толще материала пружины при ее растяжении или сжатии.

Сопротивление трения — одна из составляющих активного механического сопротивления. Характерной особенностью реальной механической системы (обладающей активным механическим сопротивлением) является то, что в ней всегда имеет место необратимый переход механической энергии в тепловую.

Затухающие колебания.

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.

(7.17)

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ 

или

(7.18)

Перепишем это уравнение в следующем виде:

и обозначим:

где   представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

(7.19)

Будем искать решение уравнения (7.19) в виде где U - некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим 

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение   тогда С вещественным ω решением этого уравнения, как мы знаем, является функция 

Таким образом, в случае малого сопротивления среды   , решением уравнения (7.19) будет функция

(7.20)

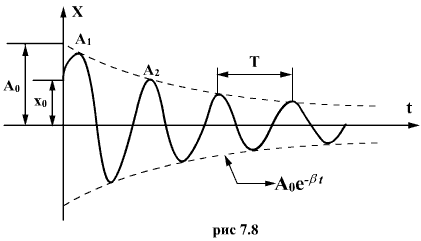
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину   называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину   обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда

откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

Дифференциальное уравнение и его решение.

Дифференциальное уравнение свободных затухающих колебаний линейной системы определяется как   (1)  где s – колеблющаяся величина, которая описывает тот или иной физический процесс, δ = const — коэффициент затухания, ω₀ - циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.  Решение уравнения (1) запишем в виде   (2)  где u=u(t). После взятия первой и второй производных (2) и подстановки их в выражение (1) найдем   (3)  Решение уравнения (3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай положителньного коэффициента:   (4)  (если (ω₀² - σ²)>0, то такое обозначение мы вправе сделать). Тогда получим выражение   , у которого решение будет функция   . Значит, решение уравнения (1) в случае малых затуханий (ω₀² >> σ² )   (5)  где   (6) 

Характеристики затухающих колебаний: коэффициент затухания, логарифмический декремент затухания, добротность, время релаксации.