Практика бағдарламасы

№	Тақырыптар	Уақыты
1.	Циклдық және тармақталған алгоритмдер	27.05.2013
2.	Кірістірілген циклдер	28.05.2013
3.	Матрицалық есептерде кірістірілген циклдар	29.05.2013
4.	Көп өлшемді массивтер	30.05.2013
5.	Символдық типті массивтер. Жол және оған қолданылатын өрнектер.	31.06.2013
6.	Мәтiндiк файлдар. Мәтiндiк файлға жазу.Файлдың элементтерiнiң өңдеуi. бастапқы файлды өзгерту. Бiрнеше файлдармен жұмыс жасау. Оқу, жою және мәтiндiк файлға мәлiметi енгізу.	1.06.2013
7.	Сызықтық емес теңдеулерді шешудің кесіндіні қақ бөлу әдісі	3.06.2013
8.	Сызықтық емес теңдеулерді шешудің кесіндіні жанамалар (Ньютон) әдісі	4.06.2013
9.	Анықталған интегралды жуықтап есептеудің тіктөртбұрыштар әдісі	5.06.2013
10.	Анықталған интегралды жуықтап есептеудің трапециялар әдісі	6.06.2013
11.	Анықталған интегралды жуықтап есептеудің Симпсон әдісі	7.06.2013
12.	Практиканы қорғау	8.06.2013

Функция және оның графигі

Функция – басқа мәліметтер алу үшін анықталған мәліметтерге қолданылатын компьютердің іс-әрекеті. Функцияның ерекшелігі – оның орындалуы барысында бір ғана нәтиже шығады, ал енгізілген параметрлері бірнешеу болуы мүмкін. Нәтиже функция атауымен белгіленіп, негізгі бағдарламаға беріледі.

Функцияның анықталуы:

int simple_function ()

{

return 0;

}

Функция екі жағдайда қолданылады:

1. Егер функция денесіндегі опетаторлар, программада көп кездескенде. Онда, оларға бөлек функция жариялаймыз. Осы жағдайда, программа коды қысқарады.

2. Егер программада, бірнеше операторлар қандай да бір нақты тапсырманы орындаған жағдайда. Осы жағдайда, программа көлемі қысқармауы мүмкін , бірақ программа нақтырақ болады.

#include<iostream.h>

#include<math.h>

#include<fstream.h>

void main()

{ofstream write_file("mk.dat");

int a,b,n,h;

cin >> a >> b >> n;

h=(b-a)/n;

for(double x=a;x<=b;x+=h)

{

cout << x << " " <<(cos(x)*sin(x))/(cos(x)-2*cos(x)) << endl;

write_file<< x << " " << (cos(x)*sin(x))/(cos(x)-2*cos(x)) << endl;}

}

}

2) #include<iostream.h>

#include<math.h>

#include<fstream.h>

void main()

{ofstream write_file("mk.dat");

int a,b,n,h;

cin >> a >> b >> n;

h=(b-a)/n;

for(double x=a;x<=b;x+=h)

{

cout << x << " " <<(pow(x,5)+pow(x,3)-pow(x,2))/(pow(x,6))<< endl;

write_file<< x << " " << (pow(x,5) +pow(x,3)-pow(x,2))/(pow(x,6))<< endl;} }

3)

#include<iostream.h>

#include<math.h>

#include<fstream.h>

void main()

{ofstream write_file("mk.dat");

int a,b,n,h;

cin >> a >> b >> n;

h=(b-a)/n;

for(double x=a;x<=b;x+=h)

{

cout << x << " " <<sin(2*x)+cos(x*5)-5<< endl;

write_file<< x << " " << sin(2*x)+cos(x*5)-5<< endl;}}

Тік төртбұрыш әдісі.

интегралды жуықтап былайша есептейміз:

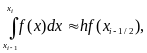(1.1)

мұндағы

Бұл формуланың геометриялық мағынасы мынандай:

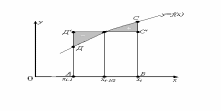2-сурет

АВСД қисық сызықты трапецияның ауданы биіктігі АВД^/C^/ тік төртбұрышының ауданымен алмастырылады (2-сурет).

Сондықтан бұл формуланы тік төртбұрыш әдісі дейді.

(1.1) формуласының дәлдігі

. (1.2)

Тейлор формуласы арқылы оңай табылады.

Шынында да 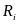ді былайша жазып

= (1.3)

және +

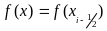десек, онда (1.3) формуласынан

(1.4)

формуласын аламыз.

Егер М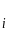 = деп R -ді жоғарыдан бағаласақ ,онда

Яғни (1.5)

болғандықтан, h 0 ұмтылғандағы дәлдік 0(h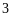 ) болады.

Енді (1.1) теңдіктің i-дің 1 ден N ге дейінгі қосындысын қарастырсақ

(1.6)

болады. Сондықтан .

Осыдан

.

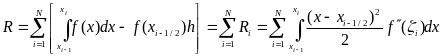Егер десек, онда

, (1.7)

яғни тік төртбұрыш әдісінің 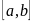кесіндісіндегі дәлдігі-0(h ).

С++ тілінде есепті жүзеге асыру программасы:

#include <iostream.h>

#include <math.h>

double f(double x)

{

return x;

}

void main()

{ double a,b,s,x[100],J1,J2,h,h1;

float e,s1,s2;

int n;

cin >> a >>b >>n;

h=(b-a)/n;

h1=(b-a)/(2*n);

s1=0;s2=0;

for(double i=a+h; i<=b; i+=h)

{s1+=f(i);}

J1=s1*h;

cout<<"J1="<<J1<<endl;

for( i=a+h1; i<=b; i+=h1)

{s2+=f(i);}

J2=s2*h1;

cout<<"J2="<<J2<<endl;

e=fabs(J2-J1);

cout<<"e=fabs(I2-I1)="<<e<<endl;}

1) a=1;b=5;n=10

2) a=1;b=5;n=100

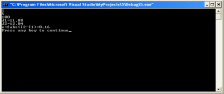
3)a=1;b=5;n=1000

Трапеция әдісі.

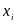функциясын нүктелері арқылы тұрғызылған

бір дәрежелі Лагранж көпмүшесімен алмастырсақ, онда

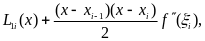(1.8)

мұндағы

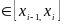
(1.8) формуласын аралығында интегралдау арқылы

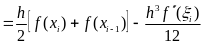(1.9)

теңдігін аламыз. Осыдан

. Бұл формула трапеция әдісі деп аталады,себебі

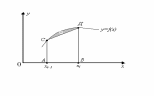
3-сурет

сызықтарымен қоршалған қисық сызықты трапецияның ауданы 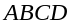трапециясының ауданымен алмастырылады (3сурет).

(1.9) формуладан бұл әдістің жіберетін қатесі

(2)

екенін көреміз. Ал жоғарыдан бағаласақ

,

Енді интегралды былай есептесек:

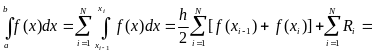
(2.1)

Онда

(2.2)

трапеция әдісінің жалпы формуласы шығады.

Ал жіберілетін қате

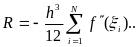(2.3)

Жоғарыдан бағаласақ

, (2.4)

.

Сонымен, трапеция әдісінің кесіндісіндегі дәлдігі екенін көреміз.

#include <iostream.h>

#include <math.h>

double f(double x)

{ double s=x;

return s;

}

void main()

{double a,b,s,s1,J1,J2,x[100];

float h,h1,c,e;

int n;

cin >>a >>b >>n;

s=0;

s1=0;

h=(b-a)/n;

h1=(b-a)/(2*n);

c=(f(b)-f(a))/2;

for( double i=a+h; i<b; i+=h)

{

s+=f(i);}

J1=(c+s)*h;

cout<<"J1="<<J1<<endl;

for(double j=a+h/2; j<b; j+=h/2)

{

s1+=f(j);}

J2=(c+s1)*h/2;

cout<<"J2="<<J2<<endl;

e=fabs(J2-J1);

cout<<"e=fabs(J2-J1)="<<e<<endl;}

1) a=1;b=5;n=10

2) a=1;b=5;n=100

3) a=1;b=5;n=1000

Парабола әдісі. (Симпсон формуласы).

интегралды жуықтап есептеу үшін функциясын нүктелері арқылы тұрғызылған Лагранж көп мүшесімен алмастырамыз. Яғни

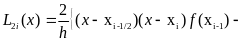
. (1)

Осыдан

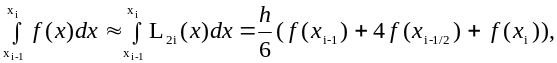
Сонымен мына формуланы –

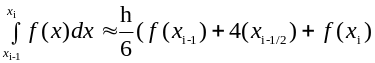(1.1)

Симпсон немесе парабола формуласы деп атайды.

Бұл формуланың парабола формуласы деп атайтын себебі

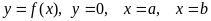сызықтарымен шектелген қисық сызықты трапецияның ауданы нүктелері арқылы өтетін парабола және түзулерімен шектелген трапецияның ауданымен алмастырылады (4-сурет).

Симпсон формуласы кесіндісінде былайша жазылады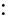

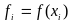
Бөлшекті индекстерден құтылу үшін

десек,онда Симпсон формуласын былайша жазамыз:

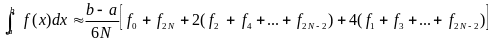. (1.3)

4-сурет

О х у x_i-1 x_i-1/2 x_i y=f(x) y=L₂(x) + -

Симпсон формуласының жіберетін қатесін қарастырардың алдында, оның үш дәрежелі көпмүше үшін дәл екенін көрсетейік. Шынында да

болса, онда

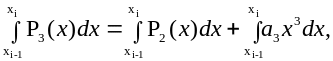
Осыдан

Екіншіден

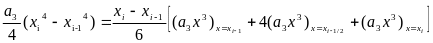
екенін ескерсек

формуласын аламыз.

Сонымен Симпсон формуласының үшінші дәрежеге дейінгі кез келген көпмүшелер үшін дәл екенін көрдік.

Енді Симпсон формуласының қатесін қарастыру үшін мына шарттарды қанағаттандыратын

интерполяциялық Эрмит көпмүшелігін пайдаланамыз .

Симпсон формуласы кез келген үш дәрежелі көпмүшеліктер үшін дәл болғандықтан

(1.4)

Енді

десек,онда

мұндағы (1.5)

-Эрмит көпмүшесінің жіберетін қатесі.

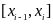кесіндісінде көпмүшесі өзінің таңбасын өзгертпейтін болғандықтан

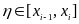
Сондықтан Симпсон формуласының жіберетін қатесi

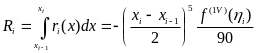. (1.6)

Hемесе

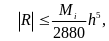(1.7)

Симпсон формуласының кесіндісінде жіберетін қатесі

Болғандықтан (1.8)

Яғни Симпсон әдісінің кесіндісіндегі дәлдігі .

С++ тілінде есепті жүзеге асыру программасы:

#include <iostream.h>

#include <math.h>

double f(double x)

{ return x;

}void main()

{ double a,b,s,s1,s2,J1,J2,e1,e2,e3;

float h,h1,h2,k;

int n;

double c,c1,c2;

cin >> a>> b >> n;

s=0;c=0;c1=0;s1=0;

h=(b-a)/(2*n);

h1=(b-a)/(4*n);

k=f(a)+f(b);

for(double i=a+h; i<b; i+=2*h)

{c+=f(i);}

for (i=a+2*h; i<b; i+=2*h)

{ s+=f(i);}

J1=(k+4*c+6*s)*h/2;

cout<<"J1="<<J1<<endl;

for(i=a+h1; i<b; i+=2*h1)

{c1+=f(i);}

for (i=a+2*h1; i<b; i+=2*h1)

{ s1+=f(i);}

J2=(k+2*c1+3*s1)*h1/2;

cout<<"J2="<<J2<<endl;

e1=fabs(J2-J1);

cout<<"e1=fabs(J2-J1)="<<e1<<endl;

}

1)a=1;b=5n=10

2)a=1;b=5;n=100

3)a=1;b=5;n=1000