3.2 Порядок виконання експериментальної частини.

Експеримент реалізується в порядку номерів дослідів графи 6 табл. 1. Відповідно до умов дослідів вибираються деталі необхідної маси, включається секундомір і виконується установка деталі в лещата. Точність установки контролюється за допомогою індикатора, остаточне закріплення деталі і зупинка секундоміра здійснюється тільки тоді, коли точність установки не перевищує зазначеної в умовах досліду погрішності. Час установки записується в графу 7 табл. 1.

3.3 Обробка результатів експериментів

Обробка результатів експериментів виконується в наступній послідовності:

1 Визначаємо lg t_shtm.

2 Обчислюємо середні значення lg t_shtcp:

3 Обчислюємо дисперсії відхилень lg t_shtm від lg t_shtср:

4 Оцінюємо однорідність дисперсій за критерієм Кохрена:

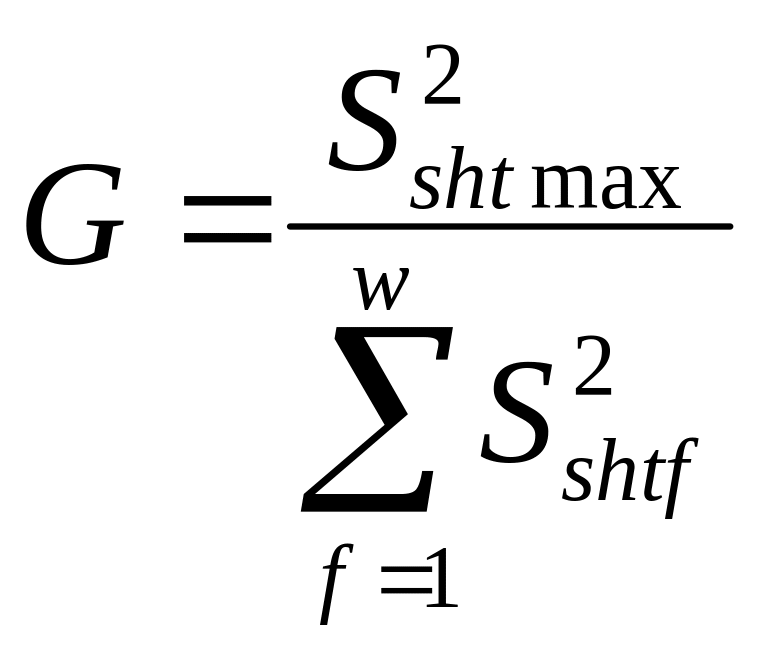
Якщо G = G_kp, обумовленого по таблиці (додаток Ж) для рівня значимості  = 0,05 і числа ступенів свободи N ², то дисперсії можна вважати однорідними.

Це дозволяє обчислити дисперсію відтворюваності дослідів шляхом усереднення дисперсій:

При G > G_kp дисперсії визнаються неоднорідними. У цьому випадку необхідно зробити додаткові досліди в кожній точці плану, а також перевірити наявність помилок експерименту, після чого знову обчислити G – критерій.

5 Визначаємо коефіцієнти моделі. Коефіцієнти b₀, b₁, b₂ обчислюються за формулою:

Примітка: 1. i = 0, 1, 2.

Таблиця 1 – Обробка експериментальних даних

Точка плану (f)	x1 (м)		x2 (Е)		№ досліду	tshtm	lg tshtm	lg tshtcpf		lg* tshtf	y2shtf
	Код	кг	код	мм
1	2	3	4	5	6	7	8	9	10	11	12
1
2
3
4
5

2. x₀ = +1 у всіх точках плану.

У зв'язку з цим

6. Оцінюємо значимість коефіцієнтів.

Значимість коефіцієнтів, тобто їхня відмінність від нуля визначається порівнянням коефіцієнта b_i з його довірчим інтервалом Δb_i.

Коефіцієнт статистично значимий у випадку b_i > Δb_i. У противному випадку b_i = 0.

Довірчий інтервал

,

де t – критерій Стьюдента (див. додаток Г);

- середньоквадратичне відхилення коефіцієнта b_i

Значення t – критерію визначається для числа ступенів свободи К = v-1 = 24 при довірчій імовірності Р = 0,95 (t = 2,06).

6. Оцінюємо адекватність моделі.

Розрахункові значення lg^* t_shtf визначаються з урахуванням значимості коефіцієнтів по моделі:

,

де x₁ і x₂ – кодовані значення перемінних (+1, 0, -1);

b₀, b₁, b₂ – коефіцієнти моделі, обчислені відповідно до пункту 5.

Розрахуємо квадрат помилки

Дисперсія адекватності

,

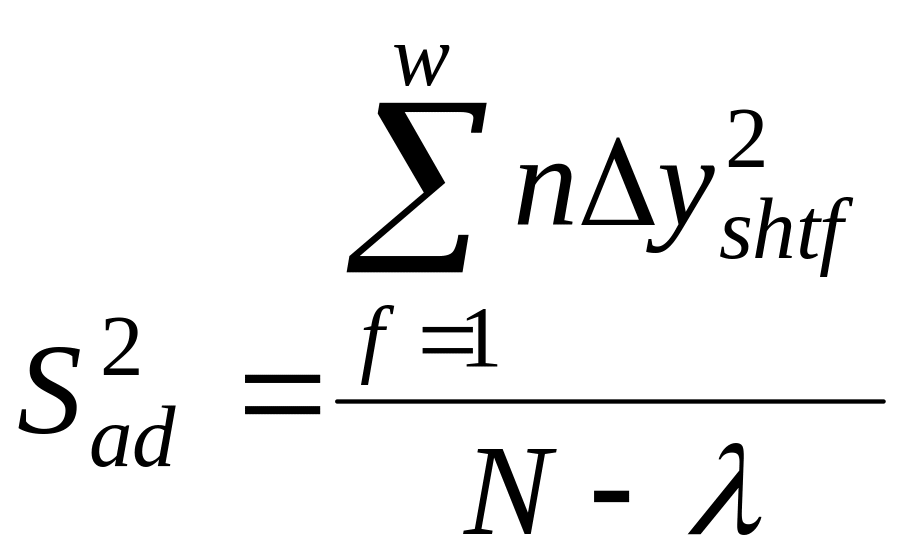де λ – кількість коефіцієнтів моделі, λ = 3.

Як критерій адекватності використовується F – критерій Фішера:

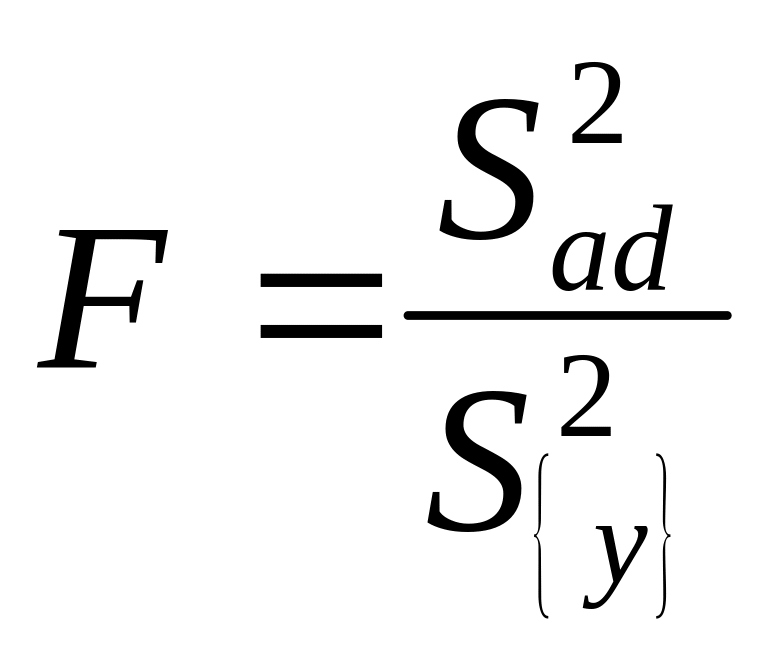
Якщо F < F_табл (додаток В), обумовленого для числа ступенів свободи дисперсії адекватності f_ad = 2 і числа ступенів свободи дисперсії відтворюваності f_vosp = 4 при рівні значимості α = 0,05 (Р_табл = 6,94), то отримана модель може бути визнана адекватною з довірчою імовірністю Р = 0,95.

При F > F_табл модель непридатна для практичного використання. У цьому випадку необхідно збільшити кількість повторних дослідів або застосувати планування другого порядку.

8 Перетворення кодованих перемінних у натуральні.

Для одержання залежності виду (1) з рівняння (6) необхідно зробити наступні заміни:

4 Зміст звіту

1. Титульний аркуш.

2. Схема виміру погрішності установки заготовки.

3. Робоча матриця плану.

4. Математична обробка результатів.

5. Висновки за результатами досліджень (оцінка однорідності дисперсії дослідів, оцінка адекватності моделі, пропозиції по удосконалюванню моделі).