1.2. Исследуемые закономерности

В состав экспериментальной установки входит нагретая до высокой (T ~ 1000 K) температуры тонкая металлическая пластина с площадью поверхностиS= . По существующей классификации пластина относится к числу серых тел. Поглощательная способность пластины имеет значение. В процессе эксперимента производится измерение мощности теплового излученияP_ТИ, создаваемого пластиной, и ее температурыT.

Для измерения температуры пластины в работе используется неконтактный термометр (оптический пирометр). Через окуляр зрительной трубы пирометра наблюдатель видит (рис. 1.1, а) светящуюся нить (основная часть пирометра) на фоне светящейся поверхности исследуемого тела. Увеличение силы тока в нити пирометра приводит к возрастанию ее температуры и яркости свечения. При определенной яркости нить становится невидимой (рис. 1.1,б) на фоне светящейся поверхности. Если бы оба тела (нить и пластина) являлись бы абсолютно черными телами, то одинаковость яркости их свечения свидетельствовало бы о равенстве температур. В экспериментальной же установке нить пирометра является эквивалентом абсолютно черного тела, а нагреваемая пластина относится к классу серых тел.

Рис. 1.1.Видимое изображение нагретой нити2на фоне светящейся поверхности исследуемого тела1при разнойа) и одинаковойб) светимости тел

Яркость определяется как суммарная плотность потока энергии, переносимая электромагнитными волнами разных частот, в пределах телесного единичного угла:

. (1.8)

Одинаковое свечение нити с температурой и пластины с температурой, зафиксированное наблюдателем с помощью пирометра, свидетельствует о выполнении равенства:

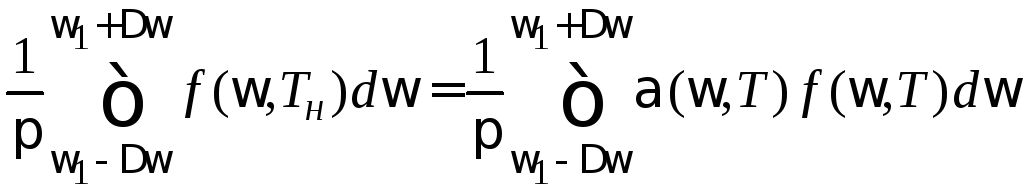. (1.9)

Здесь использованы следующие обозначения: – центральная частота светофильтра, входящего в состав пирометра;  – полоса частот пропускания светофильтра ( _); – поглощательная способность поверхности пластины на частоте_. Для красного светофильтра пирометрадлина волны в вакууме составляет_ = 665 нм, для желтого₂ = 600 нм.Математические преобразования равенства (1.9), выполненные с учетом малости отношения /_  1, приводят к алгебраическому выражению, связывающему искомую температуру пластины Т с измеренным значением температуры нити:

. (1.10)

Основу методики измерения мощности излучения пластины составляет условие теплового равновесия. В состоянии термодинамического равновесия выполняется баланс между приобретаемой и теряемой в единицу времени энергии. Условие равновесия, учитывающее основные механизмы обмена энергией между пластиной и окружающими телами, формулируется в виде равенства

, (1.11)

в котором Р– мощность Джоуля–Ленца, выделяющаяся в пластине при протекании электрического тока;– поглощаемая пластиной мощность теплового излучения, генерируемое окружающими телами;– мощность теплопроводности, которая передается от пластины к другим узлам экспериментальной установки за счет механизма теплопроводности, например, соединительных проводников. Если площадь поверхности пластиныSвелика по сравнению с площадью поперечного сеченияS₁проводников (S₁<<S) и температура пластиныTпревышает температуруT₀окружающей среды в несколько раз, то, а мощность излучения пластинысущественно превышает мощность радиационного поглощенияи мощность теплопроводности. В этом случае мощность излучениясовпадает с мощностью Джоуля–Ленца. Отсюда в соответствии с законом Стефана-Больцмана (1.6) получаем

(1.12)

На основании теоретического прогноза (1.12) исследуемая зависимость мощности излучения от температуры пластины P(T) должна соответствовать степенной функции

, (1.13)

в которой n – показатель степени; — коэффициент пропорциональности, содержащий площадьSповерхности пластины, поглощательную способность₁и постоянную Стефана—Больцмана.

Вводя безразмерные величины ; ;и прологарифмировав, получим

. (1.14)

Полученная зависимость имеет вид , где,,и допускает обработку методом наименьших квадратов (линейной регрессии).