3. Разработка концептуальной модели и ее формализация

   1. Постановка задачи

После анализа задания к курсовой работе приходим к выводу – модель можно представить в виде многоканальной СМО с отказами. Схема модели изображена на рисунке 1.

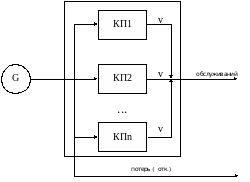
Рисунок 1. Графическая схема модели.

Заявки приходит из источника (G) и занимает любой из свободных каналов. В случае, если все каналы заняты, заявка получает отказ на обслуживание и покидает систему.

В систему поступает простейший поток, т. е. пуассоновский поток заявок на обслуживание с интенсивностью 𝜆, где 𝜆 – число заявок в единицу времени. Заявка, заставшая каналы занятыми, покидает систему. Обслуживание заявки продолжается в течение случайного времени t_обс , распределенного по показательному закону с интенсивностью обслуживания µ = 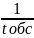. Средняя продолжительность обслуживания одной заявки равна .

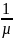Основными характеристиками СМО такого типа являются: абсолютная пропускная способность – А, относительная пропускная способность – q, и вероятность отказа P_отк. Для нахождения этих характеристик СМО рассматривается как физическая система S, которая находится в одном из n+1 состояний.

Для предварительной аналитической оценки СМО можно принять количество каналов обслуживания равное 4.

Выделим для моделируемой СМО состояния исходя из числа заявок, находящихся в обслуживании. В силу отсутствия очереди, их число совпадает с числом занятых каналов. Выделенные состояния:

• S₀ -все каналы свободны;

• S₁ - занят 1 канал, остальные свободны;

• S₂ - заняты 2 канала, один свободен;

• S₃ - заняты 3 канала.

• S₄ - заняты все 4 канала.

На основании данного описания можно построить граф состояний для моделируемой системы (рисунок 2).

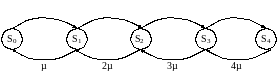
Рисунок 2. Граф состояний для рассматриваемой системы.

На основе графа состояний, можно составим матрицу интенсивности переходов между состояниями системы (рисунок 3).

	S0	S1	S2	S3	S4
S0	- 𝜆	𝜆	0	0
S1	µ	-(𝜆 + µ)	𝜆	0
S2	0	2µ	-(2µ + 𝜆)	𝜆
S3	0	0	3µ	- (𝜆 +3µ)	𝜆
S4	0	0	0	4µ	-4µ

Рисунок 3. Матрица интенсивности переходов.

2. Аналитический расчет смо

Процесс, протекающий в исследуемой СМО, представляет собой частный случай процесса «гибели и размножения». При разработке модели и вычисления ее характеристик учитывается следующее:

• поток событий, поступающих на обслуживание, является простейшим, поток обслуживания подчиняется показательному закону распределения;

• интенсивность обслуживания µ определяется в виде - ;

Для разрабатываемой системы можно представить следующие характеристики:

• проанализировав задание, можно взять число каналов обслуживания n = 4.

Выбор связан с тем, что в систему поступает группа из 3-х заявок, следовательно, меньшее число обслуживающих каналов спровоцирует значительные потери в обработанных заявках;

• средняя продолжительность обслуживания одной заявки описывается математическим ожиданием для показательного закона, со значением 0,2 секунды.

M(t) = ;

Интенсивность поступления заявок на обслуживание – 𝜆 = 5 заявок в секунду.

Значение параметра потока обслуживания – µ = 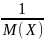= = 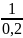5.

Значение приведенной интенсивности потока заявок – ρ = 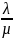= = 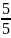1.

На основе полученных характеристик и типа модели СМО, для определения вероятностей состояния системы используется система дифференциальных уравнений (уравнения Колмогорова).

Начальные условия решения системы:

P₀(0) = 1, P₁(0) = P₂(0) = … = P_k(0) = … P_n(0) = 0.

Уравнения Колмогорова для определения вероятностей системы имеют вид:

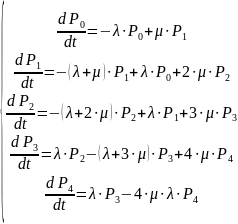
В общем виде система уравнений имеет вид:

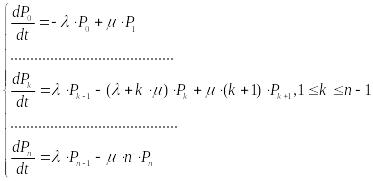
По матрице интенсивности переходов можно составить уравнение, используя мнемоническое правило для определения вероятности состояний:

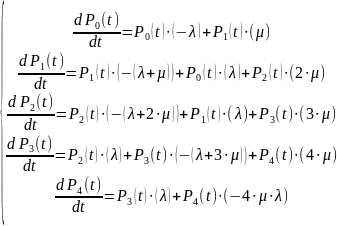
Можно найти решение системы для любого t, но при .

Составим систему уравнений, используя формулу:

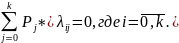
Она примет вид:

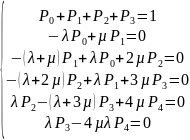
Вместо решения системы уравнений в данном случае можно воспользоваться формулами для схемы «гибели и размножения», и получить значения предельных вероятностей для каждого состояния системы в установившемся режиме:

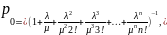
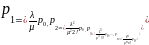
Вводя величину 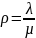, называемую приведенной интенсивностью потока заявок, т. е. среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки, можно получить формулы для расчета предельных вероятностей состояний (при k = 1…n):

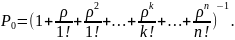
Или в более компактной записи:

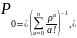
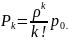
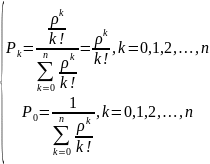
Полученные формулы носят название формулы Эрланга. Они выражают предельные вероятности всех состояний системы в зависимости от параметров n, 𝜆 и µ. Пользуясь ими, можно найти характеристики эффективности СМО: 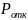, q и A.

Получив формулы, можно найти значения предельных вероятностей для СМО:

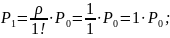
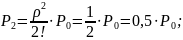
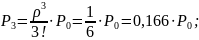
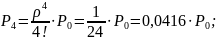
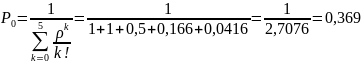
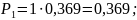
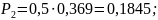
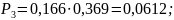
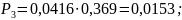
Получив значения предельных вероятностей, стоит проверить их корректность, вычислив значение условия нормировки.

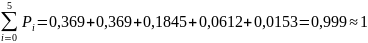
Таким образом, нужно судить о корректности вычисленных значений предельных вероятностей.

Далее вычислим характеристики эффективности СМО:

1. Расчет вероятности того, что все каналы свободны( ).

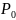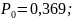
2. Расчет вероятности того, что абоненту будет отказано в обслуживании ( ).

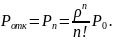
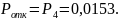
Можно принять данное значение как, удовлетворяющее условию задания.

3. Расчет относительной пропускной способности СМО(q).

Относительная пропускная способность q – это вероятность того, что заявка будет принята к обслуживанию:

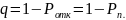
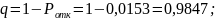
4. Расчет абсолютной пропускной способности СМО (А).

Абсолютная пропускная способность А – это среднее число заявок, обслуженных системой в единицу времени:

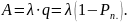
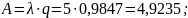
5. Расчет интенсивности отказов обслуживания ( ).

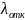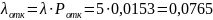
6. Расчет интенсивности потока обслуживания заявок ( ).

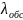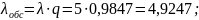
Необходимо проверить соответствие рассчитанных величин интенсивности.

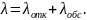
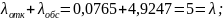
7. Расчет среднего количества занятых каналов .

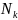Среднее количество занятых каналов можно выразить через абсолютную пропускную способность А, где А есть среднее число заявок, обслуживаемых в единицу времени. Один занятый канал обслуживает в среднем за единицу времени µ заявок, а среднее число занятых каналов:

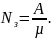
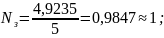
8. Расчет коэффициента загрузки ( ).

Коэффициент загрузки каналов определяется отношением среднего числа занятых каналов к общему числу каналов в системе:

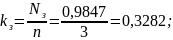
9. Расчет среднего количества свободных каналов ( ).

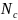Среднее количество свободных каналов определяется как разность общего числа каналов и среднего количества занятых каналов:

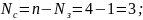
10. Расчет коэффициента простоя каналов( ).

;
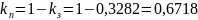