
- •Занятие №1 Первообразная. Неопределенный интеграл.
- •4. Найти интегралы:
- •Занятие №2 Интегрирование методом подстановки
- •11. Найти интегралы:
- •Занятие №3 Интегрирование по частям
- •5. Найти интегралы:
- •Занятия №4-5 Интегрирование рациональных функций методом разложения на простейшие дроби
- •3. Найти интегралы:
- •4. Найти интегралы:
- •5. Найти интегралы:
- •Занятие №6 Интегрирование некоторых иррациональных функций
- •Занятие №7 Интегрирование некоторых классов тригонометрических функций
- •Занятие №8-9 Интеграл Римана
- •Занятие №10 Приложения интеграла Римана
- •1. Вычисление площадей.
- •Занятие №11 Приложения интеграла Римана
- •7. Вычисление площадей поверхности вращения:
- •8. Найти площадь поверхности, полученной вращением кривой:
Занятие №10 Приложения интеграла Римана
1. Вычисление площадей.
1.1
Площадь криволинейной трапеции
 ,
где
,
где
 и непрерывны на отрезке
,
вычисляем по формуле
и непрерывны на отрезке
,
вычисляем по формуле
 .
.
1.2
Аналогично для трапеции
 ,
где
,
где
 и непрерывны на отрезке
и непрерывны на отрезке
 ,
вычисляем по формуле
,
вычисляем по формуле
 .
.
1.3
Площадь криволинейного сектора,
ограниченного лучами
 ,
,
 и кривой
и кривой
 ,
где функция
,
где функция
 непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке
 ,
(
,
( вычисляем по формуле
вычисляем по формуле
 .
.
1.4
Площадь криволинейной трапеции,
ограниченной кусочно-гладкой простой
замкнутой кривой, заданной уравнениями
 ,
где
,
где
 и пробегаемой против часовой стрелки,
вычисляем по формуле
и пробегаемой против часовой стрелки,
вычисляем по формуле
 ,
или
,
или
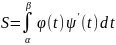 ,
или
,
или
 .
.
2. Найти площади фигур, ограниченных кривыми (сделать чертеж):
1)
 ,
,
 ;
2)
;
2)
 ,
,
 ;
3)
;
3)
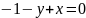 ,
,
 ;
;
4)
 ,
,
 ;
5)
;
5)
 ,
,
 ;
6)
;
6)
 ,
,
 ,
,
 ;
7)
;
7)
 ;
;
8)
 ,
,
 и прямой
и прямой
 ;
9)
;
9)
 ,
,
10)
 ,
и прямой
,
и прямой
 ,
,
 ;
11)
;
11)
 ;
;
12)
 13)
13)
 14)
14)
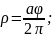 15)
15)

3. Вычисление длины дуги кривой.
3.1
Если кривая задана уравнением
 ,
,
 ,
где
- непрерывно дифференцируемая функция,
то
,
где
- непрерывно дифференцируемая функция,
то
 .
.
3.2
Если кривая задана уравнениями
,
где
,
а
 непрерывно дифференцируемые функции,
то
непрерывно дифференцируемые функции,
то
 .
.
3.3
Если кривая задана уравнением
,
 ,
где
- непрерывно дифференцируемая функция,
то
,
где
- непрерывно дифференцируемая функция,
то
 .
.
4. Найти длину дуги кривой:
1)
 ,
,
 ;
2)
,
;
2)
,
 ;
3)
;
3)
 ,
,
 ;
4)
;
4)
 ;
;
5)
 ,
,
 ;
6)
;
6)
 ,
,
 ;
7)
,
;
;
7)
,
;
8)
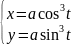 ,
;
9)
,
;
9)
 ,
,
 ;
10)
;
10) 11)
11)
 .
.
Занятие №11 Приложения интеграла Римана
5. Вычисление объема тела вращения
5.1
Объем тела, полученного вращением вокруг
оси
 криволинейной трапеции
криволинейной трапеции
 ,
где
,
где
 непрерывны на отрезке
,
вычисляем по формуле:
непрерывны на отрезке
,
вычисляем по формуле:
 .
.
5.2
Объем тела, полученного вращением вокруг
оси
 трапеции
трапеции
 ,
где
непрерывны на отрезке
,
вычисляем по формуле:
,
где
непрерывны на отрезке
,
вычисляем по формуле:
 .
.
5.3
Объем
тела, образованного при вращении вокруг
полярного луча сектора
,
 , равен:
, равен:
 ,
где
непрерывная при
,
где
непрерывная при
 функция.
функция.
6. Найти объемы тел, полученных при вращении:
1)
Фигуры, ограниченной дугой параболы
 и прямой
и прямой
 ,
вокруг оси
;
,
вокруг оси
;
2)
Фигуры, ограниченной дугой параболы
 ,
отрезком
,
отрезком
 оси
и отрезком прямой
оси
и отрезком прямой
 ,
вокруг оси
;
,
вокруг оси
;
3)
Фигуры, ограниченной одной аркой циклоиды
и отрезком
 оси
,
вокруг оси
;
оси
,
вокруг оси
;
4)
Фигуры, ограниченной дугой логарифмической
спирали
 ,
,
 и полярной осью, вокруг полярной оси;
и полярной осью, вокруг полярной оси;
5)
Фигуры, ограниченной кривой
 ,
вокруг оси
(
,
вокруг оси
( ;
;
6)
Фигуры, ограниченной дугой астроиды
 и отрезками осей координат, вокруг оси
;
и отрезками осей координат, вокруг оси
;
7)
Фигуры, ограниченной кривой
и отрезками прямых
и
 ,
вокруг а) оси
,
б) оси
;
,
вокруг а) оси
,
б) оси
;
8)
Фигуры, ограниченной кривой
 ,
отрезками осей координат и отрезком
прямой
,
отрезками осей координат и отрезком
прямой
 ,
вокруг оси
;
,
вокруг оси
;
9)
Фигуры, ограниченной дугой параболы
 и отрезком прямой
,
вокруг оси
;
и отрезком прямой
,
вокруг оси
;
10)
Фигуры, ограниченной кривой
 и отрезком
и отрезком
 прямой
,
вокруг оси
.
прямой
,
вокруг оси
.
7. Вычисление площадей поверхности вращения:
7.1
Если
 непрерывно дифференцируемая на отрезке
функция, то площадь поверхности,
образованной вращением графика этой
функции вокруг оси
равна:
непрерывно дифференцируемая на отрезке
функция, то площадь поверхности,
образованной вращением графика этой
функции вокруг оси
равна:

7.2
Если
в полуплоскости
 параметрически задана кривая
,
где
,
а
непрерывно дифференцируемые функции,
то площадь поверхности, образованной
при вращении данной кривой вокруг оси
,
равна:
параметрически задана кривая
,
где
,
а
непрерывно дифференцируемые функции,
то площадь поверхности, образованной
при вращении данной кривой вокруг оси
,
равна:

Если
кривая расположена в полуплоскости
 ,
то
,
то
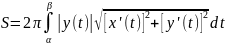 .
.
7.3 При аналогичных условиях площадь поверхности, образованной при вращении кривой вокруг оси соответственно равна:

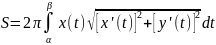 ,
,
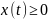
 ,
,

7.4
Площадь
поверхности, образованной вращением
вокруг полярного луча кривой
,
 , равна:
, равна:
 ,
где
непрерывно дифференцируемая при
функция.
,
где
непрерывно дифференцируемая при
функция.
