
- •Занятие №1 Первообразная. Неопределенный интеграл.
- •4. Найти интегралы:
- •Занятие №2 Интегрирование методом подстановки
- •11. Найти интегралы:
- •Занятие №3 Интегрирование по частям
- •5. Найти интегралы:
- •Занятия №4-5 Интегрирование рациональных функций методом разложения на простейшие дроби
- •3. Найти интегралы:
- •4. Найти интегралы:
- •5. Найти интегралы:
- •Занятие №6 Интегрирование некоторых иррациональных функций
- •Занятие №7 Интегрирование некоторых классов тригонометрических функций
- •Занятие №8-9 Интеграл Римана
- •Занятие №10 Приложения интеграла Римана
- •1. Вычисление площадей.
- •Занятие №11 Приложения интеграла Римана
- •7. Вычисление площадей поверхности вращения:
- •8. Найти площадь поверхности, полученной вращением кривой:
Занятие №1 Первообразная. Неопределенный интеграл.
1.
а)
Дайте определение первообразной функции
 .
.
б) Что такое неопределенный интеграл функции ?
в) Назовите свойства неопределенного интеграла.
г) Составьте таблицу основных неопределенных интегралов.
2. Найти первообразную функции , график которой проходит через указанную точку:
а)
 ,
,
 б)
б)
 ,
,
 в)
в)
 ,
,

3. Найти интегралы:
а)
 б)
б)
 в)
в)
 г)
г)
 д)
д)
 е)
е)
 ж)
ж)
 и)
и)
 к)
к)

л)
 м)
м)
 н)
н)
 о)
о)
 п)
п)
р)

4. Найти интегралы:
а)
 б)
б)
 в)
в)
 г)
г)
 д)
д)
 е)
е)

ж)
 з)
з)

5.
Доказать, что если
 ,
то
,
то
 ,
,
 .
.
6. Пользуясь формулой задачи №5, найти интегралы:
а)
 б)
б)
 в)
в)
 г)
г)
 д)
д)
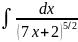 е)
е)
 ж)
ж)

з)
 и)
и)
 л)
л)
 м)
м)
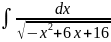 н)
н)

7. Пусть функция
Пусть функция
 является первообразной функции
является первообразной функции
 на все числовой оси. Доказать или
опровергнуть следующие утверждения:
на все числовой оси. Доказать или
опровергнуть следующие утверждения:
а) Если - периодическая функция, то и – периодическая.
б) Если - нечетная функция, то и – четная.
в) Если - четная функция, то и – нечетная.
8.
а)
Доказать, что функция
 не имеет на всей числовой оси ни одной
первообразной.
не имеет на всей числовой оси ни одной
первообразной.
б) Привести пример разрывной функции, для которой на всей числовой оси первообразная существует.
Занятие №2 Интегрирование методом подстановки
9. Доказать формулы:
а) б)
б)

10. Ввести новое переменное и найти интегралы:
а)
 б)
б)
 в)
в)
 г)
г)

 д)
д)
 е)
е)
 ж)
ж) з)
з)
 е)
е)
 и)
и)
 к)
к)

л) м)
м)
11. Найти интегралы:
а)
 б)
б)
 в)
в)
 г)
г)
 д)
д)

е)
 ж)
ж)
 з)
з)
 и)
и)
 к)
к)

12. Подобрав подходящую подстановку, найти интеграл:
а)
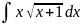 б)
б)
 в)
в)
 г)
г)
 д)
д)
 е)
е)
 ж)
ж)
 и)
и)
 к)
к)
 л)
л)
 м)
м)

н)
 о)
о)
 п)
п)
 р)
р)

Занятие №3 Интегрирование по частям
1.
Запишите формулу интегрирования по
частям. Какие условия на функции
 и
и
 нужно наложить?
нужно наложить?
2.
Интегралы вида:
 ,
,
 ,
,
 ,
где
,
где
 – некоторый многочлен,
– некоторый многочлен,
 – константа.
– константа.
1) 2)
2)
 3)
3)
4) 5)
5)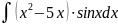 6)
6)
7) 8)
8)
3.
Интегрирование некоторых выражений,
содержащих
 ,
,
 ,
,
 .
.
1) 2)
2)
 3)
3) 4)
4)
 5)
5)

6)
 7)
7) 8)
8) 9)
9) 10)
10) 11*)
11*)
4.
Интегралы вида:
 и
и

5. Найти интегралы:
1)
 2)
2)
 3)
3)
 4)
4)

5)
 6)
6)
 7)
7)
 8)
8) 9)
9)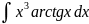
6.* Вывести рекуррентные формулы для вычисления интегралов:
1)
 2)
2) 3)
3)
 4)
4)
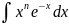
Занятия №4-5 Интегрирование рациональных функций методом разложения на простейшие дроби
1. Какие рациональные функции называются простейшими (элементарными) дробями?
2. Представьте данные выражения в виде суммы простейших дробей с неопределенными коэффициентами:
1)
 2)
2)
 3)
3)
 4)
4)
 5)
5)
 6)
6)
3. Найти интегралы:
1)
 2)
2)
 3)
3)
4)
 5)
5)
 6)
6)
7)
 8)
8)
 9)
9)

