
- •Курс лекций
- •Содержание
- •Введение
- •1 Механическое движение и его виды
- •1 Механическое движение и его виды
- •2 Кинематика поступательного движения
- •3 Кинематика вращательного движения
- •4 Связь между угловыми и линейными величинами
- •Контрольные вопросы
- •1 Динамические характеристики поступательного движения
- •2 Законы Ньютона
- •3 Динамические характеристики вращательного движения
- •Моменты инерции некоторых тел
- •4 Основной закон динамики вращательного движения
- •5 Аналогия формул поступательного и вращательного движений
- •Основные характеристики и формулы кинематики
- •Контрольные вопросы
- •1 Понятие симметрии. Теорема Нетер
- •2 Закон сохранения импульса
- •3 Момент импульса. Закон сохранения момента импульса
- •4 Работа, мощность, энергия
- •5 Закон сохранения энергии
- •Контрольные вопросы
- •1 Принципы относительности Галилея и Эйнштейна
- •2 Понятие о специальной теории относительности
- •3 Основной закон релятивисткой динамики материальной точки
- •4 Закон взаимосвязи массы и энергии
- •Контрольные вопросы
- •Молекулярно-кинетическая теория идеальных газов
- •1 Основные положения молекулярно – кинетической теории
- •2 Опытные законы идеального газа. Уравнение состояния
- •3 Основное уравнение молекулярно-кинетической теории идеальных газов
- •4 Распределение Максвелла
- •5 Барометрическая формула. Распределение Больцмана
- •Контрольные вопросы
- •Основы равновесной термодинамики
- •1 Внутренняя энергия тела и идеального газа
- •2 Работа газа при изменении его объема
- •3 Первое начало термодинамики
- •4 Второе начало термодинамики
- •5 Тепловые двигатели и их кпд
- •Контрольные вопросы
- •Элементы неравновесной термодинамики
- •1 Энтропия как мера беспорядка в системе. Статистический смысл второго начала термодинамики
- •2 Третье начало термодинамики
- •3 Изменение энтропии в открытых системах
- •4 Понятие о самоорганизации
- •5 Примеры самоорганизации в природе
- •Контрольные вопросы
- •Сформулируйте расширенный вариант второго закона термодинамики для открытых систем.
- •Электростатическое поле
- •2 Электростатическое поле и его характеристики
- •3 Теорема Гаусса для электростатического поля в вакууме
- •4 Циркуляция вектора напряженности электростатического поля
- •6 Энергия электростатического поля
- •Контрольные вопросы
- •1 Магнитное поле
- •2 Силы Ампера и Лоренца
- •3 Закон Био – Савара – Лапласа. Простейшие случаи расчета магнитных полей
- •4 Работа по перемещению проводника с током в магнитном поле
- •Контрольные вопросы
- •1 Явление электромагнитной индукции
- •Явления самоиндукции и взаимной индукции
- •3 Магнитное поле в веществе
- •4 Теорема о циркуляции для магнитного поля
- •5 Энергия магнитного поля
- •Контрольные вопросы
- •2 Ток смещения
- •3 Уравнение Максвелла для электромагнитного поля
- •Контрольные вопросы
- •1 Свободные гармонические колебания
- •1 Свободные гармонические колебания
- •2 Затухающие и вынужденные колебания
- •3 Волны
- •4 Электромагнитные волны
- •Контрольные вопросы
- •Волновые свойства электромагнитного излучения
- •1 Развитие представлений и природе света
- •2 Интерференция света и методы ее наблюдения
- •1 Метод Юнга
- •2 Зеркало Ллойда
- •3 Интерференция в тонких пленках
- •3 Дифракция электромагнитных волн
- •4 Поляризация света
- •Контрольные вопросы
- •Квантовые свойства электромагнитного излучения
- •1 Тепловое излучение. Гипотеза Планка
- •2 Фотоэффект и его применение
- •3 Давление света. Фотоны
- •4 Эффект Комптона
- •5 Единство волновых и корпускулярных свойств электромагнитного излучения
- •Контрольные вопросы
- •1 Гипотеза де Бройля. Корпускулярно волновой дуализм как универсальное свойство материи
- •2 Соотношение неопределенностей
- •3 Волновая функция и ее статистический смысл
- •4 Уравнение Шредингера и его решения для ряда простейших случаев
- •1 Движение свободной частицы
- •2 Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими стенками
- •Контрольные вопросы
- •1 Развитие представлений о строении атома
- •2 Атом водорода в квантовой механике
- •3 Многоэлектронные атомы
- •4 Атомное ядро
- •5 Радиоактивность. Радиоактивные излучения
- •Контрольные вопросы
- •Современная физическая картина мира
- •1 Агрегатные состояния вещества
- •2 Кристаллы и их симметрия. Дефекты в кристаллах
- •3 Понятие о зонной теории твердых тел
- •4 Проводимость твердых тел. Проводники, полупроводники и диэлектрики
- •Контрольные вопросы
- •2 Частицы и античастицы
- •3 Элементарные частицы и их классификация. Понятие о кварках
- •1 Основные типы физических взаимодействий в природе
- •2 Частицы и античастицы
- •3 Элементарные частицы и их классификация. Понятие о кварках
- •4 Современная физическая картина мира
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Перечень ключевых слов
2 Затухающие и вынужденные колебания
Реальные свободные колебания всегда являются затухающими, т.к. энергия колебаний с течением времени уменьшается (расходуется на работу против силы трения, выделяется на активном сопротивлении в виде тепла и т.д.).
Характер затухающих колебаний определяется быстротой потери энергии. Можно показать, что затухающие колебания в линейных системах описываются дифференциальным уравнением
![]() . (12.3)
. (12.3)
Решением этого уравнения является выражение
![]() .
(12.4)
.
(12.4)
Здесь A0
– амплитуда колебаний в начальный
момент времени, β – коэффициент затухания.
Величину
![]() можно рассматривать как амплитуду
колебания, зависящую от времени.
Графически такое колебание изображено
рисунке 14.
можно рассматривать как амплитуду
колебания, зависящую от времени.
Графически такое колебание изображено
рисунке 14.
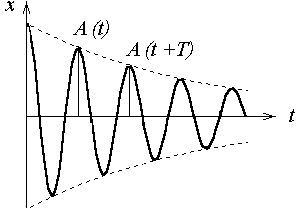
Рисунок 14 - Затухающее колебание
Для описания затухающих колебаний принято использовать логарифмический декремент затухания.
Логарифмический декремент затухания – логарифм отношения двух следующих друг за другом максимальных отклонений колеблющейся величины в одну и ту же сторону:
![]() . (12.5)
. (12.5)
Легко получить
связь логарифмического декремента
затухания с коэффициентом затухания:
![]() .
.
Для получения в
реальной системе незатухающих колебаний
потери энергии необходимо компенсировать.
Такая компенсация возможна с помощью
какого–либо периодически действующего
фактора X(t),
изменяющегося
по гармоническому закону
![]() .
В теории
колебаний этот фактор называется
вынуждающей
силой.
При рассмотрении механических колебаний
роль X(t)
играет внешняя вынуждающая сила, в
электрическом колебательном контуре
роль X(t)
может играть внешняя подводимая к
контуру ЭДС или переменное напряжение.
.
В теории
колебаний этот фактор называется
вынуждающей
силой.
При рассмотрении механических колебаний
роль X(t)
играет внешняя вынуждающая сила, в
электрическом колебательном контуре
роль X(t)
может играть внешняя подводимая к
контуру ЭДС или переменное напряжение.
Колебания, происходящие под действием внешнего периодически действующего фактора, называются вынужденными.
Характер вынужденных колебаний зависит от действующих в колебательной системе внутренних сил и внешней периодической силы X(t). Для выяснения характера колебаний решают дифференциальное уравнение для конкретной колебательной системы.
Графически процесс установления вынужденных колебаний представлен на рисунке 15.
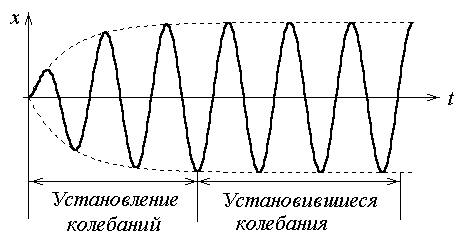
Рисунок 15 – Установление вынужденных колебаний
В установившемся режиме вынужденные колебания происходят с частотой Ω (с частотой вынуждающей силы) и являются гармоническими.
Представляет интерес зависимость амплитуды A вынужденных колебаний от частоты вынуждающей силы (рисунок 16). Эта зависимость имеет максимум; частота, при которой наблюдается максимум амплитуды, называется резонансной частотой.
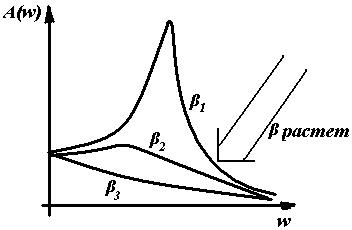
Рисунок 16 – Явление резонанса
Явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к резонансной называется резонансом. При малом затухании в системе резонансная частота практически совпадает с собственной частотой колебательной системы.
На рисунке 16 представлены резонансные кривые для колебательных систем с разным коэффициентом затухания β. Видно, что возрастание амплитуды колебаний в системе тем больше, чем меньше коэффициент затухания.
Явления резонанса могут быть как полезными, так и вредными. Например, при конструировании машин и различных сооружений необходимо, чтобы собственная частота их колебаний не совпадала с частотой возможных внешних воздействий. В противном случае могут возникнуть вибрации, приводящие к серьезным разрушениям. С другой стороны, явление резонанса позволяет обнаружить даже очень слабые колебания, если совпадают с частотой собственных колебаний прибора. Явление резонанса широко используется в прикладной акустике, в радиотехнике, в электротехнике.
