2 Кинематика поступательного движения

Рассмотрим движение материальной точки вдоль произвольной кривой (рисунок 2).

Перемещение – вектор, соединяющий начальную (1) и конечную (2) точки траектории, по которой двигалась материальная точка некоторый промежуток времени. Траектория – линия, описываемая при движении материальной точкой в пространстве. В зависимости от формы траектории движение бывает прямолинейным или криволинейным.

Путь – сумма длин отрезков траектории.

Рисунок 2 – Определение пути и перемещения

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути Δs.

Для характеристики движения материальной точки вводится векторная величина – скорость, которая определяет быстроту и направление движения. Модуль скорости равен производной пути по времени:

. (1.2)

Мгновенная скорость направлена по касательной к траектории. В системе СИ скорость измеряется в м/с.

Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение:

(1.3)

Скорость тела может изменяться как по величине (модулю), так и по направлению. Вектор ускорения принято представлять в виде двух составляющих: тангенциальной и нормальной (Рисунок 3).

Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю:

. (1.4)

Тангенциальное ускорение направлено по касательной к траектории параллельно вектору скорости в случае ускоренного движения и в противоположную сторону в случае замедленного.

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение направлено к центру кривизны траектории и численно равно

, (1.5)

где R  радиус кривизны траектории в данной точке.

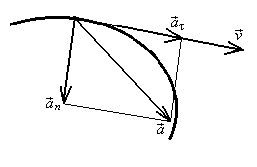
Рис.4

Рисунок 3 – Определение составляющих ускорения

(движение ускоренное)

Векторы нормального и тангенциального ускорений направлены перпендикулярно друг другу. Вектор полного ускорения

, , (1.6)

В зависимости от значений тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

1) а_τ=0, а_n=0 − прямолинейное равномерное движение;

2) а_τ=а=const, а_n=0 − равнопеременное прямолинейное движение. Можно показать, что при таком движении справедливы соотношения:

v=v₀±at, s=v₀t±at²/2. (1.7)

Здесь знак «плюс» берется в случае равноускоренного движения, а знак «минус» − в случае равнозамедленного движения.

3) а_τ= f(t), а_n=0 − прямолинейное движение с переменным ускорением;

4) а_τ=0, а_n=const − движение по окружности с постоянным численным значением скорости.

Существуют более сложные типы движения, примеры которых будут рассмотрены на практических занятиях.

3 Кинематика вращательного движения

При вращательном движении твердого тела вокруг неподвижной оси все точки тела описывают окружности разных радиусов, центры которых находятся на оси вращения. Все точки тела движутся с разными линейными скоростями и ускорениями и проходят за одно и то же время разные пути. При этом угол поворота, угловая скорость и угловое ускорение для всех точек тела оказываются одинаковыми.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

(1.8)

где   угол поворота. Направление угловой скорости определяется по правилу правого винта (рисунок 4). В СИ угловая скорость измеряется в рад/с.

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

(1.9)

Направление вектора углового ускорения определяется по следующему правилу: при ускоренном движении направление углового ускорения совпадает по направлению с направлением угловой скорости, а при замедленном движении направление угловой скорости антипараллельно направлению угловому ускорению.

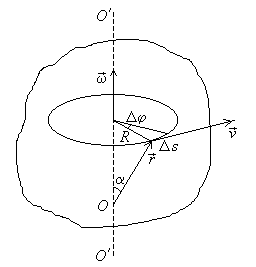
Рисунок 4 – Вращение тела вокруг неподвижной оси

Если угловая скорость ω постоянна, то вращение является равномерным и его можно характеризовать периодом вращения T – временем, за которое точка совершает один полный оборот. Легко показать, что T=2π/ω.

Число полных оборотов, совершаемых телом за единицу времени, называется частотой вращения n.

N=1/ T= ω/(2 π), ω=2πn. (1.10)

При вращении с постоянным угловым ускорением справедливы соотношения

ω=ω₀±εt, φ=ω₀t±εt²/2. (1.11)

Обращаем внимание на аналогию соотношений (1.11) и (1.7).