2 Силы Ампера и Лоренца

Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током I, равна:

dF= I dlBsinα или . (9.4)

Направление вектора силы Ампера может быть найдено по правилу левой руки.

Закон Ампера позволяет определить единицу магнитной индукции B. Предположим, что элемент проводника dl с током I перпендикулярен направлению поля. Тогда действующая на него сила будет максимальной (sinα=1). При этом для модуля вектора магнитной индукции будет справедливо выражение

. (9.5)

Модуль вектора магнитной индукции численно равен максимальной силе Ампера, действующей на проводник длиной 1 м с током 1 А. Единица магнитной индукции – тесла (Тл). 1 Тл – магнитная индукция такого однородного магнитного поля, которое действует с силой 1Н на каждый метр длины прямолинейного проводника, перпендикулярного магнитному полю.

Опыт показывает, что магнитное поле действует не только на проводник с током, но и на отдельные заряды, движущиеся в этом поле. Сила, действующая на заряд q, движущийся в магнитном поле со скоростью v, называется силой Лоренца:

dF= qvBsinα или . (9.6)

Здесь α – угол между направлением магнитного поля и скоростью заряда. Направление вектора силы Лоренца, действующей на положительный заряд, может быть найдено по правилу левой руки. На отрицательный заряд сила Лоренца действует в противоположном направлении.

Сила Лоренца всегда перпендикулярна направлению движения частицы, поэтому она не совершает работы. Сила Лоренца изменяет только направление движения заряженной частицы, модуль скорости при этом остается постоянным.

3 Закон Био – Савара – Лапласа. Простейшие случаи расчета магнитных полей

Французские физики Био и Савар в 1820 г. провели исследования магнитных полей проводников с током различной формы. Они установили, что магнитная индукция пропорциональна силе тока и зависит от расстояния до точки, где определяется _.

_{Обобщая их экспериментальные данные, французский математик Лаплас предложил формулу, по которой можно вычислить вектор магнитной индукции поля, создаваемого элементом проводника dl с током I в некоторой точке А, расположенной на расстоянии r от этого элемента (Рис.11).} Это соотношение получило название закона Био – Савара – Лапласа:

или (9.7)

Здесь ₀- магнитная постоянная,  - магнитная проницаемость вещества, – вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, – радиус-вектор, проведенный от элемента проводника в точку наблюдения, – модуль радиуса-вектора (рисунок 11).

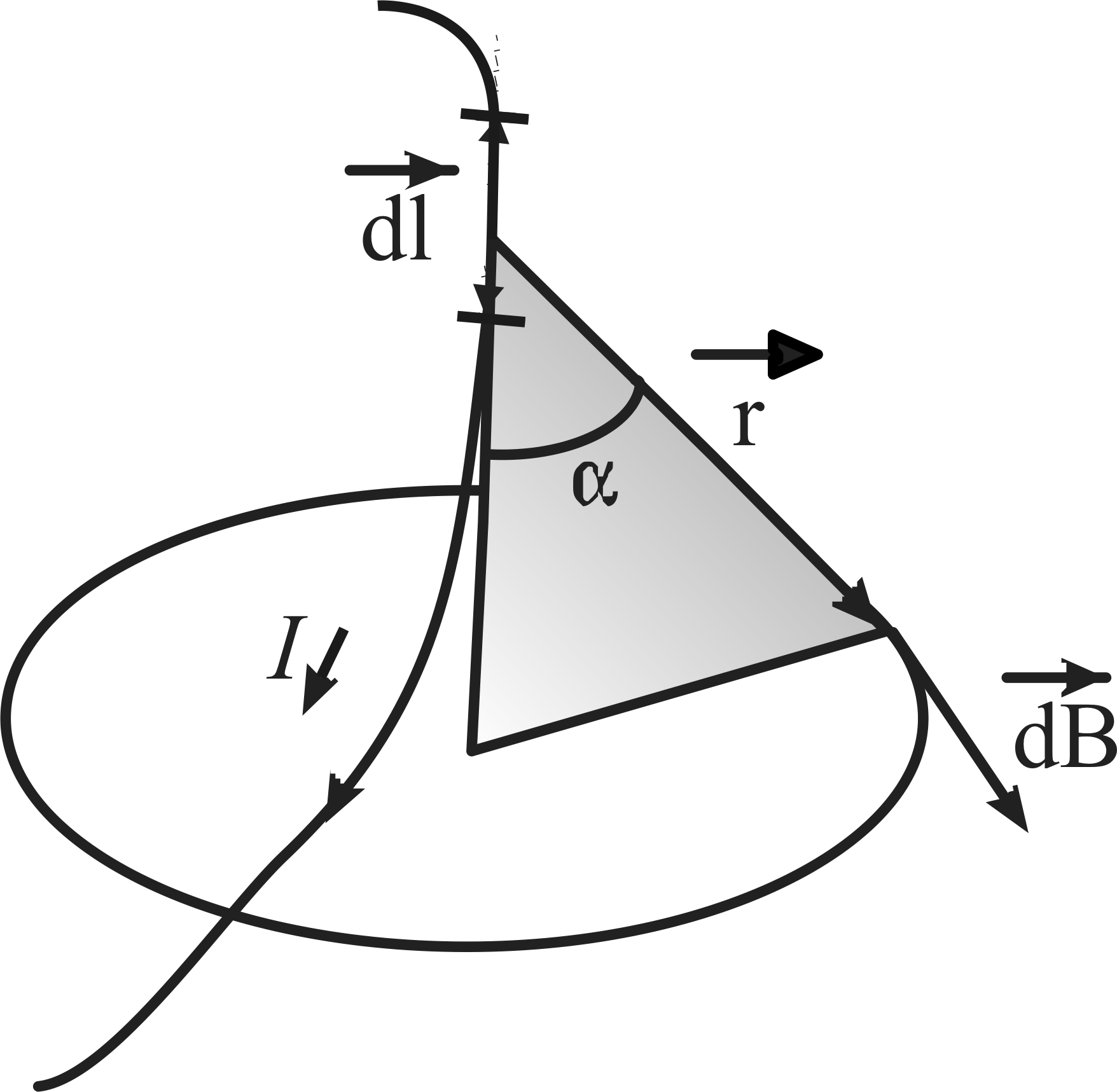
Рисунок 11 – Магнитное поле элемента тока

В соответствии с принципом суперпозиции магнитное поле проводника с током может быть вычислено как векторная сумма полей, создаваемых отдельными его участками:

. (9.8)

Интегрирование производится по всей длине проводника l.

Используя закон Био – Савара – Лапласа, можно вычислить магнитные поля любых проводников с током. Приведем формулы для ряда важных простейших случаев.

Источник магнитного поля	Формула для вычисления магнитной индукции
Круговой виток радиуса R с током I	В центре витка	B=0I/2R
Бесконечный прямолинейный провод с током I	На расстоянии r от проводника	B=0I/2πr
Соленоид длиной l c числом витков N с током I	В центре cоленоида	B=0IN/l
Тороид c числом витков N радиусом r с током I	В центре тороида	B=0IN/(2πr)