3 Основное уравнение молекулярно-кинетической теории идеальных газов

Основное уравнение МКТ выводится для одноатомного идеального газа в предположении, что молекулы движутся хаотически, число столкновений молекул между собой пренебрежимо мало по сравнению с числом их ударов о стенки сосуда, а последние являются упругими. Вывод уравнения сделан еще в школьном курсе физики, уравнение имеет вид:

(5.6)

где Р – давление идеального газа на стенку сосуда; n – концентрация (число молекул в единице объема) молекул газа; m – масса молекулы газа;

<υ²> - средняя квадратичная скорость молекул.

Сравнивая выражения (5.2) и (5.6) можно получить очень важное соотношение:

(5.7)

где <Е> - средняя кинетическая энергия отдельной молекулы;

Из выражения (5.7) следуют важные выводы:

1. абсолютная температура является мерой кинетической энергии поступательного движения молекул;

2. абсолютному нулю температуры (0 К) отвечает равная нулю кинетическая энергия молекул.

4 Распределение Максвелла

Молекулы газа движутся хаотически. В результате многократных столкновений скорость каждой молекулы постоянно изменяется по величине и направлению. Однако, в состоянии равновесия в газе устанавливается некоторое стационарное (не меняющееся со временем) распределение молекул по скоростям.

Статистические методы позволяют найти функцию распределения молекул по скоростям, а также распределение числа молекул по кинетическим энергиям их беспорядочного теплового движения. Впервые это сделал К. Максвелл (1831 – 1879 г.г.), поэтому найденные им выражения называют функциями распределения Максвелла.

Максвелл ввел функцию f(u,T)

(5.8)

где (dN/N) – относительное число молекул, скорости которых заключены в интервале (v, v+dv). Тогда (dN/(Ndv)) – относительное число молекул в указанном интервале скоростей, приходящееся на единичное значение этого интервала.

Применяя методы теории вероятностей, Максвелл нашел функцию f(v,T).

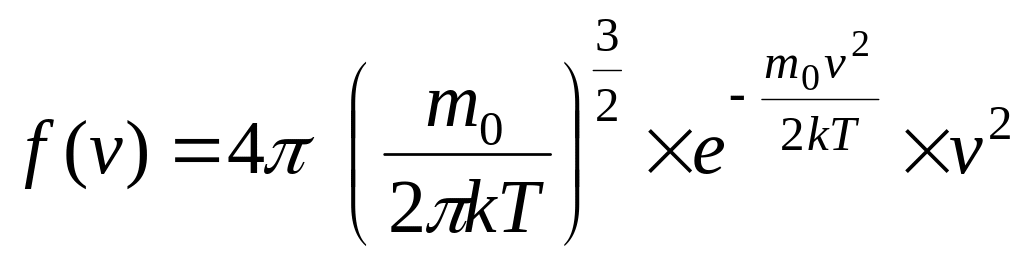. (5.9)

Функция f(v) представлена на рисунке 5.

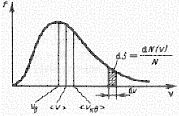
Рисунок 5 – Кривая распределения молекул по скоростям

Видно, что эта функция имеет максимум при определенной скорости v_кв, которая называется наиболее вероятной. Значение наиболее вероятной скорости можно получить, исследуя функцию (5.9) на экстремум. Соответствующие вычисления приводят к следующему результату:

(5.10)

Очевидно, что v_кв. зависит от массы молекулы m₀: более тяжелые молекулы при прочих равных условиях движутся медленнее. С повышением температуры средняя квадратичная скорость молекул возрастает (рисунок 6).

При этом доля молекул, обладающих этой скоростью, уменьшается. Площадь, ограниченная кривой распределения, остается неизменной (при повышении температуры кривая растягивается, значение максимума уменьшается). Это связано с тем, что площадь под кривой распределения характеризует общее число молекул N, которое остается неизменным.

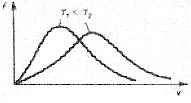
Рисунок 6 – Кривые распределения молекул по скоростям

при различных температурах

Закон Максвелла о распределении молекул идеального газа по скоростям можно представить через энергии теплового движения молекул. Пусть dN(ε) – число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от до . Тогда функция распределения молекул по энергиям теплового движения имеет вид:

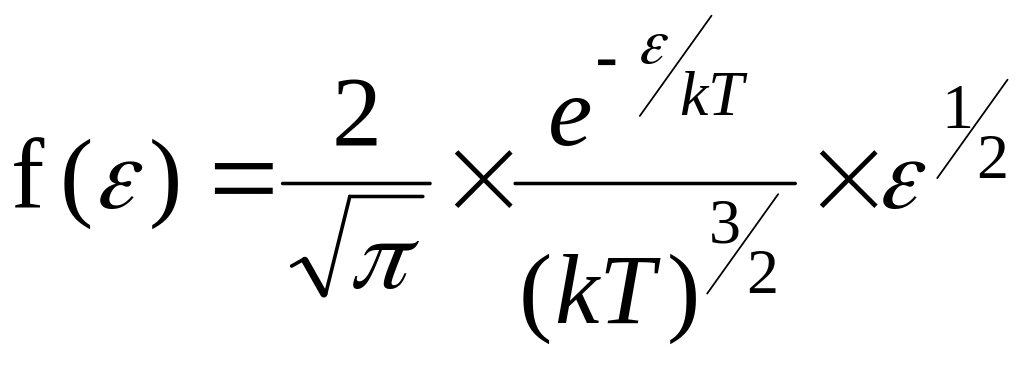(5.11)