1.3 Количество скольжения, плотность дислокаций

Общее увеличение среднего смещения дислокаций называется количеством скольжения, которое происходит за время 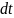и соответствует

(4)

Где - приращение плоскости сдвига за время ;

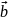– вектор Бюргерса;

- общая длина всех линий дислокаций;

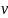- общий обьем;

- среднее смещение дислоаций;

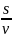- плотность дислокаций

Сила действующая на единицу длины дислокации

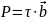(5)

Где 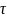- касательное напряжение сдвига.

1.4 Вектор Бюргерса

Наибольшее искажение решетки имеет место в центре самой дислокации. То есть в ядре дислокаций, около двух меж атомных расстояний. Мерой искажения решетки, а так же, мерой величины дислокационного сдвига является вектор Бюргерса. Вектор характеризует Энергию дислокаций и действие на ее силы. Вектор Бюргерса – это отрезок замыкающий разрыв петли особого рода называемый контуром Бюргерса.

Контур Бюргерса строится путем последовательного обхода против часовой стрелки от атома к атому для части кристаллической решетки с дислокацией (рисунок 6а).Для идеального кристалла делается такой же обход, со счетом атомов так же как и у решетки с дислокациями (рисунок 6б).

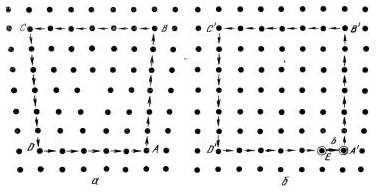
а) решетка с дислокацией б) решетка без дислокации

Рисунок 6 – Построение контура и вектора Бюргерса.

Вектор Бюргерса можно разложить по базисным векторам решетки:

,

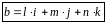где - базисные векторы кристаллической решетки, совпадаю- щие с направлениями ребер элементарной ячейки;

- символы кристаллографического направления решетки.

Если 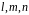равны 0, 1, 2…, то есть целым числам, то такие дислокации называют полными; если не являются целыми числами, то дислокации называют неполными или частичными.

Таким образом, дислокации могут быть:

- Единичные (дислокации единичной мощности), когда вектор Бюргерса равен одному межатомному расстоянию (то есть, - параметру решетки); эти дислокации обязательно являются полными ( );

- Частичные, когда вектор Бюргерса меньше параметра решетки ( );

- Кратные или супердислокации, когда вектор Бюргерса превышает

параметр решетки

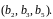
В качестве примера на рисунке 7 показана ГЦК решетка с вышеупомянутыми векторами Бюргерса.

Для краевой дислокации вектор Бюргерса перпендикулярен оси (линии) дислокации, а для винтовой дислокации – параллелен оси дислокации.[4]

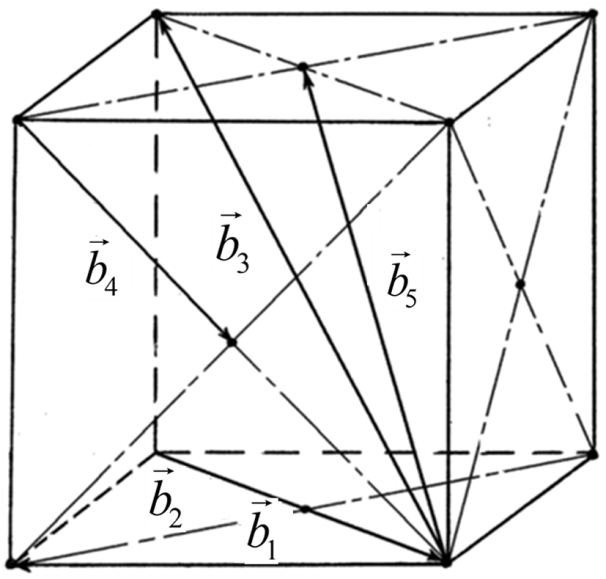
- единичная дислокация; - частичная дислокация;

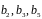- кратные или супердислокации.

Рисунок 7 – Векторы Бюргерса в ГЦК решетке.

1.5 Зависимость сопротивления пластическому сдвигу от количества дефектов кристаллической решетки.

Для уменьшения эффекта упрочнения необходимо наличие дислокаций и условий способствующих их образованию, в процессе деформации. Дефекты кристаллической решетки ослабляют, но одновременно, они затрудняют движение дислокаций, что приводит к упрочнению металла. Это обстоятельство используют при шлифовании металла. Поскольку, при образовании твердого раствора происходит упругое искажение решетки, что затрудняет движение дислокации. Увеличение числа дислокаций в процессе деформации, также приводит к упрочнению металла.[4]