2.4. Диффузия вихревого слоя

Модель вихревого слоя

Рассмотрим случай движения неограниченного объема жидкости, имеющей в начальный момент времени следующее распределение скоростей (U=const)

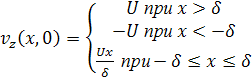
Слой жидкости является вихревым слоем, вектор завихренности которого равен

.

Вне этого слоя течение жидкости безвихревое.

Ограничимся исследованием наиболее простого случая вихревого слоя, когда . При этом можно записать

Для решения этой задачи можно воспользоваться формулой ()

представив функцию как функцию аргумента так

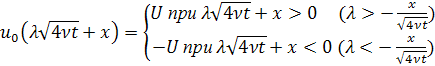
Имеем

Совершим замену переменных в первом интеграле, положив

Формула преобразуется к виду (штрих опущен)

По теореме Ньютона интегралы можно объединить. В результате получаем

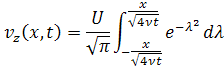
или

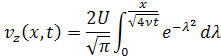
Интеграл, вошедший в последнюю формулу, выражается через интеграл вероятностей

Функция обладает свойствами, вытекающими из ее определения

Запишем формулу для распределения скоростей в задаче о диффузии вихревого слоя через функцию интеграл вероятности

Определим теперь поле вихрей в жидкости в любой момент времени Согласно формуле () можем записать

что дает возможность найти распределение завихренности в жидкости

-

Как следует из полученной формулы, завихренность, сосредоточенная изначально только в окрестности плоскости x=0, мгновенно распространяется на всю жидкость при t>0, cсохраняясь все время наибольшей в окрестности плоскости x=0.

Однако в других точках потока с координатами максимум завихренности достигается не сразу, а через определенный промежуток времени, и тем больший, чем дальше отстоят эти точки от начального вихревого слоя. В этом убеждаемся, находя максимум завихренности в точках с координатой , в зависимости от времени. Составляем уравнение Имеем

[

Корнем полученного уравнения является

Максимум завихренности в соответствующих точках при этом равен

Как следует из формул () и (), промежуток времени достижения максимума завихренности в точках с координатами растет по квадратичному закону в зависимости от удаленности точек жидкости от первоначального вихревого слоя и обратно пропорционален вязкости жидкости - тем меньше, чем больше вязкость жидкости. Максимальная же завихренность в точках с координатой не зависит от вязкости жидкости и обратно пропорциональна удаленности от первоначального вихревого слоя.

2.5. Использование найденных решений для исследования других нестационарных задач

Линейная комбинация решений

Уравнение () является линейным и поэтому сумма его частных решений является тоже его решением. Если к тому же возможно найти физически разумные краевые и начальные условия, которым удовлетворяет такое решение, то можно считать такое решение точным решением соответствующей новой задачи.

Рассмотрим комбинацию решения () задачи о диффузии вихревого слоя

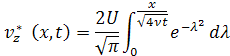
и тривиальное решение

Составим линейную комбинацию этих решений

= -

Рассмотрим область . При во всей этой области согласно формуле () . Однако при и всех имеем . Эти свойства функции свидетельствуют о том, что жидкость а в полупространстве , изначально покоившаяся, приводится в движение плоскостью как твердой плоскостью, получившей мгновенную скорость в направлении оси Oz и сохраняет ее во все время движения. Следовательно, мы имеем решение задачи о течении жидкости, вызванном движением в ней плоскости, мгновенно приведенной в движение и сохраняющей все время постоянную скорость Формула () дает решение для полупространства . Для полупространства при этом течение будет симметричным.

Решения, получаемые дифференцированием известных решений

Если функция удовлетворяет уравнению (), то этому уравнению будет удовлетворять и функция . Это позволяет построить решение новой задачи – о разгоне покоящейся жидкости, занимающей полупространство, постоянной силой трения, приложенной к его границе.

Рассмотрим задачу

Покоящаяся тяжелая вязкая жидкость занимает полупространство и имеет свободную границу, к которой приложено постоянное давление . С момента t=0 к свободной поверхности прикладывается постоянная сила трения T, направленная в сторону z>0. Требуется определить возникающее при этом течение жидкости. Такая задача представляет определенный интерес для объяснения возникновения течений жидкости под действием ветра. Соответствующая математическая задача одномерная и ставится так

Найти решение уравнения

при граничных и начальных условиях

где нормаль n направлена в ту сторону жидкости, с которой производится воздействие на поверхность. В рассматриваемом случае . Поэтому граничное условие надо записать так

Воспользуемся тем фактом, что функция

удовлетворяет уравнению

и начальному уcловию

так как в покоящейся жидкости касательные напряжения отсутствуют

Граничные условия имеют вид

Сопоставляя формулы () и (), убеждаемся, что функция с точностью до обозначений функция совпадает с функцией ().Поэтому можем записать

Учитывая значение функции (), получаем уравнение для определения поля скоростей в жидкости

Учитываем теперь, что

Вычислим вторую производную от по

При этом , пользуясь уравнением (), находим

Интегрируя это уравнение по с учетом начального условия , получаем

Из этого решения следует, что частицы жидкости, находящиеся на поверхности обладают скоростью

Это же значение скорости достигается всеми остальными частицами жидкости с ростом времени, так как для любого конечного подынтегральная функция является растущей от нуля функцией, ведущей себя как при Поэтому при больших имееем

В процессе роста со временем скорости внутри жидкости всегда найдется момент времени, когда в заданной точке жидкости с координатой скорость достигнет половинной скорости на ее границе . Этот момент времени можно найти исходя их условия

которое приводит к уравнению

()

Вычислением интеграла для каждого численного значения без особого труда находится соответствующее значение , при котором выполняется последнее равенство. Отметим, что после замены переменных

.

,

уравнение () сводится к такому

,

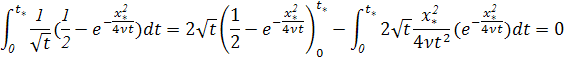
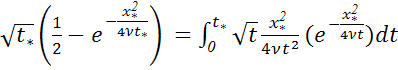
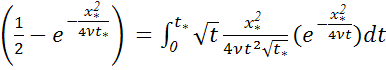
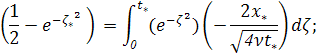
Написать Maple-программу

2.6.. Диффузия вихрей в вязкой жидкости

Диффузия вихревой нити

Рассматриваем прямолинейную вихревую нить, с которой связываем ось Oz цилиндрической системы координат . ( 1/ Принимаем, что в начальный момент времени t=0 поле скоростей в жидкости определяется формулами

В силу осевой симметрии допускаем, что при t >0 течение сохраняет осевую cимметрию

,

,

Как было установлено, завихренность распространяется мгновенно на всю жидкость.

В рассматриваемом случае , ,

Исследование диффузии вихрей удобно провести на основе уравнения Гельмгольца для вихрей

Учитываем, что , )

В рассматриваемом случае это приводит к уравнению

откуда следует