1.3. Постановка задач о неустановившихся течениях однородной несжимаемой жидкости с постоянной вязкостью
В случаях вязких однородных несжимаемых жидкостей с постоянной вязкостью постановки задач о неустановившемся течении существенно упрощаются, так как система уравнений, включающая уравнение неразрывности и уравнения движения, оказывается замкнутой системой уравнений, которая может быть решена независимо от уравнения баланса энергии, если граничные и начальные условия (1.3)-(1.8) не зависят от температуры. Не нарушая общности, ограничиваемся записью уравнений в декартовых координатах.
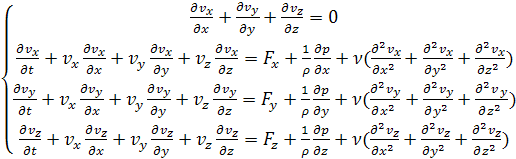(1.10)
По найденным в результате решения начально-краевой задачи (1.2)- (1.5), (1.10) полям скоростей и давлений в потоке жидкости поле температур в потоке при необходимости можно определять из уравнения баланса энергии
(1.11)
где 
,
При решении уравнения (1.11) надо выполнять начальные условия (1.7) и краевые условия (1.8) или (1.9).
МОДУЛЬ 2. Неустановившиеся одномерные течения вязкой однородной несжимаемой жидкости
2.1. Основные уравнения одномерных течений
Многомерность
и нелинейность исходных уравнений
являются практически непреодолимыми
препятствиями для построения точных
аналитических решений трехмерных задач
о неустановившихся течениях вязких
жидкостей и газов. Эти препятствия
ослабевают с уменьшением размерности
пространства. Наиболее простые уравнения
движения получаются в случае задач о
неустановившемся течении однородной
несжимаемой жидкости с прямолинейными,
параллельными траекториями всех частиц
жидкости. Такие потоки являются
одномерными в декартовых координатах,
если одну из осей координат направить
параллельно направлению движения частиц
жидкости. Пусть, для определенности,
это будет ось Oz.В
этой системе координат будет отлична
от нуля только одна компонента скорости
- 
,
а из уравнения неразрывности будет
следовать , что 
,
При этом 
и уравнения движения жидкости принимают
вид [ ]
(2.1)
(2.2)
Произведем дальнейшее упрощение постановки задачи и примем что течения во всех плоскостях, перпендикулярных оси Oy идентичны, что дает возможность принять
(2.3)
Уравнения преобразуются к виду
(2.4)
(2.5)
Неустановившиеся одномерные течения могут быть безнапорными, если
тогда имеем дело с неустановившимся течением жидкости, описываемым однородным одномерным уравнением теплопроводности
(2.6)