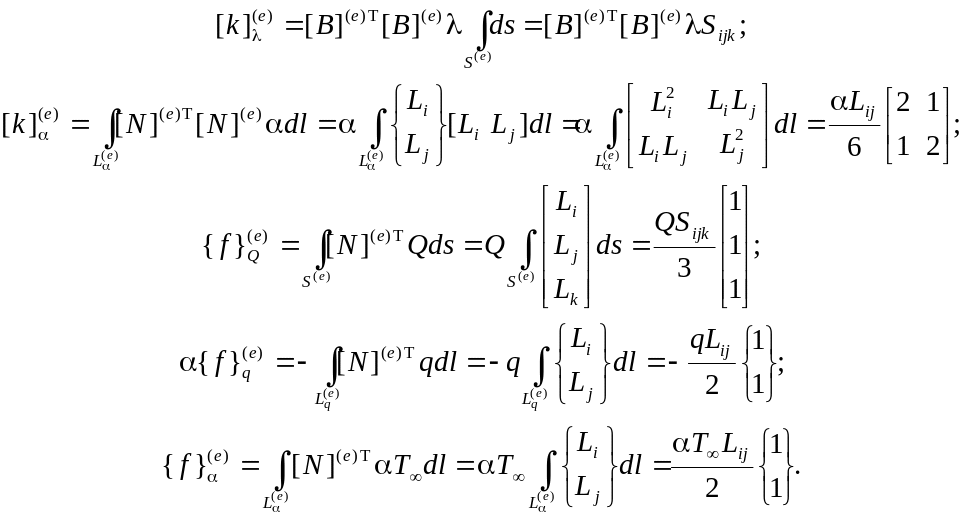Метод Галеркина

Рассмотрим дифференциальное уравнение, описывающее в исследуемой области V некоторый физический процесс:

L(U)  0,

где L() – дифференциальный оператор; U – искомая функция.

Далее, разбивая исследуемую область V на конечные элементы, переходим от искомой функции U к кусочно-гладкой U заданной в области на V в общем случае не совпадающей с V:

Так как искомое решение U является приближенным, то L(U)    0, где  – ошибка (невязка) решения.

В методе Галеркина ошибку минимизируют, приравнивая нулю ее проекцию на функцию формы:

или

(1)

Так как задать математически финитную функцию сложно, интеграл в (1) представляют суммой интегралов в пределах КЭ.

Теперь ненулевое значение функций формы вне КЭ несущественно.

Критерий ограниченной сходимости

Условием сходимости МКЭ является представление функции формы конечного элемента полиномом как минимум р-ой степени, где р – наивысший порядок производной входящей в (1). Так как обычно используют линейную интерполяцию на КЭ, то в (1) допускаются лишь первые производные.

Уравнение (1) обычно представляет собой систему алгебраических уравнений относительно узловых значений искомой функции U. Матричная запись системы имеет вид:

[K]{U}  {F},

где – матрица коэффициентов системы уравнений МКЭ;

– вектор свободных членов системы уравнений МКЭ;

{k}^(e) и {f}^(e) – соответственно матрица коэффициентов и вектор свободных членов конечного элемента

Завершающим этапом формирования системы уравнений МКЭ (разрешающей системы) является учет главных граничных условий (ГУ первого рода). Если U_i  C, то в системе производятся следующие изменения:

где М – очень большое число.

Естественные граничные условия (ГУ второго – четвертого родов) учитываются в (1).

Решение двумерной стационарной задачи теплопроводности методом конечных элементов

Для вывода разрешающей системы воспользуемся методом Галеркина.

Распределение температуры подчиняется уравнению теплопроводности:

Сделаем допущение, что все точки среды неподвижны относительно выбранной системы координат. Тогда, с учетом того, что задача стационарная и плоская, уравнение упростится:

Применив метод Галеркина, получим следующую систему:

(1)

Однако, так как в подынтегральное выражение входят вторые производные, мы не сможем использовать линейные функции формы. Поэтому произведем снижение порядка производных.

Интеграл от первого слагаемого можно разложить следующим образом:

(2)

В справедливости такого разложения легко убедиться, если рассмотреть следующее равенство

Интеграл от второго слагаемого в (1) разложится аналогично (2). Для дальнейшего упрощения воспользуемся формулами:

(3)

(4)

где U – произвольная функция, зависящая от x и y.

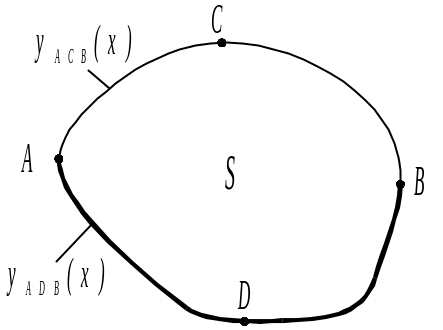
Формула (4) выводится следующим образом. Пусть область S имеет простейшую форму (рисунок). Тогда будут справедливы следующие преобразования.

где L ­– контур, ограничивающий область S. Без доказательства отметим, что данная формула будет справедлива для областей любой формы

Таким образом, Аналогично получается формула (3)

С учетом всех преобразований систему (1) можно записать в виде:

(5)

Так как T = [N]{T}, выражение, входящее во второй интеграл системы (5), можно преобразовать:

где [B] = {grad}[N] – матрица градиентов. Вектор-столбец {grad} – матричный аналог вектора-градиента

Вид системы (5) еще более упростится:

(6)

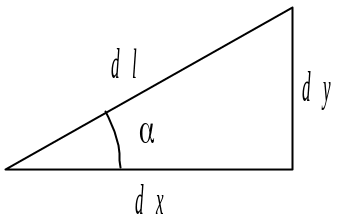
Преобразуем первый интеграл, входящий в (6). Для этого подынтегральное выражение умножим и разделим на элементарный отрезок Получим

С учетом рисунков, можно записать:

Последнее преобразование является определением производной по направлению.

Итак, первый интеграл системы (6) примет вид:

Так как в подынтегральном выражении есть произведение вида T/n, т.е. поток тепла из области S, то с помощью этого интеграла можно учесть граничные условия 2-го и 3-го рода:

ГУ 2-го рода:

ГУ 3-го рода:

С учетом всех преобразований получим:

где L_q и L_– части границы области S на которых задано ГУ 2-го и 3-го рода соответственно.

В том случае, если элементы трехузловые треугольные:

 (y_k x_j – y_j x_k – x_i (y_k – y_j)  y_i(x_k – x_j))/2.

Переходим к интегралам по элементам.

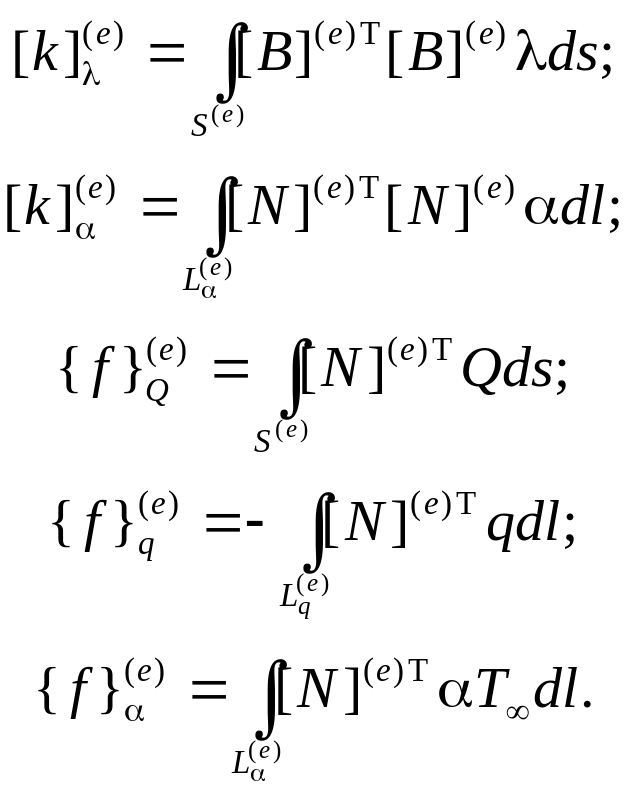
Примем допущение, что , Q, q,  постоянны в пределах элемента. Функции формы элементов запишем в локальных координатах и применим формулы для интегрирования (см. «локальная система координат двумерного симплекс-элемента»).

18