54. Фазовий простір і його властивості. Макро- і мікроканонічні стани речовини

Больцман і Максвел розробили статистичний метод дослідження фізичних процесів.На основі даного методу амер.фізик Гібсс розробив фізичні принципи, на яких базується вся класична і квантова фізика.

Розглянемо найпростішу термодинамічну систему – ідеальний газ.Якщовін займає деякий постійний об’єм V, то вона повністю буде характеризуватися тиском Р , з точки зору , статистичної фізики ідеальний газ є сукупністю великого числа частинок, які підлягають законам руху класичної фізики.Для характеристики цього стану можна скористатися двома способами:

• експериментально виміряти тиск Р і тоді стан газу буде характеризуватися одним параметром Р. Такий стан називається макроскопічним і за звичайних умов повітря можна вважати ідеальним газом;

• стан газу можна характеризувати як сукупність невзаємодійних матеріальних точок, тоді стан зручно зображати 6N – мірному просторі, де N- кількість частинок. Якщо положення одніє частинки характеризує координати x, y, z, то для характеристики усієї системи необхідно мати 3N координат.

Простір, за координатні осі якого взяті загальні координати називається конфігураційним .Взагалі координати позначаються .Це є уявний простір. В процесі руху узагальнуючі координати молекул будуть змінюватися, а отже і конфігураційний перехід однієї системи в іншу буде зображатися як переміщення матеріальних точок у такому конфігураційному просторі. Класична механіка стверджує , що для описання матеріальної точки необхідно задати і імпульси .Отже, щоб задати в даний момент часу стан N – чстинок необхідно задати 6N узагальнених координат і імпульсів. Такий стан називається мікроскопічним.

У ході переміщення молекул газ буде переходити з одного мікростану у інший, а цей перехід у конфігураційному просторі можна зобразити у вигляді деякої кривої названою фазовою траєкторією.Фазовий простір є уявним .Зобразити геометрично 6N – мірний простір неможливо, і лише для окремих випадків можна одержати конкретну геометричну криву, наприклад, у вигляді еліпса.

55.Розподіл молекул за швидкостями

Молекули газу перебувають у неперервному хаотичному русі, але газ вцілому не змінює своїх термодинамічних параметрів. Кожному рівноважному стану відповідає розподіл молекул за швидкостями, тобто такий розподіл, який встановлюється довільно і який фактично не змінюється. Швидкість молекул є випмдковою величиною і шукатимемо розподіл цієї випадкової величини. Його можна шукати вздовж деякогонапряму x, y, z, або за абсолютною величиною. Ці розподіли між собою пов’язані, оскільки швидкості можуть приймати довільні значення, отже, повинна існувати деяка неперервна функція розподілу f, яка не залежатиме від часу. Імовірність того, що молекули мають проекції швидкості на вісь Ох в інтервалі V_x V_x+dV_x визначаються співвідношеннями:

dW(V_x)=f(V_x²)dV_x

Аналогічно можна записати співвідношення для інших проекцій:

dW(V_y)=f(V_y²)dV_y

dW(V_z)=f(V_z²)dV_z

Імовірність того, що молекули одночасно матимуть 3 проекції V_x, V_y, V_z в інтервалі dV_x, dV_y, dV_z

dV_xdV_ydV_z=dW(dV_x, dV_y, dV_z)=f(V_x²)f(V_y²)f(V_z²)*dV_xdV_ydV_z. (23.1)

dW(dV_x, dV_y, dV_z)=f(V_x²)f(V_y²)f(V_z²)*dV_xdV_ydV_z (23.2)

f(V_x²)f(V_y²)f(V_z²)=f(V_x²+V_y²+V_z²)

Рівняння (23.2) задовільняє функція

f(V_x²)=A^1/3 , f(V_y²)=A^1/3 , f(V_z²)=A^1/3 (23.3)

або

f(V_x²+V_y²+V_z²)=A^1/3 (23.4)

α – деякий параметр, А – нормуючий множник, який з умови нормування можна визначити

.

Замість проекцій на вісь Ох можна взяти проекцію на будь-який напрямок і тоді:

f(V_x²)= (23.5)

Це і є розподіл за швидкостями, отриманий Максфелом і визначає імовірність того, що молекули мають швидкість у межах від V_e÷V_e+dV_e, але для аналізу молекулярного руху газів доцільно знати імовірність того, що молекула має той чи інший модуль швидкості не залежно від напряму руху, для цього потрібно перейти до сферичної системи координат і проробивши відповідні перетворення і одержимо наступний вираз для імовірності того, що молекула матиме певну швидкість, тобто

dW(V)= (23.6)

або з урахуванням коефіцієнта нормування функція розподілу

(23.7)

Це і є Максвелівський розподіл за швидкостями.

На практиці цікавлення розподілом не однієї молекули, а певною кількістю молекул dn(V) якщо система містить N молекул, то функція розподілу може бути записана як:

(23.8)

Якщо температура системи змінюється, то відповідно будуть змінюватися і швидкості молекул і розрахунки приводять до наступного виразу для розподілу молекул за швидкостями залежно від темперетури

(23.9)

Функцію розподілу (23.7) можна зобразити графічно.

Максимум розподілу вказує на те, що певна … молекул рухається з найбільш імовірною швидкістю, величина якої визначається як

.

Крім того швидкість характеризується середнім арифметичним V

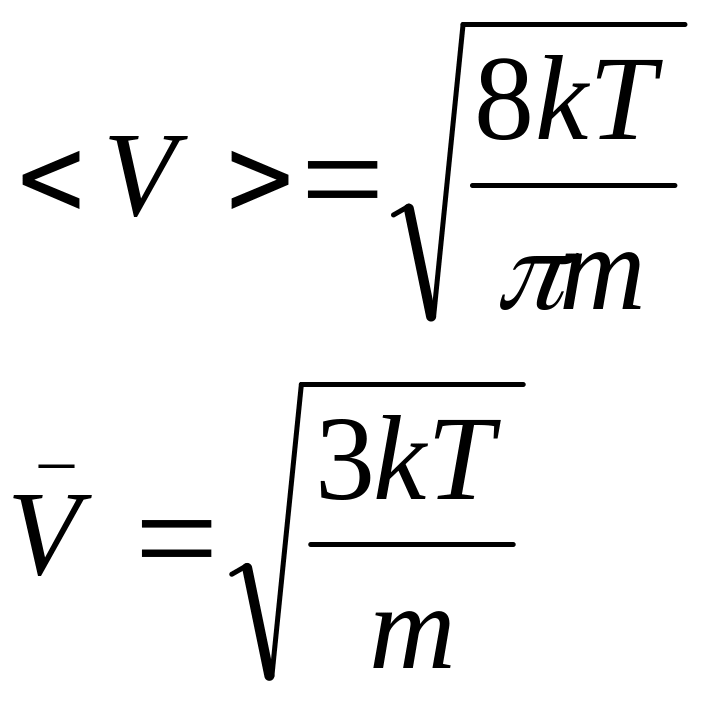
Квадратична швидкість визначає кінетичну енергію газу. Якщо ввести відносну швидкість

, то число молекул може бути визначене:

(23.10