63. Броунівський рух

Під ним розуміють хаотичний рух завислих мікроскопічних частинок в рідині або газі. Було відкрите Броуном, а пояснене Енштейном, як наслідок флуктуації числа і суми ударів, яких зазнає частинка з боку молекул газу або рідини.

Ці флуктуації пропорційні ,тому, якщо частинка велика, то з нею стикається дуже велике число n-молекул. А значить, флуктуації будуть малими і частинка не буде рухатись.

Завдяки наявності флуктуацій і здійснюється необоротнє переміщення частинок. Статистичні методи дозволяють розрахувати середнє квадратичне відхилення частинки від початкового положення як ф-ю часу.

Запишимо закон руху броунівської частинки у в язкому середовищі.

(1)

Домножимо (1) на

(2)

Для подальшого перетворення скористаємося

Отже (2) запишимо

(3)

Проінтегруємо (3) за t і розділимо почленно на t.

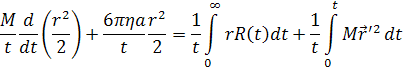
Отже, (3)

Введемо нову змінну Z=r²

(4)

Розв язок даного рівняння є сумою розв язку однорідного рівняння і частково неоднорідного.

Для випадку великих інтервалів часу цей розв язок перетвориться в 0.

(5)

Підставимо (5) у (4)

Знехтувавши малою М розв язок

Якщо ввести коефіцієнт , то

Тобто відхилення частинок пропорційне коефіцієнту дифузії та часу t.

64. Рівняння Фоккера-Планка

Явище броунівського руху послугувало поштовхом для створення теорії флуктуації.

Нехай є броунівська частинка радіуса R і масою m_0. На цю частинку буде діяти сила Стопса, але цього недостатньо для опису броунівського руху, тому Ланжеве увів деяку додаткову силу і це дозволило записати рівняння руху у виді

(1)

Сила не випливає з рівнянь гідродинаміки, а з являється лише як фактор наявності флуктуацій гідродинамічних ф-й.

Ця сила – ланджевенівське джерело і не може бути виведена.

Від рівняння (1) для випадкових ф-й можна перейти до рівняння розподілу швидкостей і координат f(r, v, t).

Вважатимемо, що число броунівських частинок є заданим, = N і є величиною постійною. Тобто

N(r, v, t)- фазова густина

Отже рівняння неперервності може бути записане

(2)

Ф-я розподілу пов язана із фазовою густиною співвіднош.

nf(r, v, t)=<N(r, v, t)> (3)

Тому (2) з урахуванням (3)

(4)

, то (4) запишимо

– фо-ла Фоккера-Планка

32