
- •15 Исследование фун-и на возрастание , убывание и экстремум.
- •16. Ряд Тейлора.
- •1.Разложение в ряд Тейлора ф-ции sin X.
- •2. Разложение в ряд Тейлора ф-ции cos X.
- •3. Разложение в ряд Маклорена ф-ции .
- •17 Первообразная и неопределенный интеграл.
- •Линейные свойства неопределенного интеграла.
- •Методы элементарных преобразований.
- •Интегрирование по частям.
- •Классы ф-ций, интегрируемых по частям:
- •Метод интегрирования подстановкой.
- •Метод замены переменной.
- •18.Определенный интеграл и его свойства. Интегрируемость непрерывной функции.
Метод замены переменной.
Т3:
Если ф-ция
имеет первообразную на
,
а ф-ция
![]() определена, дифференцируема на
и взаимнооднозначно отображает
определена, дифференцируема на
и взаимнооднозначно отображает
![]() ,
тогда ф-ция f(x)
интегрируема и имеет место формула:
,
тогда ф-ция f(x)
интегрируема и имеет место формула:
![]() (формула замены переменных).
(формула замены переменных).
Зам-ие1:
(Схема
применения).
Пусть дан
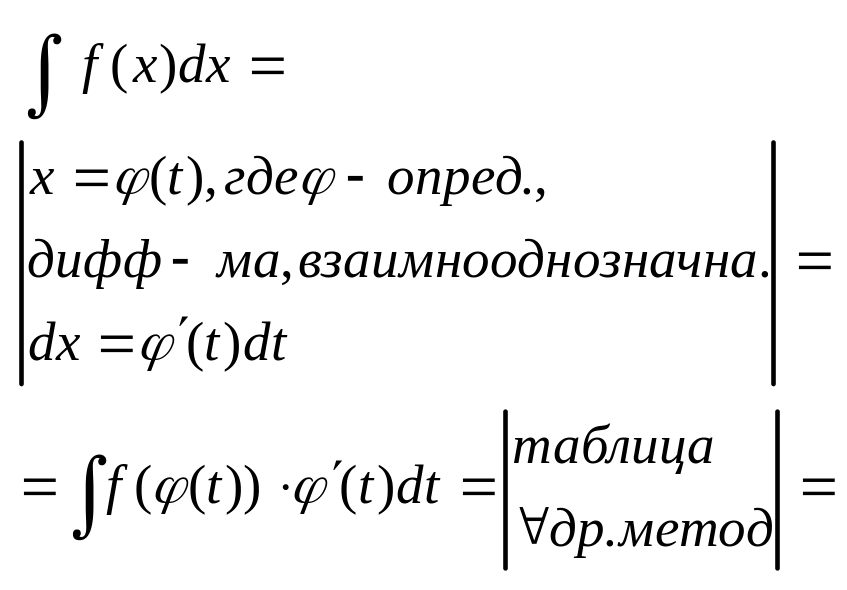
![]()
Зам-ие2: Ф–ция должна быть дифференцируемой и взаимнооднозначной. Это значит, что с одной стороны ф–ция должна быть непрерывной, с др. стороны (т.к взаимнооднозначна биективна инъективна строго монотонна) В качестве ф–ции можно брать любую удобную непрерывную на промежутке строго монотонную ф–цию.
Сл-ие1:
Если f(x)
имеет первообразную F(x),
тогда
![]() .
.
Сл-ие2:
Если f(x)
имеет первообразную F(x),
тогда
![]()
18.Определенный интеграл и его свойства. Интегрируемость непрерывной функции.
Пусть на ![]() определена и огр.
определена и огр. ![]() .
Произвольным образом разобьем
точками
.
Произвольным образом разобьем
точками ![]() .
На каждом
.
На каждом ![]() произвольным образом выберем точку
произвольным образом выберем точку
![]() .
Составим сумму, которую назовем
интегральной.
.
Составим сумму, которую назовем
интегральной. ![]() ,
где
,
где ![]() .
Будем увеличивать число точек деления
на части, добавляя новые к старым и
соблюдая условие при
.
Будем увеличивать число точек деления
на части, добавляя новые к старым и
соблюдая условие при ![]()
![]() .
Если не зависимо от способа разбиения
на части и выбора точки
.
Если не зависимо от способа разбиения
на части и выбора точки ![]()
![]() ,
то этот предел называют определенным
интегралом от f
на
и обозначают
,
то этот предел называют определенным
интегралом от f
на
и обозначают ![]()
Если интеграл ![]() существует, то функция f
называется интегрируемой на
.
существует, то функция f
называется интегрируемой на
.
Сумма Дарбу.
Пусть на
определена и огр.
.
Произвольным образом разобьем
точками
.
Если f
огр. на
,
то она и огр. на ![]() ,
т.е.
,
т.е. ![]() и
и ![]() .
Составим суммы
.
Составим суммы ![]() - верхняя сумма Дарбу,
- верхняя сумма Дарбу, ![]() - нижняя сумма Дарбу.
- нижняя сумма Дарбу.
![]() - площадь ступенчатой фигуры, расположенная
внутри крив. трапеции.
- площадь ступенчатой фигуры, расположенная
внутри крив. трапеции.
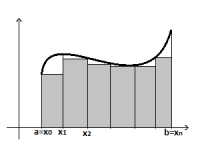
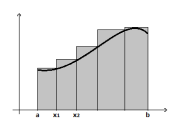
![]() -
площадь ступенчатой фигуры, внутри
которой расположена крив. трапеция.
-
площадь ступенчатой фигуры, внутри
которой расположена крив. трапеция.
Свойства сумм Дарбу:
При фиксированном способе разбиения сегмента на части
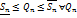 (за счет выбора точек
).
(за счет выбора точек
).
Доказательство:
Произвольно разобьем сегмент
на n
частей. Тогда ![]()
![]()
![]()
![]()
Сложим
все эти неравенства: ![]()
![]() .
.
При увеличении числа точек деления сегмента на части
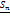 - возрастает,
- возрастает, 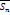 - убывает, т.е. (
)
– возрастающая последовательность,
(
)
– убывающая последовательность (при
- убывает, т.е. (
)
– возрастающая последовательность,
(
)
– убывающая последовательность (при
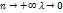 ).
).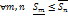
Из данного свойства
вытекает, что множество всех нижних
сумм Дарбу {![]() }
– огран. сверху; а {
}
– огран. снизу. След-но,
}
– огран. сверху; а {
}
– огран. снизу. След-но, ![]() - нижний интеграл Дарбу,
- нижний интеграл Дарбу, ![]() - верхний интеграл Дарбу.
- верхний интеграл Дарбу.
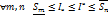
 При
фиксированном способе разбиения
сегмента
При
фиксированном способе разбиения
сегмента 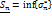 ,
,
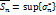 .
Эти множества получаются за счет
различного выбора точек
.
Эти множества получаются за счет
различного выбора точек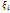 .
.
Необх и достат усл сущ-ния опр-ного интеграла (Т. Дарбу):
Пусть на
определена и огр.
.
Для того, чтобы она была интегрируема
на сегменте
необходимо и достаточно что ![]() .
.
Классы интегрированных функций:
Теорема 1: Если опр. и непрер. на сегменте , то она интегрируема на этом сегменте.
Теорема 2 (интегрируемость монотонной функции): Если монотонна на сегменте , то она интегрируема.
Теорема 3: Если функция ограниченная и имеет конечное число точек разрыва на сегменте , то она интегрируема.
Свойства определенного интеграла:
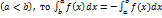
Если функции f и g интегрируемы на сегменте ,
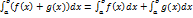 .
.Если f интегрируема на сегменте , то постоянный множитель можно выносить за знак интеграла
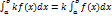 .
.Если f интегрируема на сегменте и точка
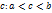 ,
то f
интегрируема на
,
то f
интегрируема на 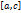 и
и 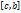 ,
причем
,
причем 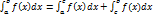 .
.Если интегрируема на
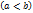 и
и 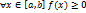 ,
то
,
то 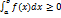 .
.
Док-во:
Строим последовательность (![]() ):
):
![]()
Перейдем к пределу
при
![]() (по свойству перехода к пределу в
неравенствах для последовательностей).
(по свойству перехода к пределу в
неравенствах для последовательностей).
Если и
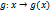 интегрируемы
на
и
интегрируемы
на
и 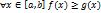 ,
то
,
то 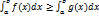 .
.Если интегрируема на и
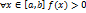 ,
то
,
то 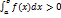 .
.Если и интегрируемы на и
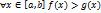 ,
то
,
то 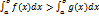 .
.Если интегрируема на и
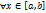 ;
;
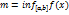 и
и 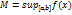 ,
то
,
то 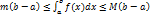 .
.Если интегрируема на , то
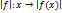 - интегрируема на
и
- интегрируема на
и 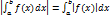 .
.
Теорема о среднем
1: Если
интегрируема на
,
то ![]() .
.
Доказательство:
1сл.
,
тогда по 9° ![]()
2 сл.
![]() ,
,
![]() .
.
3сл. a=b также выполняется.
Теорема о среднем
2: Если f
непрерывна на
,
то ![]() .
.
19.Опр-ный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
Пусть нам дана интегрируемая на .
По свойству
аддитивности определенного интеграла
(если f
интегрируема на ![]() ,т.е.
такая,что
,т.е.
такая,что ![]() ,
то f
– интегрируема на
и
причем
,
то f
– интегрируема на
и
причем ![]() ).
).
![]()
![]()
Если ![]() ,
то
,
то ![]() – определяем единственным образом.
Следовательно,
– определяем единственным образом.
Следовательно, ![]()
![]() - интеграл с переменным верхним пределом.
- интеграл с переменным верхним пределом.
Свойства интеграла с переменным верхним пределом.
Теорема 1. Непрерывность.
Если
интегрируема на
,
то функция ![]() непрерывна на
.
непрерывна на
.
Докажем это:
Возьмем произвольную
точку ![]() и докажем, что Ф непрерывна в точке
и докажем, что Ф непрерывна в точке ![]() .
.
Дадим приращение
![]()
![]()
 .
.
Inf
f(x)
![]() ,
но
,
но ![]() и
и ![]()
Следовательно, ![]() - не зависит ни от х0,
ни от
- не зависит ни от х0,
ни от ![]() .
.
![]() - ограниченная.
- ограниченная.
Вывод: б/м приращению аргумента соответствует б/м приращение функции Ф. Значит, функция Ф непрерывна в точке х0.
Теорема 2. Дифференцируемость.
интегрируема на [a,b]
непрерывна в точке
,
то функция
дифференцируема в точке
,
причем ![]() .
.
Следствие: если
непрерывна на [a,
b],
то
дифференцируема на [a,
b]
и ![]()
![]() ,
что означает, что Ф - одна из первообразных
для функции f.
,
что означает, что Ф - одна из первообразных
для функции f.
Формула Ньютона-Лейбница.
Теорема : Если f
– непрерывна на [a,
b],
то ![]() ,
где F
– одна из первообразных для f
на [a,
b].
,
где F
– одна из первообразных для f
на [a,
b].
F(x)=Ф(x)+С - свойство неопределенного интеграла.
![]()
Пусть x=a F(a)=0+C, т.е. С=F(a)
Пусть x=b
![]()
![]() .
.
