1.Разложение в ряд Тейлора ф-ции sin X.

Возьмем , покажем, что sin x разложима на нем в ряд Тейлора.

1.

Рассмотрим разложение с центром в т. . Такие ряды наз. ряды Маклорена.

2. .

Выполняются все условия Т.4 разложима в ряд Тейлора и в ряд Маклорена.

Вычислим

Все повторяется через 4. Причем все производные четного порядка равны нулю.

Ряд Маклорена для имеет вид:

для

Радиус сходимости этого ряда . Значит, ряд равномерно сходится на любом отрезке . Значит, его можно почленно дифференцировать на любом интервале .

.

2. Разложение в ряд Тейлора ф-ции cos X.

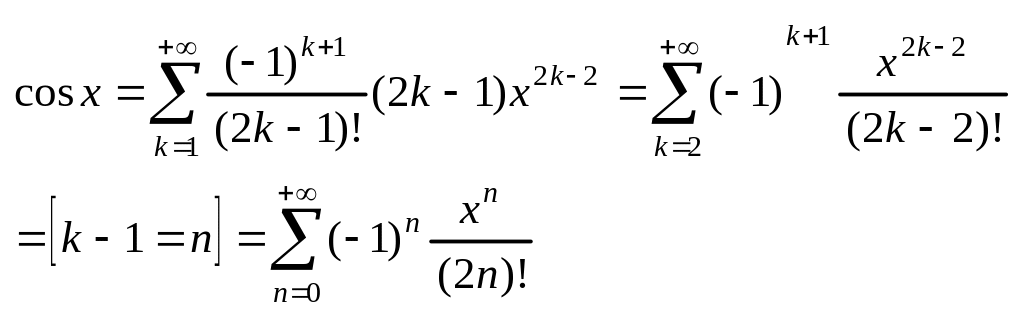
для сходится равномерно.

Для ф-ции можно получить разложение в ряд Маклорена, используя Т4:

Выполняются все условия Т.4 разложима в ряд Тейлора и в ряд Маклорена.

Вычислим

Все повторяется через 4. Причем все производные нечетного порядка равны нулю.

Ряд Маклорена для имеет вид:

для

3. Разложение в ряд Маклорена ф-ции .

Зам-ие: При получаем формулу для приближенного вычисления числа е, .

4.Разложение в ряд Маклорена ф-ции . для сходится равномерно на

- биномиальные коэффициенты, отличные от нуля.

17 Первообразная и неопределенный интеграл.

Задачи вычисления первообразных ф-ций возникают из задач о восстановлении пути, пройденным телом за промежуток времени по известной скорости (физич. интерпретация). Восстановление ф-ции по ее производной (математ. интерпретация).

Опр.1: Ф- ция F(x) назыв. первообразной для ф-ции f(x) на мн-ве D, если .

Опр.2: Ф- ция F(x) явл- ся первообразной для ф – ции f(x) на D, если:

1. F(x) дифференц – ма на D

2. 

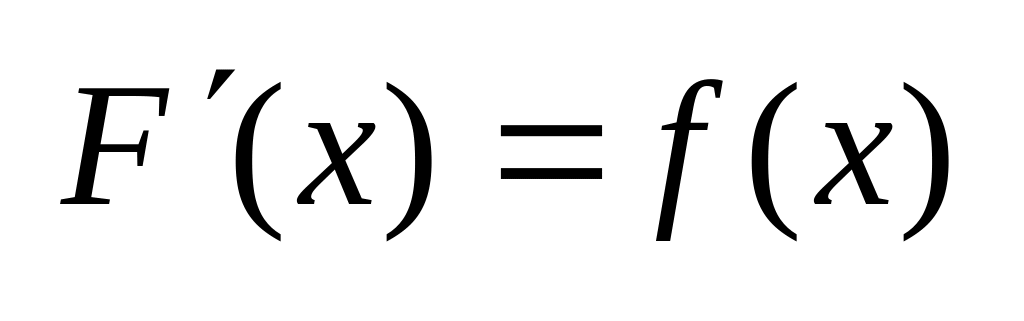
Возникают след. вопросы:

1. у всякой ли ф-ции существует первообразная;

2. если первообразная существует, то единственна она или нет;

3. если первообразная не единственна, то как найти мн–во всех первообразных.

Т1: Если ф-ция , то у нее всюду на этом промежутке ( ) существует первообразная ф–ция

Т2: Пусть F(x) – первообразная для ф–ции f(x) на . Тогда для того, чтобы ф–ция Ф(x) являлась первообразной для ф–ции f(x) на необходимо и дост–но Ф(x)= F(x)+ C.

Зам-ие1: Если ф–ция f(x) имеет на промежутке первообразную, то любая другая первообразная отличается от исходной всего лишь на константу.

Зам-ие2: О существовании первообразных говорим только на промежутке.

Опр.3: Мн–во всех первообразных данной ф–ции f(x) назыв. неопределенным интегралом, обозначается . В расчетах:

Терминология: Операцию нахождения первообразных назыв. интегрированием. Ф–ция, у которой существует первообразная, наз. интегрируемой.

Зам-ие: Если ф–ция не имеет первообразной на промежутке , то ее неопред. интеграл явл. пустое мн–во.

f(x)dx – подинтегральное выражение

f(x) – подинтегральная ф-ция .

Свойства неопределенного интегрла.

Св–во1: Пусть интегрируема на , тогда производная от ее неопред. интеграла равна подинтегральной ф–ции, т.е. .

Св–во2: Пусть интегрируема на , тогда дифференциал от неопред. интеграла равен подинтегральному выражению, т.е. .

Св–во3: Пусть дифференцируема на , тогда ф–ция интегрируема на промежутке и имеет место равенство:

Св–во4: Если ф–ция дифференцируема на , то интеграл .