14. Основные теоремы дифференциального исчисления: Ферма, Роля, Лагранжа, Коши.

Опр-е1. Будем говорить, что ф-ция достигает на промежутке наибольшего значения, если

Опр-е2. Говорят, что ф-ция достигает на промежутке наименьшего значения, если

Обозначение наиб. значение на промежутке; наим. значение на промежутке.

Теорема Ферма

Если ф-ция определена на промежутке и непрерывна на этом промежутке, достигает в его внутренней точке наибольшего и наименьшего значения ,

, то тогда не существует в или .

Зам-е1: Если у ф-ции удовлетворяющей теореме Ферма производная в точке, в которой ф-ция принимает наиб. или наим. значение, обращается в ноль, то значит тангенс угла наклона касательной в этой точке равен нулю и значит в этой точке касательная параллельна оси абсцисс.

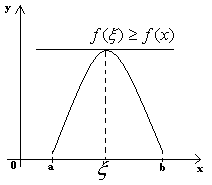
Зам-е2: Условие о том, что точка внутренняя для промежутка явл. существенным.

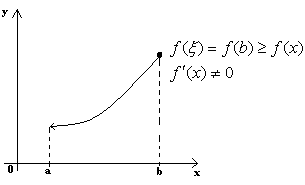
Если ф-ция достигает наиб. или наим. значения на конце промежутка, то значение производной в этой точке может и не быть равным нулю.

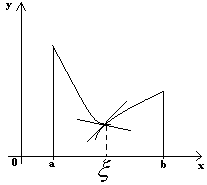
Зам-е3: Точка внутренняя, а не существует.

, наим. значение.

Зам-е4: Теорема Ферма явл. необходимым условием существования наиб. или наим. значения ф-ции на промежутке.

Из не следует что наиб. или наим. значение.

Пример: , но не явл. ни наиб. ни наим. значением.

Опр-е3: Если в некоторой точке внутренней для промежутка производная ф-ции обращается в ноль или не существует, то точка называется критической точкой ф-ции .

Опр-е4: Если в некоторой точке внутренней для промежутка производная ф-ции обращается в ноль, то точка называется стационарной.

Теорема Роля

Пусть 1). ф-ция определена на отрезке и непрерывна на нем

2). и 3).

Тогда .

Зам-е1: Если ф-ция на отрезке удовлетворяет всем условиям теоремы Роля, то секущая к графику ф-ции, проведенная через точки и параллельна оси абсцисс.

Теорема Роля означает, что внутри отрезка всегда найдется хотя бы одна

точка, в которой касательная к графику ф-ции будет параллельна секущей и значит параллельна оси абсцисс; таких точек может быть и 2, и 3 и

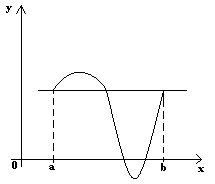
Зам-е2: Если ф-ция на отрезке удовлетворяет всем условиям теоремы Роля, то значит между двумя нулями ф-ции всегда найдется хотя бы один ноль производной.

Теорема Лагранжа

Если ф-ция определена на отрезке и непрерывна на нем (отрезок невырожденный, т.е. ) и

, то

Тогда .

Док-во: Построим вспомогательную ф-цию , где Подберем эту константу т.о. чтобы ф-ция удовлетворяла теореме Роля

1). (как сумма двух непрерывных ф-ций)

2). (производная суммы)

3). , т.е. выполняется условие ; тогда

Значит удовлетворяет всем условиям теоремы Роля, и значит

Вычислим производную ф-ции

т.о. доказали.

Эта формула конечных приращений Лагранжа

Зам-е:

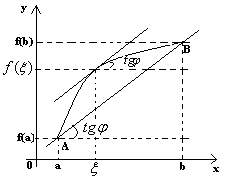
проведем секущую АВ через точки и (ф-ция удовлетворяет теореме Лагранжа) . Теорема Л. говорит о том, что внутри интервала АВ найдется точка такая что касательная проведенная к графику ф-ции в т. будет параллельна секущея АВ.

Сл-е1: Для того чтобы ф-ция была на промежутке постоянной необ. и дост. чтобы всюду внутри этого промежутка производная равнялась нулю.

Сл-е2: Для того, чтобы ф-ции и определенные и дифференцирован-ные была на различались на этом промежутке на константу необ. и дост. чтобы их производные были равны между собой всюду на этом промежутке.

Теорема Коши

Пусть 1). ф-ции и определена и непрерывны на и непрерывна на нем

2).

3).

Тогда

.

15 Исследование фун-и на возрастание , убывание и экстремум.

Опр1. Внутр тотчка х₀ принадл (a,b) наз точкой локального минимума если сущ U_δ(x₀) т. ч. Для люб х принадл U_δ(x₀)\{x₀} f(x)>f(x₀).

Опр2. Внутр тотчка х₀ принадл (a,b) наз точкой локального максимума если сущ U_δ(x₀) т. ч. Для люб х принадл U_δ(x₀)\{x₀} f(x)<f(x₀).

Опр3. Точки локального минимума и максимума наз точки локального экстремума.

Опр4. Значение ф-и в т лок миним наз локальным минимумом.

Опр5. Значение ф-и в т лок максимума наз локальным максимумом ф-и.

Теорема (Условие постоянства ф-и на промежутке )

Пусть ф-я f опр и непрер на <a,b> и для люб х из <a,b> сущ f’(x) из R тогда для того чтобы f(x)=const↔ f’(x)=0.

Док-во.

1)необх следует из табл производных.

2)дост Имеем право применить формулу конечных приращений. По теор Лагранжа

f(x)-f(x₀)=f’(ξ)(x-x₀)

f’(ξ)=0→ f(x)-f(x₀)=0→для люб x, x₀ из <a,b> f(x)=f(x₀)→ f(x)=сonst на <a,b>

Теорема 2(условие монотонности ф-и на промежутке)

Пусть ф-я f опр и непрер на <a,b> и для люб х из <a,b> сущ f’(x) из R тогда для того чтобы f монотонно ↑(↓) необх и дост для люб х из <a,b> f’(x)≥0 (f’(x)≤0)

Док-во.

1)необх. f ↑→ f’(x)≥0

Т.к f ↑, то для люб x<x₀ из <a,b> f(x₁)≤f(x₂). Т. к. сущ. f’(x) из R→ сущ lim ∆f(x,∆x)/ ∆х в R с чертой при ∆х→0 → сущ ∆f(x,∆x)

х принадлежит <a,b> и х+∆x принадлежит <a,b> . возьмем отношение ∆f(x,∆x)/ ∆х=f(x+∆x)-f(x)/ ∆х

возможны 2 случая

1) ∆х≥0 х+∆х≥х f’(x)=lim ∆f/∆х≥0

2) ∆х≤0 х+∆х≤х f(x+∆x)-f(x)≤0 f’(x)=lim ∆f/∆х≥0

Т. о. получили, что для люб х из <a,b> f’(x)≥0

2) достат

Т.к. сущ. f’(x) из R и f непрер , то удовлетвор всем услов теор Лагранжа, т.е. f(x₂)-f(x₁)= f’(ξ)(x₂-x₁), где для люб x₁ x₂ из <a,b> ξ принадл (x₁ , x₂ ) f принадл [x₁ , x₂ ]

Возможны 2 случая

А) x₁ <x₂, тогда f’(ξ)≥0 x₂ - x₁>0 , тогда f(x₂ )-f(x₁ ) ≥0. т.е. x₁ <x₂→ f(x₁ )≤ f(x₂ )

Б) x₂ <x₁, тогда f’(ξ)≥0 x₂ - x₁<0 , тогда f(x₂ )-f(x₁ ) ≤0. т.е. x₂ <x₁→ f(x₂ )≤ f(x₁ ) → f ↑.

Для f ↓ аналогично.

Теорема 3

Пусть 1) f непрерна <a,b>

2) для люб х принадл <a,b> сущ f’(x) из R c чертой, тогда для того чтобы f ↑↑ необх и дост

а) для люб х из (a,b) f’(х)≥0

б) мн-во нулей первой производной не заполняло сплошь ни одного промежутка, сост часть <a,b>.

Теорема 1 (необх условие экстремума).

Пусть f 1) определена на <a,b> → R

2) пусть сущ х₀ принадл (a,b) в котором ф-я испыт экстремум, тогда f’(x₀)=0 либо f’(x₀) не сущ в R с чертой.

Теорема 2 (первое дост условие )

Пусть 1)f <a,b> → R

2)сущ х₀ принадл <a,b> f’(x₀)=0

3) непрер и дифф-ма на U_δ(x₀)\{x₀} , тогда а) если при переходе через x₀ производная меняет знак с + на -, x₀ – локального максимума.

Б) с – на + x₀ – локального минимума.

В) елли производная не меняет знак, то x₀не явл т. эстремума.

Док-во.

А) пусть производная при переходе меняет знак с + на - . Рассмотрим U_δ^-(x₀). Для люб х принадл U_δ^-(x₀) сущ f’(x)= lim f(x)-f(x₀)/x-x₀>0.

Возьмем произвольную точку х₁ є U_δ^-(x₀) [x₁x₀] на этом отрезке проходят все условия теоремы Лагранжа f(x₁)-f(x₀)=f’(ξ)(x₁-x₀) ξє[x₁x₀]

x₁ -x₀<0 f’(ξ)>0 → f(x₁)-f(x₀)<0→ f(x₁)<f(x₀)

для любого х₁ є U_δ^-(x₀) [x₀x₂] на этом отрезке проходят все условия теоремы Лагранжа f(x₁)-

f(x₀)-f(x₂)= f’(ξ)(x₀-x₂)>0→ f(x₀)>f(x₂)

в силу произвольности х₁ х₂ получаем: Для люб х принадл U_δ(x₀)\{x₀} f(x)<f(x₀).→ x₀ т. лок. максимума.

Б) Аналогично

В) для определенности предположим, что + x₀ +

для любого х₁ є U_δ^-(x₀) f(x₁)-f(x₀)=f’(ξ)(x₁-x₀)<0→ f(x₁)<f(x₀).

для любого х₂ є U_δ⁺(x₀) f(x₂)-f(x₀)=f’(ξ)(x₂-x₀)>0→ f(x₂)>f(x₀), тогда в U_δ(x₀) f(x₁)<f(x₀)< f(x₂), ф-я мон возрастает и экстремума не испытыват.

Для -x₀- аналогично.

Теорема 3 (второе дост условие )

Пусть 1)f <a,b> → R

2)сущ х₀ принадл <a,b> явл критич точкой.

3) непрер и дифф-ма на U_δ(x₀)\{x₀}

4) сущ f’’(x₀)≠0 , тогда

а) f’’(x₀) >0→ x₀ точка лок минимума .

Б) f’’(x₀) <0→ x₀ точка лок максимума.

В) f’’(x₀) =0, то вопрос отркрыт.

Теорема 4 (третье дост условие ).

Пусть 1)f <a,b> → R

2) сущ f^(n-1)(x₀)=0

3) сущ fⁿ(x₀)≠0

Тогда, если n чет , то а) fⁿ(x₀)>0 → x₀ точка лок минимума

б) fⁿ(x₀)<0 → x₀ точка лок максимума.

Если n нечет , то экстремума нет.

Наибольшее и наименьшее значение ф-и на промежутке

Пусть дана ф-я f [a,b] → R непрер и дифф-ма на [a,b] всюду за исключением конечного числа точек.

Т.к непрер, то по 2 Т Вейерштрасса , она достигает своих наибольших и наименьших значений.

Рассмотрим 2 ситуации

1. наибольшее значение достигается на одном из концов этого отрезка

2. наибольшее значении достигается во внутренней точке х₀.

Раз ф-я достигает наиб знач во внур точке, то по Т.Ферма сущ f’(x₀)=0 или не сущ в R c чертой. подозрительный на глобальный максиму могут быть концы отрезка и точки подозрительные на локальный экстремум.