11. Гармонические колебания и их характеристики. Смещение, скорость и ускорение при гармоническом колебательном движении.

Колебание – это движение или процесс, обладающий той или иной повторяемостью от времени.

В физике выделяют 3 вида колебаний:

1. механические (звук, вибрация);

2. электромагнитные (свет, радиоволны);

3. электромеханические (механические и электромагнитные вместе);

Различают также колебания:

Свободные – это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие): колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Вынужденные – колебания, протекающие в системе под влиянием внешнего периодического воздействия (листья на деревьях, поднятие и опускание руки). При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.

Автоколебания – колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от свободных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.

Гармонические колебания – колебания, совершаемые (изменяемые) по закону синуса (кисинуса).

X=Asin( t+α)

X=Acos( t+α), где X – смещение, t+α – фаза, α – начальная фаза, A – амплитуда.

Период колебания Т – это время, за которое фаза получает приращение 2π.

[ (t+Т)+α] = t+α+2π

T=

v= = =-A

a= = = = -A cos(

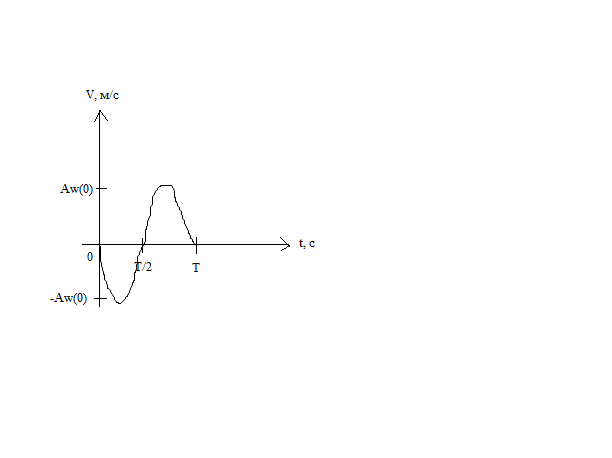
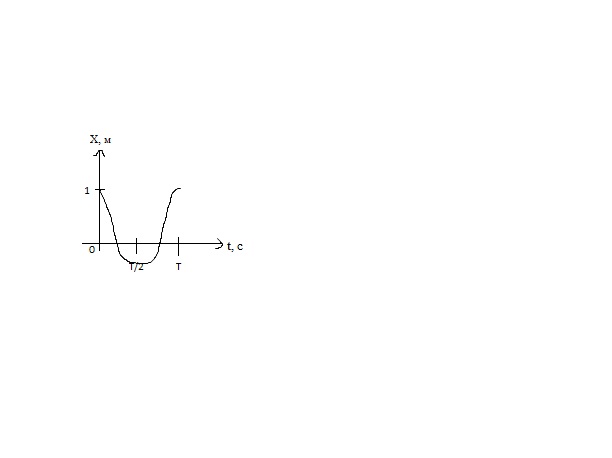
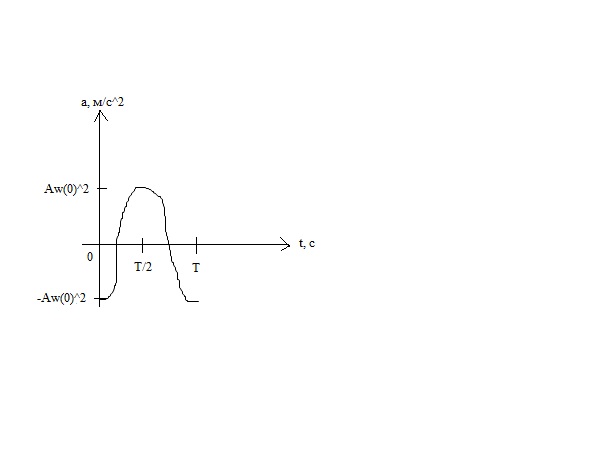
12. Дифференциальное уравнение гармонических колебаний. Пружинный, математический и физический маятники

Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеб­лющаяся величина изменяется со временем по закону синуса (косинуса): , , где -смещение,А - амплитуда колебания,₀ —круговая (циклическая) частота, —начальная фаза колебания в мо­мент времени t=0, — фаза колебания в момент времени t.

Запишем вторую производную по времени от гармонически колеблющей­ся величины x: (2).

Если сопоставить уравнения (1) и (2), то можно записать дифференциальное уравнение гармонических колебаний .Решением этого уравнения является функция . Константы и определяются начальными условиями. Все уравнения типа решаются по одному и тому же закону - круговая частота. Если какая–то сила действует на на колеблющее тело, то , где - жесткость (волновое число). Следовательно, сила пропорциональна смещению со знаком «-». Силы такого типа называется квазиупругими.

Пружинный, физический и математический маятники

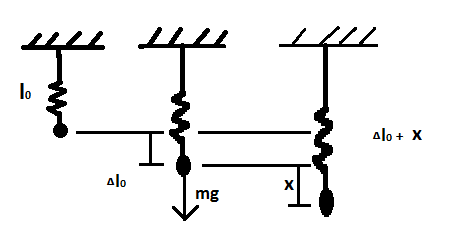1. П ружинный маятник — это груз массой m, подвешенный на упругой пружине и совершающий гармонические колебания под действием упругой силы F= –kx, где k —жесткость пружины.

Пружинка длиной . Если на кончик пружинки прикреплен шарик массой m, то пружинка растянется под действием силы тяжести . Возникает уравновешенная сила .(3) Сместим шарик еще ниже на x. Смещение станет .

На шарик действует сила . С учетом (3) получаем (квазиупругая сила).

Если сообщить маятнику смещение , то начнутся колебания пружины: по 2-му закону Ньютона . , где

2. 

   O

   Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеб­лющаяся под действием силы тяжести.

Если оттолкнуть нить, то возникнет вращающий момент: .

. Вращающий момент стремится вернуть маятник в положение равновесия. Следовательно, вращающий момент носит характер квазеупругой силы. Тогда . Если -малый угол, то . Тогда, учитывая, что у нас вращательное движение, т.е. момент силы равен моменту энерции ускорения: . или , а , а так как

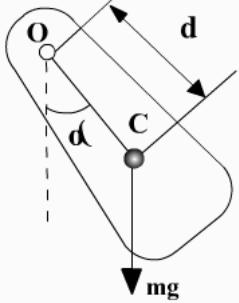3. Ф изический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела.

- вращающий момент, . Следовательно, вращающий момент стремится вернуть маятник в положение равновесия. Вращающий момент носит характер квазеупругой силы. Тогда , , , . (приведенная). , , где .