5. Осевой момент инерции мт и системы мт. Теорема Штейнера.

(1) (2)Рисунок!!!!

Если взять производную от момента импульса какой-то частицы массой ∆m,то получаем

(3)

–проекция момента импульса на ось t

Угол α – угол между векторами . α=

- как угол между взаимными перпен-ми сторонами

(4)

Полная проекция :

(5) – момент инерции

Величина = сумме произведения элементов масс на квадрат расстояний их до некоторой оси z,проходящей через это тело наз. моментом инерции тела относительно этой оси.

Мера инертности при поступательном движении – масса, при вращательном движении - .

– аналог m при вращательном движении.

Т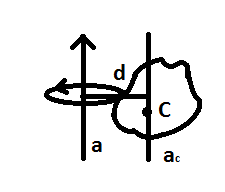 еорема ШТЕЙНЕРА. Момент инерции тела относительно произвольной выбранной оси a= сумме моментов инерции тела относительно параллельной ей оси ,проходящей через центр масс С-тела и произведения массы тела на квадрат расстояния между осями.

(6)

5. Основное уравнение динамики вращательного движения.

(1) (2)

Если взять производную от момента импульса какой-то частицы массой ∆m,то получаем

(3)- осн.закон динамики вращательного движения.

–скорость изменения момента импульса по t=суммарному моменту сил действующих на частицу.

– производная по t от момента импульса относительно оси z равна моменту силы относительно этой же оси, которая действует на частицы.

, где М_i– главный момент внешних сил, действующих на систему материальных точек.

5. Законы изменения и сохранения моментов импульса.

-скорость изменения момента импульса со временем равна суммарному моменту сил действующих на частицы.

Для проекции справедливо:

Производная по времени от момента импульса относительно оси z равна моменту силы относительно этой же оси, которая действует на частицы:

Закон изменения момента импульса:Производная по времени момента импульса механической системы равна сумме моментов внешних сил или главному моменту внешних сил.

, где -главный момент внешних сил, действующих на материальное тело.

Закон сохранения момента импульса: момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее равен 0.

Для консервативных систем (нет внешнего воздействия) , следовательно момент импульса , значит -const.

9.Работа силы. Мощность.

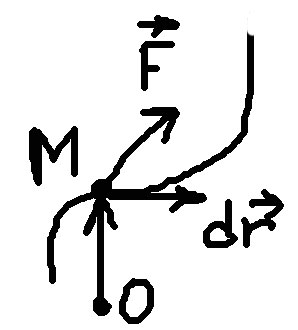
Если материальное тело движется по произвольной траектории (рис. 1) материальное тело характеризуется радиус-вектором относительно т. О. На нее действует сила F.

Элементарной работой силы на малом перемещении т. М приложенной силы называется скалярное произведение на , то есть:

=( )

=Fdrcosα

=( ) =( )=( )dt

, если:

1. dr=0;

2. ;

3. α< , >0;

4. α> , <0;

Мощностью N силы называется отношение элементарной работы , совершаемой этой силой F за малый промежуток времени к его длительности.

скорость перемещения точки перемещения силы.

10. Кинетическая и потенциальная энергия. Закон сохранения механической энергии.

Механика включает 2 вида энергии:

1.Кинетической энергией наз-ся энергия механического движения системы.

dW_k=( ,dr)=( , )dt

dt=d =>dW_k=(d ,v)= (d , )

( ,d )= d( , )= d( ²)= d

dW_k=( ,d )= d( ²)

W_k= ²= mv²

Для малого элемента массой dm кинет.энергия dWˈ_k, если этот элемент стоит на расстоянии r от оси вращения. dW_k= vdm= w²R²dm

W`_k= w²R²dm= w² K²dm= w²

W_k=W_k^пост+W_k^вращ= mv²+ w²

2.Кроме кинетич.энергии тело может обладать потенциальной энергией.

Если F(x,y,z) одинаковая во всех точках и направлениях;F(t)=const; то такая сила наз-ся консервативной.

В консервативных системах (действ. только внутри системы) работа действующих сил зависит от начального и конечного положения

A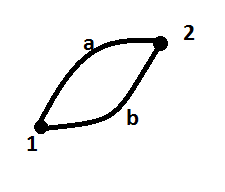 _1a2=A_1b2=A_{12 ,}

A_1a2b1=A_1a2+A_2b1=A_1a2-A_1b2=0

A= dr – уравнение циркуляции в-ра F вдоль замкн. Круга L=0.

Теорема о циркуляции: циркуляция вектора вдоль замкнутого круга L=0

А₁₂=W_n(1)-W_n(2)=-[ W_n(2)-W_n(1)]

Потенциальная энергия – величина, численно равная работе, кот-ю совершают все действующие на систему потенц. cилы при переводе этой системы из рассматриваемого состояния в состояние соответствующее его нулевой конфигурации.

Элементарная работа A=-dW_n => что потенциальной энергией механич.систназ-ся величина, численно = работе, которую совершают все действующие на систему потенциальные силы при переводе сист.из рассматриваемого состояния в состояние, соответствующее нулевой конфигурации.

Если рассматривать сист.из n материальных точек, то ее сист. кинетич.энергии W_k= (mv₁²+ _iw²)

Изменение кинетич.энергии при малом перемещении сист.=работе, совершенной этой системой.

dW_k= Для МТ

dW_k=

A_i= A_i^конс+ A_i^неконс

dW_k= +

A_i^неконс= A^неконс

A_i^конс= A^конс=-dW_n

З-н изменения энергии: dW_k=-dW_n+ A^неконс =>dW_k+dW_n= A^неконс

Изменение механич.энергии системы равно алгебраич. сумме работ всех неконс.сил, действующих на сист. Если сист. находится только в поле консервативных сил, то A^неконс =0 =>dW=0

З-н сохр.энергии: dW_k+dW_n=d(W_k+W_n)=0

W_k+W_n=const

Закон сохранения энергии:

Полная механическая энергия сист.мат.точек, находящаяся под действием только консервативных сил, остается постоянной.