43.Единство волновых и корпускулярных свойств элм излучения. Гипотеза де-Бройля. Опытное обоснование корпускулярно-волнового дуализма веществ. Опыты Дэвиссона и Джермера.

1. Если волне можно приписать св-ва частиц, то почему частицам нельзя приписать св-ва волны? ( предположение Луи Дембройля). Каждая частица, как и фотон света, обладает импульсом, а потому хар-ся некот-ой длины волны .

(2)

h-постоянная Планка

h 6,6* Дж/с

m 0.2 кг

v 15 м/с

разность потенциала

e Кл

eU ,

гипотеза де-бройля: предположим, если частица обладает корпускулярны св-м то она будет обладать волновым.

2) Направим пучок электронов на монокристалл Дикенса

Ц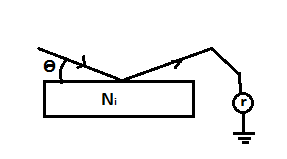 илиндр Фарадея

2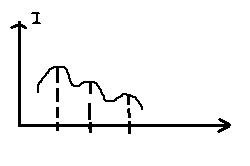 dsin

n

Корпускулярно-волновой дуализм сочетание свойств волны и частиц.

44.Волновая функция, её статистический смысл. Соотношение неопределённостей Гейзенберга.

Для описания распределения вероятности нахождения частицы в данный момент времени t в некоторой точке системы координат (x, y, z) вводится волновая функция ϕ. Она определяется из того, что вероятность dω нахождения частицы в элементарном объеме dv пропорциональна квадрату модуля волновой функции ψ.

– определяет интенсивность волн Деброиля

Свойства волн де-Бройля:

1. Это не электромагнитные волны

2. Имеют специфическую квантовую природу, не имеющую аналогии с волнами классической физики

Для этих волн справедливо, что тройной интеграл по всему пространству

Это значит, что частица пребывает где-либо в пространстве и это достоверное событие, так как вероятность равна 1.

В 1927 году Гейзенберг сформулировал принцип неопределенности: если ∆x – неопределенность в определении координаты x, а – неопределенность в определении импульса частицы x, то их произведение не может превосходить ћ (постоянную Планка).

Электрон не может обладать фиксируемой длиной волны (или частотой), значит работает правило

И наоборот, если задать интервал ( , то электрон можно обнаружить в области:

Соотношение неопределенности Гейзенберга применимо для энергии частицы в определенный момент t, т.е.

Если мы хотим точно определить энергию частицы, то она не может быть определена с точностью

45. Общее и стационарное уравнения Шредингера, их применение для решения физических задач

В класич. физике использ. уравнение Ньютона. Основное динамическое уравнение нерелятивистской квантовой механики было предложено австрийским физиком Э. Шрёдингером в 1926 г. Оно описывает изменение во времени состояния квантового объекта, характеризуемого волновой функцией.

Если известна волновая функция Ψ(t) в начальный момент времени, то, решая уравнение Шрёдингера, можно найти Ψ(t) в любой последующий момент времени t.

Запишем уравнение Шрёдингера для частицы массой m, в поле силы, порождаемой потенциалом U(x, y, z, t):

-временное уравнение Шредингера.

i – мнимая единица, Ψ(x, y, z, t) – искомая волновая функция. Скорость частичек много меньше скорости света( ).

Если потенциальная энергия U не зависит от времени, то Ψ(x, y, z, t)= Ψ(x, y, z).Тогда уравнение Шредингера можно переписать след. образом:

U(x, y, z) , U(x, y, z, t)

, U-смысл потенциальной энергии,

, ( )=0-стационарное уравнение Шредингера.

Функции , которая удовлетв.стационармному уравнению наз.собственными функциями, а значения W, которые удовлетвор. стационарному ур-ю назыв. собственными значениями.

, ,

это есть вероятность нахождения частицы в момент времени t в квантовом состоянии n в точке пространства и эта вероятностная интерпретация есть один из главных постулатов в квантовой механике.

Уравнение Шредингера используется для описания движения свободной частицы, для описания поведения частицы в потенциальной яме для описания туннелирования частицы через потенциальный барьер.