7. Определения: плотность (дифференциальная), распределения (интегральная).

Интегральная функция распределения

Функцией распределения называют функцию F(x), определяющую

вероятность того, что случайная величина Х в результате испытания

примет значение, меньшее х.

F(x) = P(X < x) .

Функцию распределения также называют интегральной функцией.

Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

            Плотность распределения также называют дифференциальной функцией.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

8. Математическое ожидание и дисперсия случайной величины (дискретный и непрерывный случаи).

Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения.

Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины

Пусть задано вероятностное пространство и определённая на нём случайная величина . То есть, по определению,  — измеримая функция. Если существует интеграл Лебега от по пространству , то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается или .

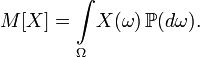
• Если 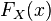 — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:

.

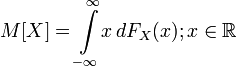Математическое ожидание абсолютно непрерывного распределения

• Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью 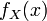, равно

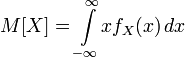
Дисперсия случайной величины

Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается

В статистике часто употребляется обозначение или . Квадратный корень из дисперсии, равный , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом.

где символ обозначает математическое ожидание

9. Основные дискретные распределения: биномиальные, распределение Пуассона.

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из   независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна  .

Функция распределения биномиального распределения может быть записана в виде суммы:

,

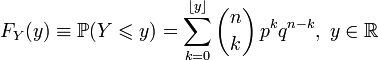где   обозначает наибольшее целое, не превосходящее число  , или в виде неполной бета-функции:

________________________________________________________.

Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение [править]

Выберем фиксированное число   и определим дискретное распределение, задаваемое следующей функцией вероятности:

,

где

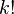•  обозначает факториал числа  ,

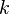•  — основание натурального логарифма.

Тот факт, что случайная величина   имеет распределение Пуассона с параметром  , записывается:  .