Равномерное движение жидкости в каналах.

Равномерное движение жидкости в открытых руслах происходит под действием силы тяжести и наличии геометрического уклона.

Равномерное движение происходит:

1. Q(расход) не изменяется.

2. Уклон так же постоянен

3. Площадь поперечного сечения постоянна

4. Шероховатость дна и стенок постоянна

5. Отсутствуют местные сопротивления

Такое движение может наблюдаться лишь в искусственных лотках, кюветах. Рассмотрим жидкость движущуюся равномерно:

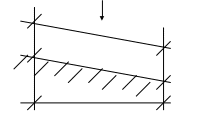Pa

h

h

z₁ z₂

0. 0

z₁ – z₂ = h_1-2 | :l

уклон дна гидравлический уклон

Уклон дна и гидравлический уклон совпадают по свободной поверхности параллельно дну и равны пьезометрическому уклону J.

J = i_д = i, где

i_д –уклон дна

i – гидравлический уклон

J – пьезометрический уклон

R=

Гидравлический радиус рравен отношению живого сечения к смоченному периметру.

-уравнение Шези.

С – коэффициент Шези

R – гидравлический радиус.

Часто =W – модуль скорости ( задается в справочниках)

Q=ωυ=ω =ωW =k

ωW=k

k – модуль расхода ( расходная характеристика)

Определим коэффициент Шези в круглой трубе, для этого приравняем формулу Шези и формулу Дарси.

R = для круглой трубы

Для каналов в которых жидкость движется в турбулентном режиме применяется формула Павловского:

(*)

n – шероховатость канала

R – гидравлический радиус

y – показатель степени

Частным случаем (*) является формула Маннинга:

Q = ω = ω = ω

Q = , где z = y+1/2

1. Симметричные каналы:

1.

h

dφ

b

ctgφ=m

R =

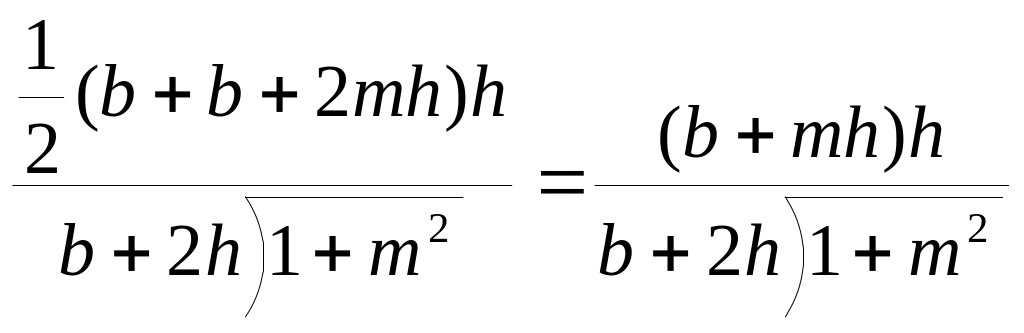
2.

h ctgφ=0, следовательно φ=90⁰

b

3.

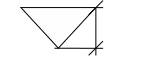
b h b=0

4 .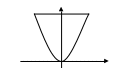

y

0. x

x²=2py

2. Несимметричные каналы:

3. Естественные каналы:

4. Каналы составного профиля:

5.Каналы замкнутого профиля:

Гидравлически наивыгоднейшее сечение канала.

При проектировании каналов встает вопрос о выборе его формы и размеров. Предпочтительней выбирать такую форму и размеры, при которых при заданной площади поперечного сечения, шероховатости стенок и дна, гидравлическом уклоне, расход, походящий через сечение канала был бы максимальным. Такое сечение, при котором расход будет максимален, называется гидравлически наивыгоднейшим.

Определим, какие из сечений будут гидравлически наивыгоднейшими.

Q = (*)

Для того, чтобы расход был максимален гидравлический радиус должен быть максимален. А максимальный радиус будет при минимальном периметре смоченной поверхности. Определим чему равен гидравлический радиус для этого(*) умножим и поделим на R² .

Q=

гидравлически наивыгоднейшее сечение.

Если = = , R_max =

Наивыгоднейшее гидравлическое сечение:

1. Полукруг: =

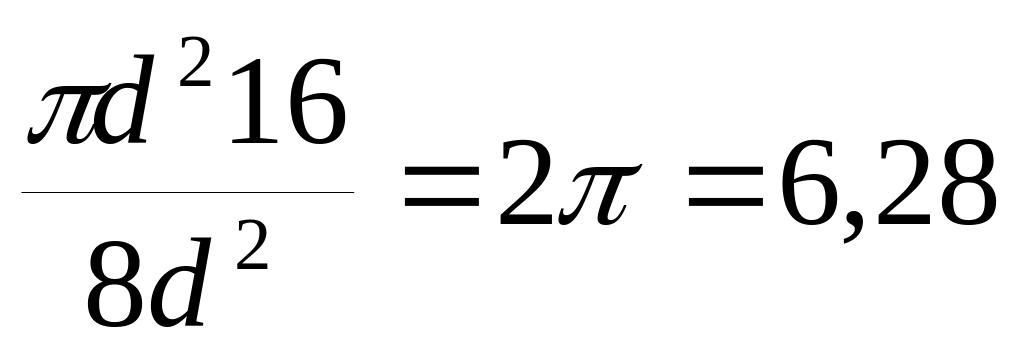
2. Параболический: =6,59

3. Прямоугольный: =8

Гидравлически наивыгоднейшим сечением является полукруг. Но это не так с технико-экономической точки зрения. Наиболее выгодным в строительстве является трапециидальное сечение с необрушаемыми стенками. Каналы одной и той же формы в зависимости от глубины наполнения могут пропускать различный расход. Гидравлически наивыгоднейшим будет являться такое сечение, по которому пройдет максимальный расход. При проектировании каналов стремятся определить максимальный гидравлический радиус.