Ламинарное движение жидкости.

Л аминарное движение является упорядоченным слоистым движением. Так как перемещение жидкости происходит в осевом направлении, а поперечное перемещение отсутствует, то схематично ламинарный поток может представить в виде бесконечно большого числа бесконечно тонких концентрически расположенных цилиндрических слоев, параллельных оси трубопровода и движущихся один внутри другого с различными скоростями, увеличивающимися от стенок к оси.

Слои, которые движутся медленнее, тормозят более быстрые слои.

Рассмотрим кинематическую структуру ламинарного потока и возникшие при этом гидравлические сопротивления. Движения примем установившимися, равномерными. Трубу – круглого поперечного сечения.

P₁ – давление в I-I сечении

σ – касательное напряжение на внутренней поверхности трубы

Р₂ – давление в II-II сечении

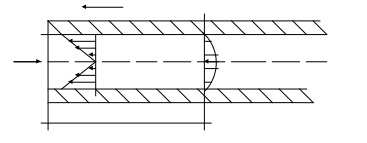τ₀

I II

P₁ r₀ U_max

P₂

I II

L

Определим силы, которые действуют на силы движения равномерно в круглой трубе постоянного диаметра.

P₁ π r₀² – P₂ π r₀² - τ₀2 π r₀L =0.

Касательные напряжения характеризуют силу трения в потоке.

τ₀ = (P₁ – P₂) π r₀²/2 π r₀L = (P₁ – P₂) r₀/2 L.

Для определения (P₁ – P₂) запишем уравнение Бернулли для сечений I-I; II-II. Плоскость сравнения совместим с осью трубы. Жидкость вязкая:

z₁ + p₁ /gρ₁ + α₁U₁²/2g = z₂ + p₂ /gρ₂ + U₂²/2g + h_1-2.

z₁ = z₂ =0

U₁ = U₂

α₁ = α₂

p₁ – p₂ = h_1-2ρg |: L

p₁ – p₂/L = h_1-2ρg /L

τ₀ = h_1-2ρg r₀/2L = iρgr₀/2

Отношение h_1-2/L называется гидравлическим уклоном, то есть потерей энергии, приходящейся на единицу длины.

τ₀ действует по всей внутренней поверхности. Исходя из этого закона распределения касательных напряжений можно получить закон распределения скорости по сечению потока:

τ = μ dU/dr

τ = iρgr/2

μ dU/dr = iρgr/2

dU = iρg/2μ rdr

U=(r₀² – r²)iρg / 2μ Закон распределения скоростей при ламинарном режиме.

r = r₀ → U = 0

r = 0 и U_max = iρg r₀²/ 4μ

Исходя из полученного закона распределения скоростей при ламинарном режиме средняя скорость V = 0,5 U_max.

Продолжение лекции 6

Из V = 0,5 U_max. Можно получить формулу для потери энергии:

V = iρg r₀²/ 8μ =| i=h_1-2/2; μ/ρ = ν; r₀² = d²/4| = hgd²/lν32 , откуда

h = 32 Vlν/ gd²

h – потери на трение при ламинарном движении.

При ламинарном режиме потеря напора по длине прямопропорциональна средней скорости, вязкости и не зависит от характера поверхностей стенок трубы (формулировка Пуазейля).

Для всех режимов движения потерю напора можно определить по формуле :

h = λ lV²/ d2g -формула Дарси

где l – длина трубы;

d – внутренний диаметр;

V – средняя скорость;

λ – коэффициент Дарси –коэффициент гидравлического сопротивления (показывает физический смысл, то есть какая часть скоростного напора теряется за счет трения при прохождении единицы длины l/d)

Для того чтобы определить коэффициент Дарси приравняем формулы Пуазейля и Дарси.

32 Vlν/ gd² = λ lV²/ d2g

откуда λ =64ν/Vd =64/Re (Re = Vd/ν).

Лекция 7