§1. Закони розподілу дискретних випадкових величин

Задають дискретні випадкові величини за допомогою закону розподілу, коли задаються ймовірності їх можливих випадкових значень (див. §1). Залежно від того, за якою формулою будуть обчислюватися ймовірності Р_і, ці закони будуть мати свою назву.

Біноміальний розподіл – це закон розподілу випадкових величин, заданий таблицею, у якій ймовірності Р_і обчислюються за формулою Бернуллі:

(див. лк.23 §1).

Х	0	1	…	і	…	n
р	qn	C1np qn-1	…	C1npi qn-1	…	pn

п

де p, n, q = 1-p, називаються араметрами розподілу.

Математичне сподівання і дисперсія випадкової величини, що має біноміальний розподіл відповідно рівні:

.

Приклад 1. Митний пост дає статистичну оцінку того, що 20% усіх осіб, що повертаються з-за кордону, не декларують весь товар, який підлягає оподаткуванню. Якщо випадково відібрати 5 осіб, то записати закон розподілу випадкової величини Х – кількість осіб, що не декларують весь товар, привезений з-за кордону та знайти математичне сподівання і середнє квадратичне відхилення.

Рішення. В даному випадку р=0,2; q=0,8; n=5.

Тоді

Х	0	1	2	3	4	5
Р	0,32768	0,4096	0,2048	0,0512	0,0064	0,0032

Пуассонівський закон розподілу – це закон розподілу випадкової величини, заданий таблицею, у якій ймовірність обчислюється за формулою Пуассона (див. лк.23, §3).

Х	0	1	…	і	…	n
Р	е-	е-	…		…

де n, =n p.

Типовими прикладами випадкової величини, що має розподіл Пуассона, є: число викликів на АТС за деякий час t; число відновлень складної апаратури за час t, якщо відомо, що відновлення незалежні один від одного і в середньому на одиницю часу випадає  відновлень і т.п.

Розподіл Пуассона залежить від одного параметру , який є математичним сподіванням випадкової величини Х:

.

Дисперсія буде:

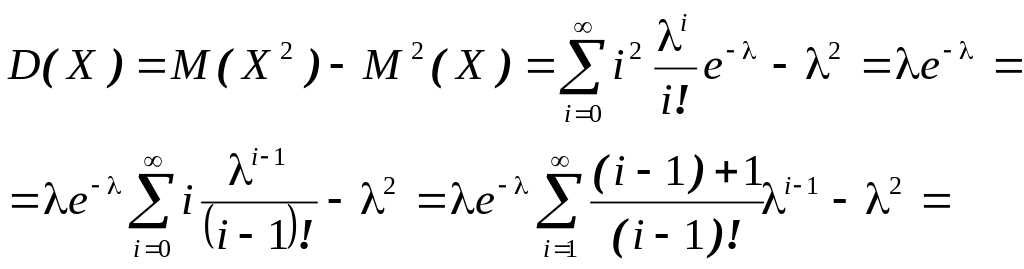
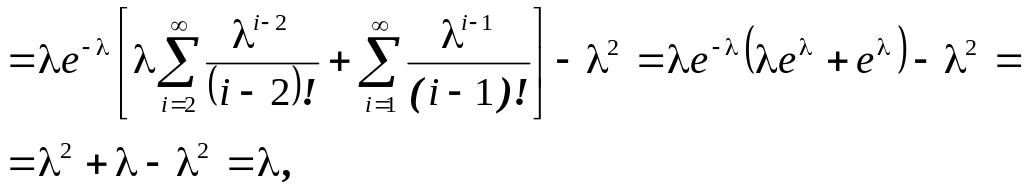
звідси: .

Приклад 2. Завод відправив споживачу 5000 якісних виробів. Ймовірність пошкодження виробу в дорозі рівна 0,0002. Записати закон розподілу чотирьох пошкоджених виробів та зобразити його графічно.

Рішення. З умови: =np=5000 0,0002=1 тому

P₄(0)=0,36788,

P₄(1)=0,36788, P₄(2)=0,0,18394, P₄(3)=0,06131, P₄(4)=0,01533.

Х	0	1	2	3	4
Р	0,36788	0,36788	0,18394	0,06131	0,01533

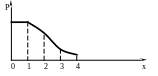
Геометричний закон розподілу

Нехай проводяться незалежні випробування, в кожному з яких ймовірність появи події А рівна р (0 < p < 1), а не появи q = 1- p. Випробування закінчуються, як тільки відбувається подія А. Таким чином, якщо подія А відбулась в k-му випробуванні, то попередніх k-1 випробування Х є: х₁=1, х₂=2, …

Нехай в перших k-1 випробуваннях подія А не відбулася, а в k-му випробуванні з’явилась. Тоді ймовірність рівна

(6)

Покладаючи k=1,2, … у формулі (6), отримаємо геометричну прогресію з першим членом Р і знаменником q (0<q<1): p,qp,q²p, … q^k-1p, … тому розподіл називається геометричним.

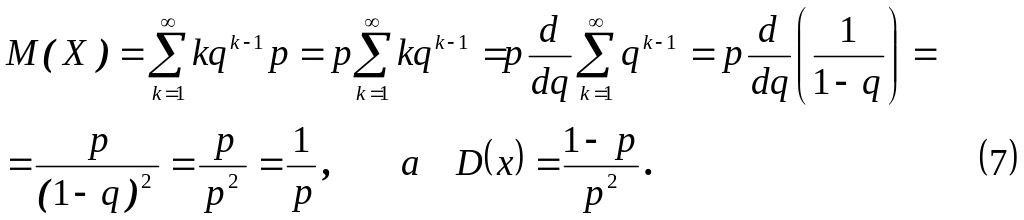
Приклад 3. Проводяться багаторазові випробування елементу на надійність до тих пір, поки він не відмовить в роботі. Ймовірність відмови елементу в кожному випробуванні рівна 0,1. Знайти числові характеристики випадкової величини Х – числа випробувань, які треба провести.

Рішення. По умові р = 0,1. Тому

.