Вариант 17 Задача №1

Предприятие предполагает выпускать два вида продукции А1 и А2, для производства которых используется сырье трех видов. Производство обеспечено сырьем каждого вида в количествах: 848, 532, 432 кг. На изготовление единицы изделия А1 требуется затратить сырья каждого вида 8, 3, 5 кг, соответственно, а для единицы изделия А2 - 6, 5, 2 кг. Прибыль от реализации единицы изделия А1 составляет 25 д. ед., для единицы изделия A2 - 17 д. ед.

Требуется составить план производства изделий А1 и A2, обеспечивающий максимальную прибыль предприятия от реализации готовой продукции.

Требуется:

1. Решить задачу без использования ПЭВМ:

1.Сформулировать и записать математическую модель задачи 1.2. Найти решение полученной модели графически 1.3 Найти решение задачи используя симплекс-метод ("Поиск решения"). Написать выводы.

1.4. Определить интервалы устойчивости полученного решения по отношению к изменению прибыли на единицу продукции 1.5. Определить теневые цены и интервалы их устойчивости по отношению к изменению ресурсов. Указать критическую точку данной производственной модели. 1.6. Оценить стоимость готовой продукции, при изменении сырья каждого вида на величину bi. Найти новый оптимальный план. 1.7. Сформулировать двойственную задачу и найти ее решение. Проверить выполнение теорем двойственности.

2. Решить задачу с помощью пакета MS Exel .

Таблица 1 – Данные к задаче №1

Вид сырья	Продукция		Ограничения по сырью		Изменения запасов
	А1	А2
1-й	8	6	848		74
2-й	3	5	532		-100
3-й	5	2	432		113
Прибыль	25	17

Решение:

1. Пусть - количество вида продукта А₁; - количество вида продукта А₂.

Целевая функция

Составим ограничения:

1.2 Графический метод решения задачи линейного программирования.

Построим многоугольник допустимых решений.

Рисунок 1 -Многоугольник

Определим градиент целевой функции .

Рисунок 2 –Графическое решение

Последней точкой, которой каснется прямая будет точка С. Точка С- оптимальное решение задачи, которое находиться на пересечении прямых и .

Ищем решение системы:

Находим значение целевой функции .

1.3 Симплекс –метод.

Канонический вид задачи

Целевая функция с учетом дополнительных переменных

В качестве базиса выберем .

Таблица 2 - Симплексная таблица 1

Базис	Свободный член	Переменные					Оценочное отношение
	848	8	6	1	0	0	106
	532	3	5	0	1	0	177,(3)
	432	5	2	0	0	1	86,4
Z	0	-25	-17	0	0	0

Так как наибольший по модулю элемент в последней строке (-25), то первый столбец ведущий. В стоблце оценочное отношение находим наименьшее (432/5=86,4). Третья строка ведущая и 5 – разрешающий элемент. Вместо в базис вводим .

Таблица 3- Симплексная таблица 2

Базис	Свободный член	Переменные					Оценочное отношение
	1564/5	0	24/5	1	0	-13/5	56
	2724/5	0	34/5	0	1	-3/5	7115/19
	862/5	1	2/5	0	0	1/5	216
Z	2160	0	-7	0	0	5

Текущий опорный план неоптимален, так как в индексной строке находится отрицательный элемент. Ведущий столбец – второй. Минимальное оценочное отношение – 56. 2⁴/₅ разрешающий элемент. . В базис вместо вводим .

Таблица 4- Симплексная таблица 3

Базис	Свободный член	Переменные					Оценочное отношение
	56	0	1	5/14	0	-4/7
	60	0	0	-15/14	1	14/7
	64	1	0	-1/7	0	3/7
Z	2552	0	0	21/2	0	1

Последняя строка не содержит отрицательных элементов, значит данный план оптимальный , по таблице Z_max=2552, Х^*=(64,56;0;60; 0).

Необходимо производить 64 шт. продукта А1 и 56 шт. продукта А2. Максимальная прибыль 2552 ден. ед. Данное решение совпадает с решением, полученным графическим методом.

1.4 Воспользуемся приложением «Поиск решения» и определим интервалы устойчивости полученного решения по отношению к изменению прибыли на единицу продукции.

Рисунок 3- Интервалы устойчивости полученного решения

Нормированная стоимость – это дополнительные двойственные переменные. Они показывают, насколько по модулю уменьшится целевая функция при принудительном выпуске единицы данной продукции. Нормированная стоимость для каждого продукта А1 и А2 равняется нулю, то есть целевая функция не уменьшиться при принудительном выпуске единицы данных видов продукции. И продукт А1 и продукт А2 рентабельны.

Допустимое увеличение показывает, насколько максимально можно увеличить коэффициент целевой функции (то есть цену продукта), чтобы структура оптимального плана осталась прежней. Допустимое уменьшение, наоборот, показывает, насколько можно максимально уменьшить коэффициент целевой функции, чтобы осталась прежней структура оптимального плана. То есть, чтобы выпуск продукта А1 оставался рентабельным, максимально допустимое увеличение его цены составляет примерно 17,5 ден. ед. Допустимое уменьшение 2,33 ден. ед. Чтобы выпуск продукта А2 оставался рентабельным, максимально допустимое увеличение его цены составляет приблизительно 1,75 ден. ед., допустимое уменьшение 7 ден. ед.

1.5.

Рисунок 4- Теневая цена

Теневая цена показывает, как изменится целевая функция при изменения запаса ресурса на единицу. Если ресурс использован полностью, то теневая цена этого ресурса положительна. В нашем примере полностью используются ресурсы вида 1 и 3, и их теневые цены положительны. Если мы увеличим запас 1-го вида сырья на единицу, то ЦФ возрастёт на 2,5 ден. ед., если мы увеличим запас 3- го вида сырья на единицу, то ЦФ возрастёт на 2 ден.ед.

Рисунок 5– Отчет по результатам

Несвязанным ограничением является второе ограничение. Это говорит о том , что сырье 2 не используется полностью в процессе производства данных продуктов. Недоиспользование ресурса составляет 60 ед.

Рисунок 6– Отчет по пределам

Если будет выпускаться продукт А1, то значение прибыли будет составлять 952 ден.ед. Если будет выпускаться продукт А2 значение прибыли будет составлять 1600 ден.ед.

1.6 Оценим стоимость готовой продукции, при изменении сырья каждого вида на заданную в условии величину.

, - матрица, состоящая из столбцов первоначального базиса ( ) последней симплекс-таблицы:

Получаем, ; ; .

.

Все компоненты вектора неотрицательны , то есть выполняется условие

Значит, при заданных изме­нениях запаса сырья двойственные оценки не изменятся. Это говорит о том, что первый и третий виды сырья будут использоваться полностью, поэтому первое и третье неравенства исходной системы с измененными правыми частями можно записать как систему уравнений: .

Подставляем новый план в целевую функцию: Z _{нов. max} (102;18)=25*102+17*18=2850 ден. ед.

7. Составим двойственную задачу.

2-ая теорема двойственности.

Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения.

1-ая теорема двойственности.

Если одна из взаимодвойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их линейных функций равны: Z_max.

Решение двойственной задачи дает оптимальную систему оценок ресурсов.

Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи Y = C*A^-1.

Матрица A состоит из компонентов векторов, входящих в оптимальный базис.

Как видно из последнего плана симплексной таблицы, обратная матрица A^-1 расположена в столбцах дополнительных переменных .

Тогда Y = C*A^-1 =

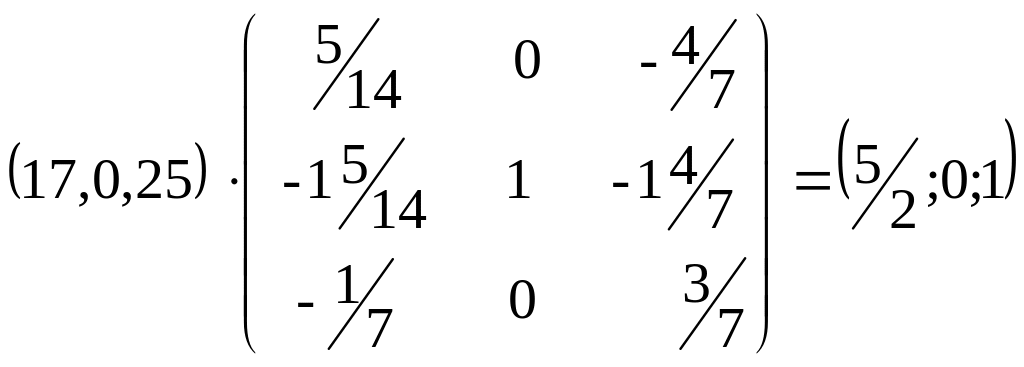
Оптимальный план двойственной задачи равен: y₁ = 2¹/₂; y₂ = 0; y₃ = 1.

Как видим, оптимальное решение двойственной находится в индексной строке последней симплекс-таблицы и столбцах, соответствующих первоначальному базису.

Z(Y) = 848*2¹/₂+532*0+432*1 = 2552. Получаем, что Z_max.

Теоремы двойственности выполняются.