§ 6.1. Интегральные оценки
Интегральные оценки качества используются для интегрального, суммарного оценивания качества переходных процессов систем управления. Чаще всего их используют не для определения показателей качества, а для сравнения вариантов одной и той же системы, так как есть основания полагать, что если интегральная оценка меньше, то качество системы выше.
Определение. Под интегральными оценками обычно понимают скалярные величины, вычисляемые по формулам:
,
,
,
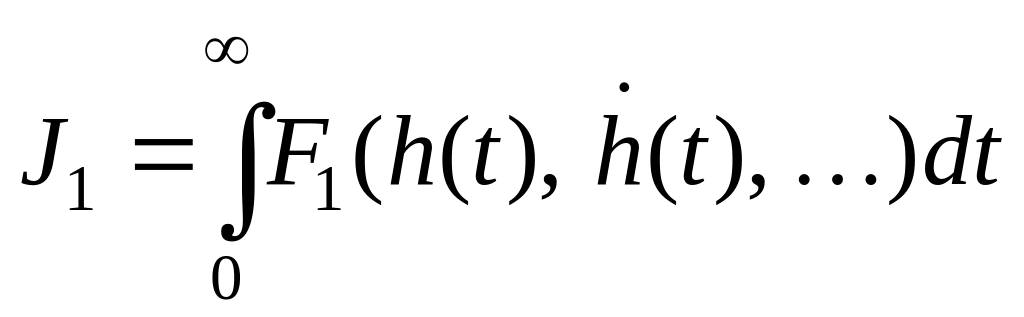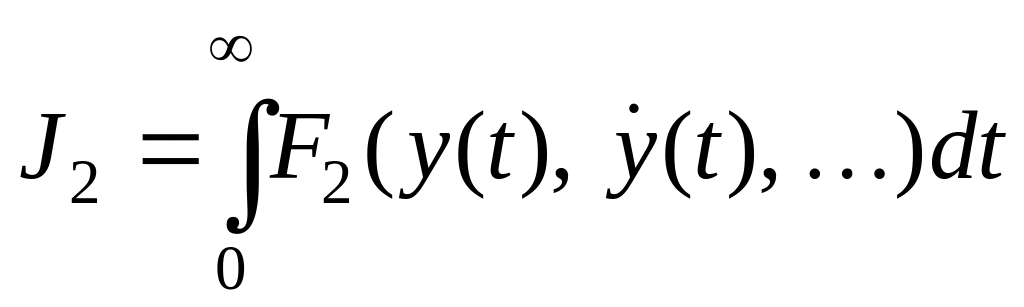где
– линейная, а
и
– квадратичные функции своих аргументов.
Иногда интегральные оценки называют критериями качества или функционалами качества. В общем случае интегральные оценки можно вычислить как по коэффициентам передаточных функций, так и по коэффициентам уравнений системы в переменных состояния.
Наиболее простая линейная интегральная оценка имеет вид
,
(6.1)
где
– переходная функция исследуемой
системы.
Фактически
– это площадь, заключенная между
графиками функций
и
.
Как видно на рис. 6.1, если
,
то и
.
Другими словами, чем меньше оценка
,
тем меньше время регулирования
.
Преимущество интегральных оценок перед
прямыми показателями качества
заключается в том, что они непосредственно
связаны с варьируемыми параметрами
регулятора.
Это позволяет
аналитически, как и при минимизации
СКО, найти такие значения этих параметров,
при которых, например, время регулирования
будет минимальным. Для этого, очевидно,
достаточно так выбрать параметры
регулятора, чтобы интегральная оценка
была минимальной.
Недостаток линейной интегральной оценки (6.1) заключается в том, что она позволяет оценить показатели качества только при монотонных переходных процессах. Поэтому на практике более распространёнными являются квадратичные интегральные оценки. В частности, квадратичная интегральная оценка может иметь вид
.
(6.2)
Геометрический
смысл этой оценки показан на рис. 6.2. Как
видно, на этом рисунке оценка
– это так называемая «квадратичная
площадь» между графиками функций
и
(заштрихованные участки на рис. 6.2 имеют
положительные «квадратичные» площади).
Поэтому эта оценка пригодна для
исследования свойств как монотонных,
так и колебательных переходных процессов.
Недостатком
квадратичной интегральной оценки
является то, что она приближается к
своему оптимальному значению, т.е. к
нулю, если только переходная функция
системы приближается к единичной
функции. Но практически переходную
функцию вида
реализовать невозможно. Поэтому в
конкретных задачах нереализуемость
функции
приводит к тому, что с уменьшением
квадратичной оценки увеличиваются и
перерегулирование, и колебательность
системы. Это показано на рис. 6.3, где
.
В
связи с этим часто применяют улучшенную
квадратичную
интегральную оценку, при которой
подынтегральная функция включает и
производные от переходной функции. Эта
оценка определяется следующим образом.
Пусть
.
Тогда выражение
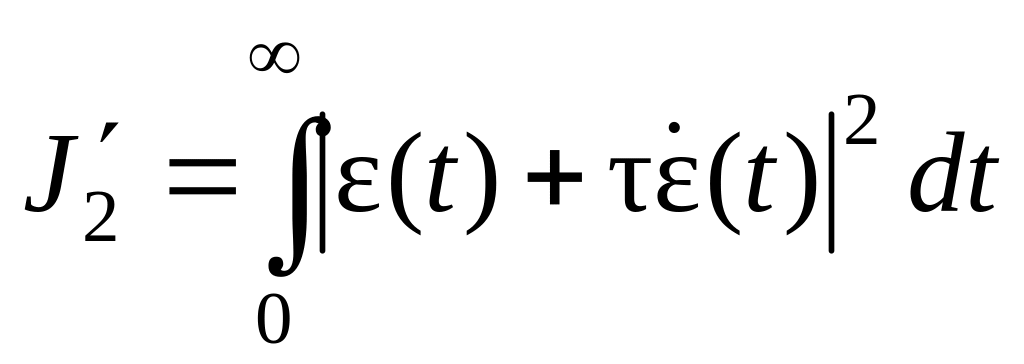(6.3)
будет представлять улучшенную квадратичную оценку переходной функции системы.
Из
формулы (6.3) видно, что оценка
достигает минимального нулевого
значения, когда переходная функция h(t)
становится равной экспоненциальному
процессу
(кривая 1, рис. 6.4). Этот рисунок соответствует
системам, параметры которых таковы, что
.
Как видно, выбор параметров системы из
условия минимума улучшенной квадратичной
оценки приводит к повышению быстродействия
системы без увеличения перерегулирования
и колебательности h(t).
Интегральную квадратичную оценку (6.2) можно выразить через коэффициенты уравнений в переменных состояния системы следующим образом. Предположим, уравнения системы заданы в виде:
, 
.
Как
известно,
при
и нулевых начальных условиях. Следовательно,
при
и
.
Если
,
то
,
и равенство (6.2) принимает вид
.
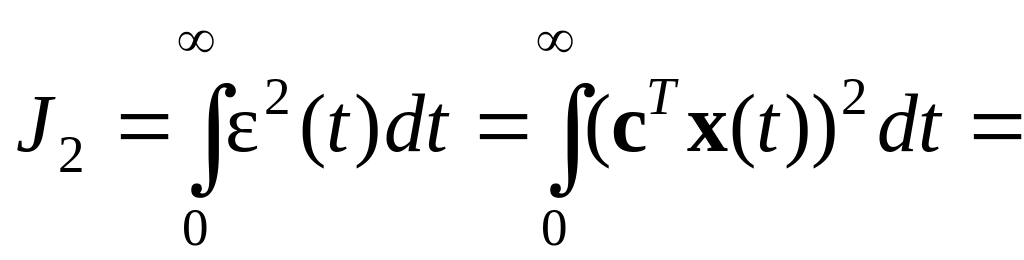
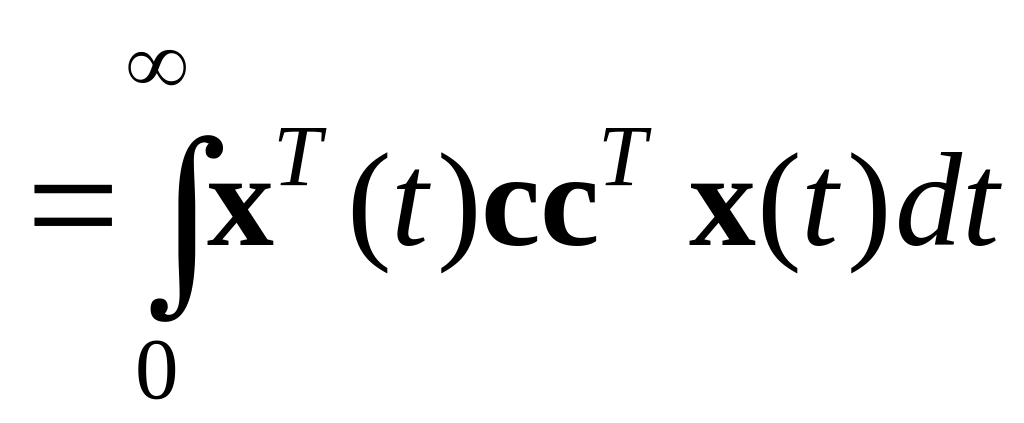В общем случае это выражение записывается следующим образом:
,
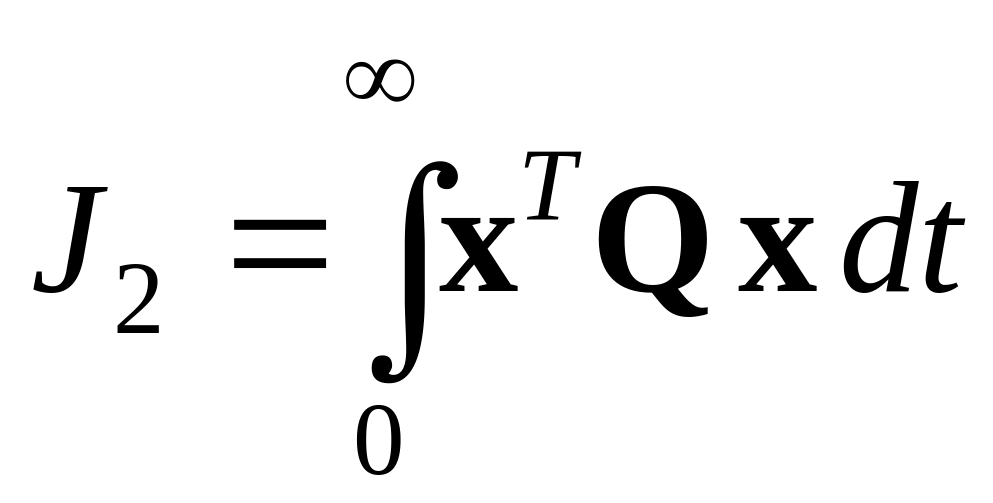(6.4)
где Q – некоторая симметрическая положительно полуопределенная матрица, т.е. матрица, собственные числа которой либо больше, либо равны нулю. В предыдущем выражении эта матрица, очевидно, равна произведению вектора-столбца c на вектор-строку cT.