§ 5.8. Определение случайных ошибок при векторных воздействиях

Перейдём к определению статистических характеристик выходных переменных динамических систем в установившемся режиме в случае случайных векторных воздействий.

При этом будем предполагать, что рассматриваемая система (рис. 5.15 при ψ = 0), является многомерной, т.е. имеет несколько входов и несколько выходов. Причем прямая связь между входами и выходами отсутствует, т.е. будем считать, что уравнения системы в переменных состояния имеют вид

, , (5.65)

где , и – векторы, а A, B и C – матрицы соответствующих размерностей.

Применяя формулу Коши к системе (5.65), получим

,

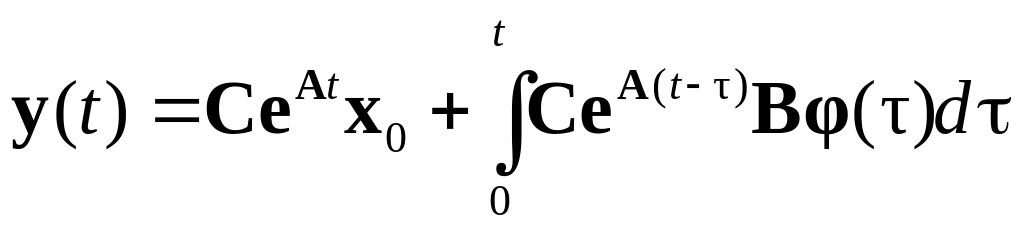где – переходная матрица системы (5.65).

Будем рассматривать систему (5.65) при нулевых начальных условиях, т.е. при . Тогда из предыдущего выражения следует равенство

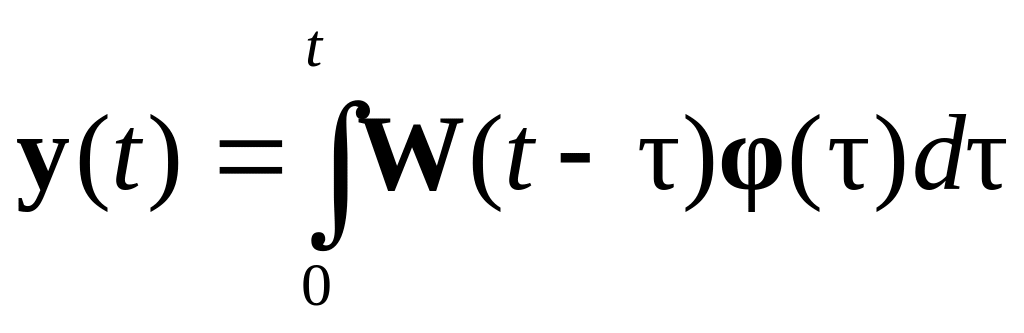. (5.66)

где – матричная переходная импульсная функция рассматриваемой системы. Каждый i-й столбец этой матрицы представляет собой реакцию системы (5.65) на входной вектор , у которого i-я компонента является дельта-функцией, т.е. , а остальные равны нулю.

Переходя к определению искомых характеристик, прежде всего, отметим, что вектор выходных величин (5.66) системы (5.65) фактически является реализацией некоторого случайного векторного процесса. Поэтому, применяя сначала операцию усреднения к выражению (5.66), найдем, что вектор средних значений выходного процесса определяется выражением

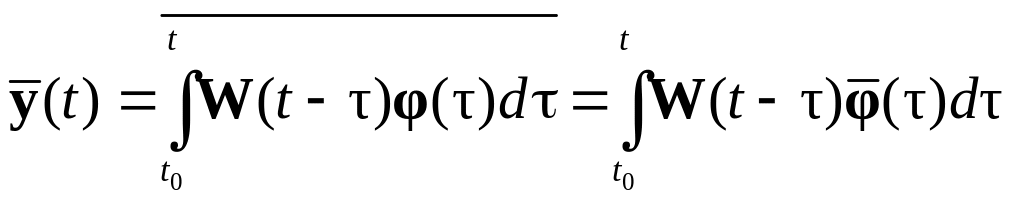. (5.67)

Из выражения (5.66) следует, что если входной процесс системы (рис. 5.15) является случайным стационарным векторным процессом, то ковариационная матрица выхода динамической системы, являющегося тоже случайным стационарным векторным процессом, определяется равенством

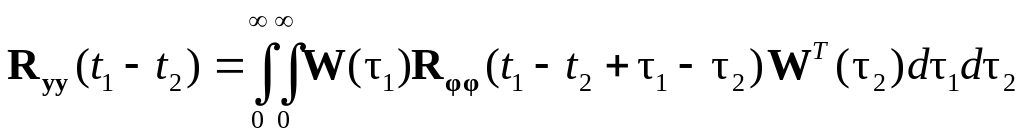. (5.68)

Здесь предполагается, что соответствующие интегралы существуют.

В результате преобразования по Фурье выражения (5.68) получается формула для определения матрицы спектральной плотности выходного случайного векторного стационарного процесса системы (5.65) следующего вида:

, (5.69)

где – комплексная передаточная матрица динамической системы (5.65), а – спектральная матрица случайного входного векторного процесса этой же системы. По аналогии с выражениями (5.58), (5.59) из (5.69) выводим

. (5.70)

Полученные соотношения позволяют определить статистические характеристики выходных переменных линейных динамических систем в установившемся режиме, т.е. по истечении времени переходного процесса в начале функционирования системы.

Переходные процессы при случайных воздействиях. Перейдем к анализу влияния случайных воздействий на линейные динамические системы в переходных режимах.

Приведём сначала некоторые соотношения теории случайных векторных процессов. Пусть – случайный векторный процесс типа белого шума с матрицей интенсивности , , и – заданные детерминированные, функциональные матрицы, а Q – весовая симметрическая положительно определённая матрица (см. §12.3). Тогда справедливы соотношения

,

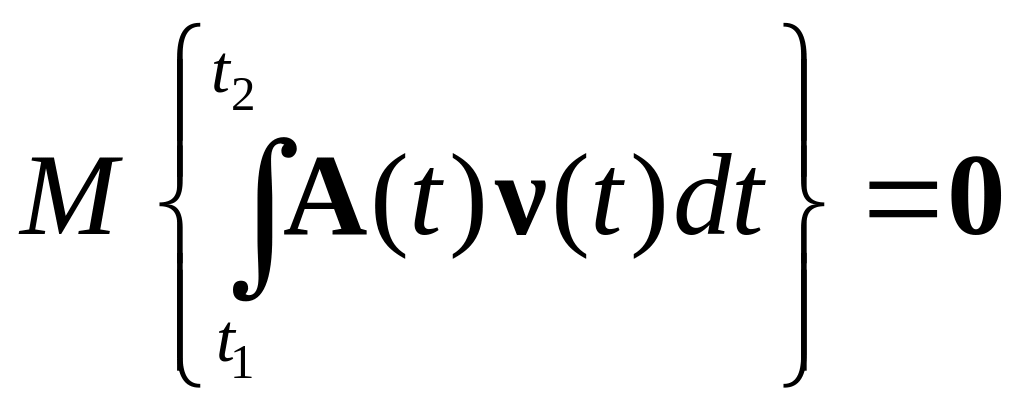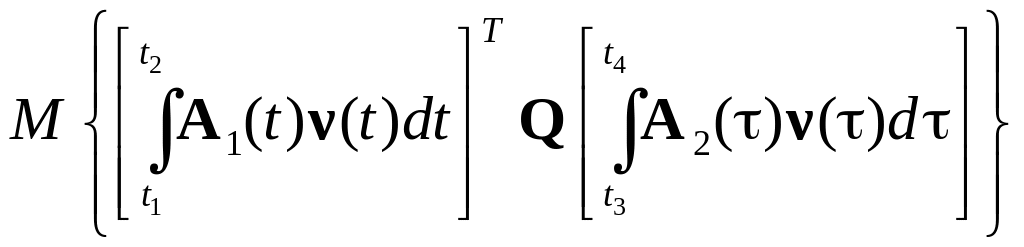
, (5.71)

где I – пересечение интервалов и ; – след матрицы ;

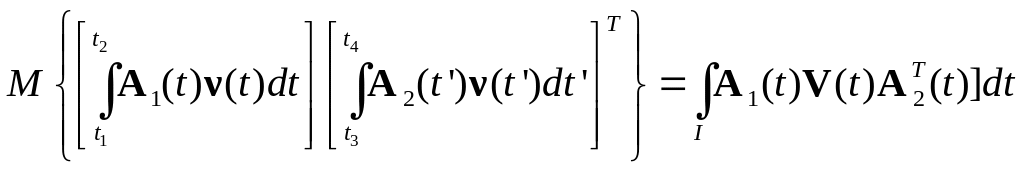. (5.72)

Соотношения (5.67) – (5.72) используются обычно при исследовании влияния случайных векторных воздействий на различные динамические системы.

Далее рассмотрим некоторую линейную динамическую систему с постоянными параметрами, на вход которой поступает случайный векторный процесс типа белого шума. Уравнение состояний системы аналогично первому уравнению (5.65):

, , (5.73)

где – центрированный белый шум с матрицей интенсивности , а – случайная векторная величина, независимая от . Вектор её средних значений равен , а матрица дисперсий равна , т.е. , а , где – символ математического ожидания.

Будем предполагать, что собственные числа постоянной матрицы A в (5.73) имеют отрицательные вещественные части. Тогда справедливо равенство

, (5.74)

где – переходная матрица системы (5.73).

При этих условиях с помощью формулы Коши, приведённой выше, и первого равенства (5.71) можно найти, что изменения вектора средних значений переменных состояния системы определяется выражением

, (5.75)

то есть монотонно затухает с ростом времени t.

Аналогично с помощью (5.72) можно установить, что симметрическая квадратная матрица дисперсий процесса удовлетворяет дифференциальному матричному уравнению

, (5.76)

и определяется выражением

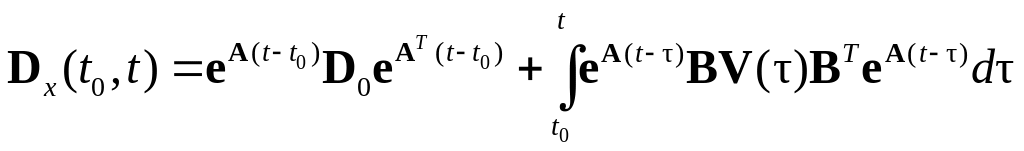. (5.77)

Если , то при условии (5.74) существует предел матрицы при . Этот предел определяется следующим равенством

, (5.78)

причём матрица удовлетворяет матричному алгебраическому уравнению Ляпунова вида

. (5.79)

Таким образом, дисперсия вектора переменных состояния линейной динамической системы с постоянными параметрами, на входе которой действует случайный векторный процесс типа белого шума, является переменной величиной, т.е. зависит от времени. Если переходная матрица системы удовлетворяет условию (5.74), а входной белый шум является стационарным, то дисперсия с ростом t стремится к некоторой постоянной матрице . Причём эта матрица – матрица установившихся дисперсий компонент вектора состояния может быть найдена либо с помощью интеграла (5.78), либо из алгебраического уравнения (5.79).

С помощью выражений (5.71), (5.72) можно также установить, что если Q и Q₁ – постоянные симметрические неотрицательно определенные матрицы, а в (5.73) , то при всех существует симметрическая матрица такая, что

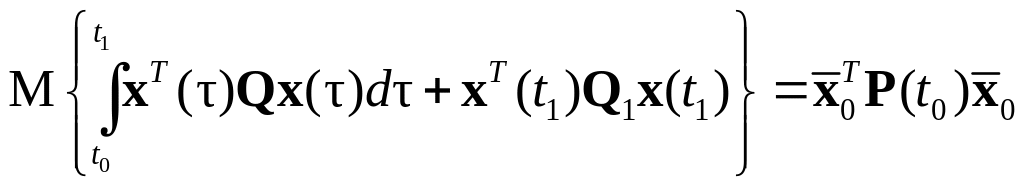. (5.80)

При этом указанная матрица определяется равенством

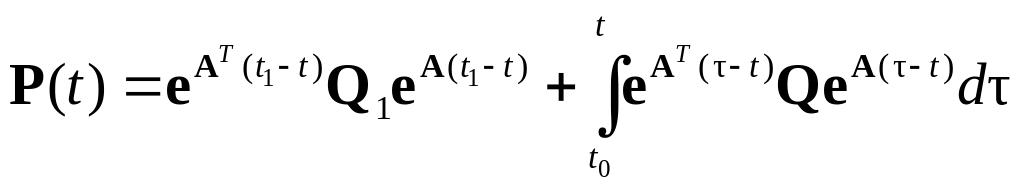(5.81)

и удовлетворяет дифференциальному матричному уравнению Риккати

, (5.82)

с конечным условием .

Аналогично, если в (5.73) матрица A такая, что выполняется условие (5.74), то существует предел

, (5.83)

причём – постоянная матрица, являющаяся решением матричного уравнения Ляпунова

.

Отметим, что если матрица Q является положительно определённой, т.е. , то при условии (5.74) решение уравнения Ляпунова – матрица , т.е. также является положительно определённой.

Приведённые выражения (5.75) – (5.83) позволяют исследовать поведение линейных многомерных систем под влиянием случайных воздействий в переходных режимах. Приведём численный пример, ограничившись, для наглядности, случаем одномерной динамической системы первого порядка.

Пример 4.2. Рассмотрим систему, которая описывается дифференциальным уравнением

, (5.84)

где коэффициент ; , причём – случайная величина со средним значением и дисперсией ; – некоррелированный со случайной величиной центрированный белый шум интенсивности , т.е. случайное воздействие с нулевым средним и дисперсией .

Найти функции и , описывающие изменения во времени среднего значения и дисперсии переменной состояния динамической системы (5.84).

Решение. В данном случае переходной матрицей системы является экспонента . Поэтому, подставляя её в выражения (5.75), (5.77) и полагая , , и , найдём

, (5.85)

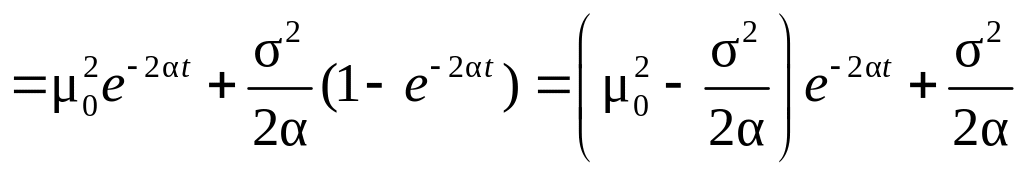. (5.86)

Графики изменения величин и , соответствующие выражениям (5.85) и (5.86),

приведены на рис. 5.17. На этом рисунке:

кривая 1 – зависимость при ,

кривая 2 – зависимость при .

Как видно из графиков, приведенных на рис. 5.17, при , т.е. при выполнении условия (5.74), среднее значение переменной состояния системы монотонно стремится к нулю.

Практически можно считать, что через время величина .

Дисперсия также изменяется с течением времени. Однако эта функция стремится к некоторому не нулевому значению, которое определяется дисперсией входного воздействия и параметром динамической системы.

Весьма существенно то, что время установления дисперсии (длительность переходного процесса по дисперсии) примерно в два раза меньше – времени установления среднего значения переменной состояния (см. рис. 5.17). Можно показать, что такое соотношение указанных времён, при выполнении условия (5.74), справедливо при любом порядке системы.

Из равенства (5.85) следует, что установившееся значение дисперсии переменной состояния системы (5.84) равно . Аналогичное выражение можно получить и из соотношения (5.79), которое в рассматриваемом случае имеет вид

.

Отсюда также следует, что .

Это же выражение можно получить и с помощью формулы (5.70), если принять, что . Действительно, передаточная функция системы (5.84) , а спектральная плотность входного воздействия . Следовательно, в данном случае , и по формуле (5.70) имеем

.

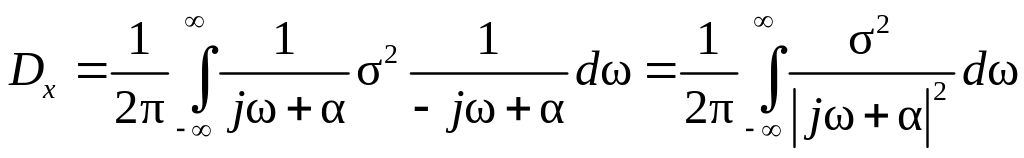Сравнивая полученное выражение с равенством (5.61) и применяя формулу Мак-Ленна при , , и , снова получим .

Таким образом, уже при , где – время затухания переходной матрицы системы, статистические характеристики переменных динамических систем с постоянными параметрами можно вычислять по формулам, полученным для установившихся режимов.

Г л а в а 6

КОСВЕННЫЕ ОЦЕНКИ КАЧЕСТВА САУ