§ 5.7. Вычисление ско при скалярных воздействиях.

Параметрическая оптимизация

Так как инвариантность систем управления не всегда достижима, то часто, в особенности при наличии случайных воздействий, применяются оптимальные системы, которые строятся таким образом, чтобы ошибка была минимально возможной.

Рассмотрим основные особенности систем данного типа, когда и задающее воздействие и возмущение являются случайными. Как показано выше, точность систем управления при случайных воздействиях определяется среднеквадратической ошибкой (СКО).

Схема определения этой ошибки показана на рис. 5.13. На этом рисунке – по-

прежнему, выходная переменная эталонной системы; – выходная переменная реальной системы; и – случайные задающее воздействие и возмущение; – сигнал ошибки системы. Как и , и переменная – это случайный процесс, который характеризуется следующими величинами: дисперсией, корреляционной функцией и спектральной плотностью. Среднее значение этого процесса чаще всего принимается равным нулю.

Обычно СКО обозначается (см. § 5.3) буквой и вычисляется через спектральную плотность сигнала ошибки в соответствии с выражением

. (5.58)

Подчеркнём, что интеграл в этом выражении вычисляется по формулам, приведенным ниже.

При этом, если возмущение , т.е. отсутствует (см. рис. 5.13), то спектральная плотность сигнала ошибки рассматриваемой здесь системы определяется известным равенством

, (5.59)

где – передаточная функция по ошибке от воздействия , – спектральная

плотность случайного процесса .

В системах управления обычно действуют несколько случайных воздействий, поэтому для определения общей СКО системы и получения единого подхода к её вычислению все случайные воздействия обычно приводятся к входу системы, как показано на рис. 5.13. Другими словами, на этом рисунке – это задающее случайное воздействие с заданной спектральной плотностью , и средним значением ; а – это суммарное возмущающее воздействие, приведённое к входу системы, причём . Кроме спектральных плотностей и обычно задается и – взаимная спектральная плотность. При этом , если процессы и независимы.

Найдем . По схеме на рис. 5.13 можно записать

или

.

По формулам, аналогичным (5.58), (5.59), отсюда выводится выражение для дисперсии (среднего квадрата) случайной ошибки

. (5.60)

Как отмечалось выше, передаточные функции линейных систем управления обычно являются отношением полиномов. С другой стороны, спектральные плотности случайных сигналов являются четными функциями частоты . Поэтому интегралы в (5.58) и в (5.60) всегда могут быть приведены к виду

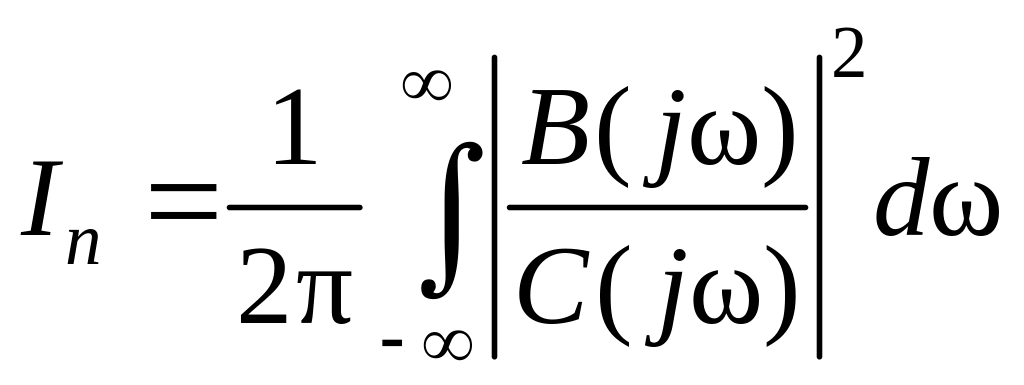, (5.61)

где , – полиномы от , причем , а полином – гурвицев, т.е. удовлетворяет критерию Гурвица.

Интеграл (5.61) является табличным и найден в общем виде для . Соответствующие формулы называются формулами Мак-Ленна и приводятся в литературе по теории управления. Приведем здесь эти формулы для некоторых значений n:

,

,

,

. (5.62)

Формулы Мак-Ленна, формально, позволяют взять интеграл (5.61) при . Однако уже при применение этих формул не рационально из-за их громоздкости. В этих случаях целесообразнее применять следующую более компактную формулу, справедливую для произвольного n:

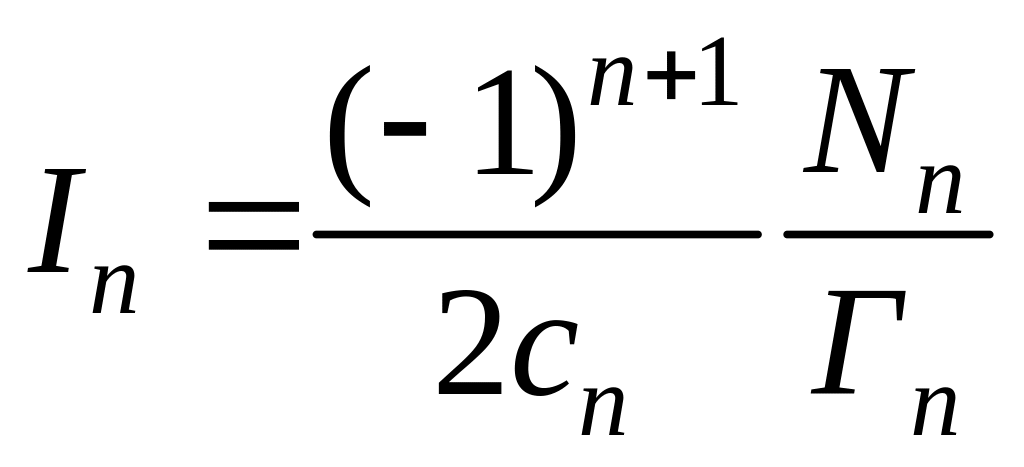. (5.63)

Здесь , .

Здесь g_i – коэффициенты полинома

.

Приведённые выражения (5.62) и (5.63) позволяют не только вычислять значения СКО при заданных параметрах, но и проводить параметрическую оптимизацию, т.е. находить такие значения варьируемых параметров системы управления, при которых её СКО имеет минимальное значение.

Такие значения параметров называются оптимальными, а система управления с этими значениями параметров (а значит, и с минимальной СКО) называется оптимальной.

Пример 5.8. Найти значение СКО следящей системы, структурная схема которой приведена на рис. 5.14. При этом , , , , .

Решение. Прежде всего отмечаем, что поскольку система следящая, то . Далее, так как возмущение приложено не ко входу рассматриваемой системы (как на рис. 5.13), то, чтобы воспользоваться формулой (5.60), необходимо преобразовать структурную схему заданной системы к виду, показанному на рис. 5.15.

Непосредственно по рис. 5.14 можно записать

.

Отсюда выводим

или

. (5.64)

Обозначим

. (5.65)

В соответствии с равенством (5.65), очевидно, можно считать, что – это выходная переменная линейного звена, на входе которого действует случайное воздействие . Поэтому, при-

меняя формулу (5.59) к (5.65), при Т = 0,5 найдем .

С учетом обозначения (5.65) уравнению (5.64) соответствует некоторая динамическая система, структурная схема которой изображена на рис. 5.15, причём передаточная функция этой системы определяется выражением .

Так как по условиям задачи , то сигналы и на рис. 5.15 также является не коррелированными, т.е. .

Теперь к исследуемой системе можно применить общую формулу (5.60). Подставляя соответствующие выражения и численные значения параметров, получим

.

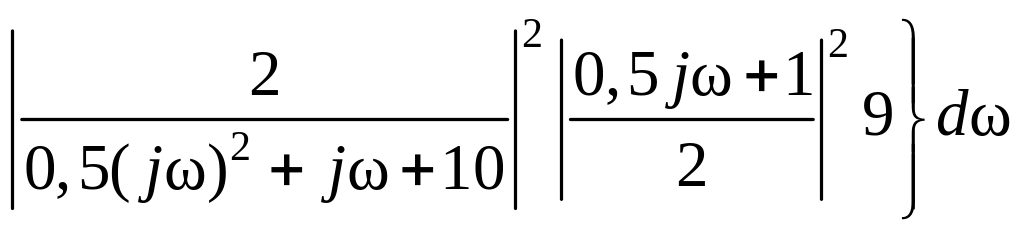Чтобы упростить вычисление дисперсии, разобьем этот интеграл на сумму двух интегралов и вычислим их в отдельности с помощью формул Мак-Ленна (5.62) при и :

.

Далее

.

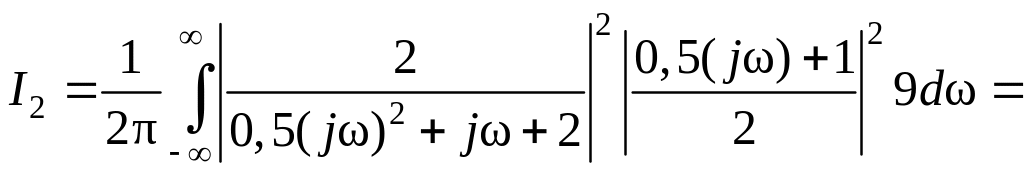
Итак, среднеквадратическая ошибка . ■

Интегралы, содержащиеся в приведённом выше выражении для дисперсии случайной ошибки , удобно вычислять в MATLAB. Чтобы показать порядок соответствующих действий, представим выражение для следующим образом:

,

, .

Интеграл вычисляется в MATLAB путём ввода следующих команд:

% вычисление квадрата модуля w_ε1(jω)

w = sym('w', 'real');

Wy1 = (j*w +0.5*(j*w)^2)/(2 + j*w + 0.5*(j*w)^2);

Wy2 = abs(Wy1)^2;

% вычисление дисперсии D_δ1

Sff = 100/(w^2+100);

Dy1 =int(Wy2*Sff, w, -inf, inf)/2/pi;

Dy1 = simple(Dy1)

% результат

Dy1 = 5.645

% вычисление квадрата модуля w_ε2(jω)

Wy3 = (1 + 0.5*j*w)/(10 + j*w + 0.5*(j*w)^2);

Wy4 = abs(Wy3)^2;

% вычисление дисперсии D_δ2

Dy2 =int(Wy4, w, -inf, inf)/2/pi;

Dy2 = simple(Dy2)

Dy2 = 0.5

Dy = Dy1 + 9*Dy2

% результат

Dy = 10.145

Полученное значение, очевидно, соответствует найденному выше результату.

Приведем также пример на определение оптимального значения параметра системы управления.

Пример 5.9. Найти оптимальное значение коэффициента усиления системы управления (см. рис. 5.13), если

, ,

а спектральные плотности задающего воздействия и приведенного к входу системы возмущения определяются выражениями

, , .

Решение. Так как в данном случае возмущение приведено к входу рассматриваемой системы, то для определения дисперсии ошибки системы можно воспользоваться непосредственно выражением (5.60). Подставляя заданные выражения, получим

.

Разбивая, как и выше, интеграл в этом выражении на два и применяя формулы Мак-Ленна (5.62), придём к выражению

.

Для определения оптимального значения k продифференцируем это выражение по k и приравняем полученную производную нулю. После упрощений получим следующее уравнение:

.

Положительный корень этого уравнения определяет оптимальное значение . При этом значении k дисперсия , а СКО . Для наглядности полученного результата на рис. 5.16 приведена зависимость дисперсии , из которой видно, что при найденном значении дисперсия случайной ошибки имеет минимум. ■

Подчеркнем ещё раз, что рассмотренный метод определения параметров оптимальной системы называется методом параметрической оптимизации. Он применяется в тех случаях, когда структура системы полностью известна, и для завершения процесса расчета системы необходимо определить значения её варьируемых параметров. Структура системы при этом определяется на основе опыта проектирования и в общем случае может оказаться не рациональной.

Для получения оптимальной структуры и оптимальных значений параметров систем управления необходимо применять методы структурной оптимизации. Некоторые из них рассматриваются ниже.