. (5.13)

Отсюда видно, что каждый коэффициент ошибки является коэффициентом пропорциональности между i-й производной воздействия и вкладом этой производной в ошибку системы, вызванную данным воздействием.

Метод коэффициентов ошибки удобно использовать в тех случаях, когда входное воздействие, задающее или возмущающее, имеет конечное число ненулевых производных по времени. Например, если задающее воздействие является полиномиальным типа (5.11), то все его производные по времени, порядок которых выше , тождественно равны нулю, т.е.

, , , .

В этом случае ряд (5.13) оказывается конечным, что позволяет вычислять ошибку, вызванную таким воздействием по формуле:

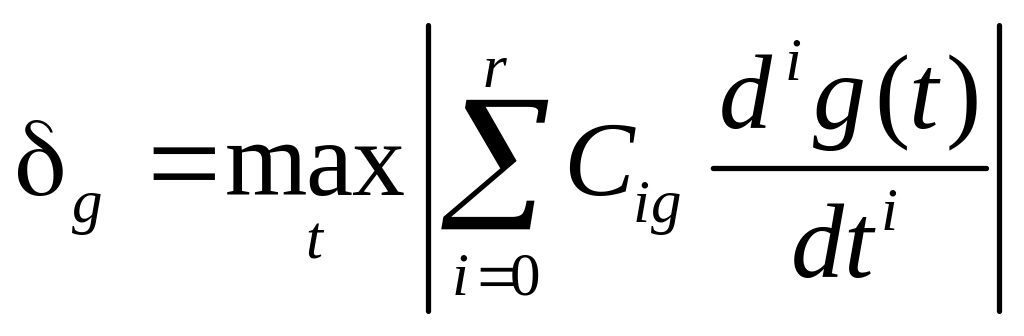. (5.14)

В связи с этим метод коэффициентов ошибки чаще всего применяют в случае полиномиальных воздействий как задающих, так и возмущающих.

Определение передаточных функций по ошибке. Уравнения систем управления в переменных состояния с одним задающим воздействием g и одним возмущением f, как известно, имеют вид

(5.15)

(5.16)

Передаточные функции «вход-выход» системы (5.15), (5.16) вычисляются по формулам:

, (5.17)

. (5.18)

Пусть , т.е. система является следящей, системой стабилизации или программного управления. В этом случае , поэтому передаточные функции по

ошибкам, вызванным воздействиями g и f, с учетом (5.17), (5.18) будут равны

, (5.19)

. (5.20)

Если же система рассматриваемого типа задана непосредственно передаточными функциями и , то в этом случае

, . (5.21)

Допустим, также задана структурная схема системы, приведённая на рис. 5.9, и передаточные функции

, , (5.22)

где , , , – некоторые полиномы. Тогда на основе структурной схемы, полагая начальные условия нулевыми, можно записать следующие равенства:

, (5.23)

. (5.24)

Исключим из уравнений (5.23), (5.24) изображение . Тогда

или

. (5.25)

Следовательно, для рассматриваемой структурной схемы

, (5.26)

или с учетом (5.22)

, .

Из этих выражений следует, что передаточные функции по ошибкам линейных систем

также являются отношением полиномов от переменной р. Если из уравнений (5.23), (5.24) исключить , то получим формулы для определения передаточных функций «вход-выход» системы, структурная схема которой соответствует рис. 5.9:

, . (5.27)

Из (5.25) – (5.27) вытекают приведённые выше соотношения (5.21).

Вычисление коэффициентов ошибки. Приведенные выше формулы для коэффициентов ошибки не удобны для практического применения, так как включают операции дифференцирования дробно рациональных функций. Приведём вывод гораздо более удобных формул. Рассмотрим сначала случай задающего воздействия. Пусть

. (5.28)

Тогда после разложения в ряд Тейлора получим равенство

.

Далее умножим это равенство на полином и приравняем коэффициенты в средней и в правой части полученного равенства при , , и т.д. В результате получим равенства

, , , .

Из этих равенств последовательно находим

, , , _. (5.29)

Часто систему желательно построить так, чтобы младшие коэффициенты ошибки по задающему воздействию равнялись нулю. Очевидно, для этого необходимо выполнение следующих равенств:

, , , . (5.30)

Формулы для вычисления коэффициентов ошибки по возмущению f через коэффициенты передаточной функции по ошибке имеют тот же самый вид, т.е. если

, (5.31)

то

, , , , (5.32)

так как знак минус в выражении (5.31) не влияет на величину ошибки (5.14).

Если структурная схема исследуемой системы отличается от приведенной на рис. 5.9, то для определения передаточных функций по ошибкам целесообразно сначала одним из методов, рассмотренных в § 2.7, привести схему системы к этому виду. Другими словами, сначала целесообразно найти передаточные функции «вход-выход» типа (5.27), а затем воспользоваться формулами (5.21), (5.29) и (5.32).

Пример 5.3. Для системы, рассмотренной в примере 5.1, найти скоростную ошибку по задающему воздействию при .

Решение. Так как система задана своей передаточной функцией , то по формуле (5.21) имеем

.

Так как степень заданного воздействия , то согласно (5.14) для вычисления ошибки достаточно найти два коэффициента ошибки: и . Поэтому по формулам (5.29) находим , . Учитывая, что в данном случае , по формуле (5.14) получим . ■

При синтезе систем удобно пользоваться формулами, которые связывают коэффициенты ошибки с коэффициентами передаточных функций «вход-выход» (5.21), определяемых выражениями (5.17), (5.18) или (5.27). Пусть эти функции представлены следующим образом:

, (5.33)

. (5.34)

Тогда из выражений (5.26) с учетом (5.33) и (5.34) имеем

, (5.35)

. (5.36)

Сравнивая (5.35) и (5.36) с правыми частями (5.28) и (5.31), найдем по (5.29) и (5.32), что в данном случае формулы для коэффициентов ошибки по задающему воздействию принимают вид

, , , . _(5.37)

Коэффициенты ошибки по возмущению f и в этом случае вычисляются по формулам (5.32).

Пример 5.4. Найти ошибку следящей системы с отрицательной единичной обратной связью (рис. 5.9) и с передаточной функцией

по задающему воздействию .

Решение. Прежде всего, по первой формуле (5.27) найдем

.

Так как , то найдем только коэффициенты , и по формулам (5.37):

, , .

В данном случае , , , поэтому по формуле (5.14) ошибка системы .

Отметим, что в данном случае можно было бы воспользоваться и первой формулой (5.26), а затем формулами (5.29). ■

Таким образом, полученные выражения (5.25) – (5.37) позволяют методом коэффициентов ошибки вычислять ошибки систем, заданных структурными схемами.

Если же система задана уравнениями в переменных состояния (5.15), (5.16), то можно сначала найти передаточные функции (5.17), (5.18) или (5.19), (5.20) и воспользоваться приведёнными выше формулами. Однако можно вычислить коэффициенты ошибки и непосредственно по коэффициентам уравнений (5.15), (5.16), пользуясь следующими формулами:

, , , (5.38)

, , . (5.39)

Пример 5.5. Найти полную ошибку следящей системы, которая описывается уравнениями (5.15), (5.16), где

, , , , .

Задающее воздействие , а возмущение .

Решение. Так как система задана уравнениями в переменных состояния, то воспользуемся формулами (5.38), (5.39), а также (5.14) и формулой для (5.10).

В данном случае степень задающего воздействия равна 1, поэтому согласно (5.14) необходимо найти два коэффициента ошибки С_0g и C_1g. Подставляя численные значения в формулы (5.38), найдем С_0g = 0, а C_1g = 0,2. Производная , поэтому по формуле (5.14) имеем .

Возмущение имеет нулевую степень, поэтому достаточно найти лишь коэффициент . Подставляя значения в (5.39), получим . Теперь, заменяя в формуле (5.14) g на f , найдем . Наконец, подставляя найденные значения и в формулу (5.10), найдем искомую суммарную ошибку исследуемой системы . ■

Условия равенства нулю коэффициентов ошибки. На основе формул (5.29) и (5.37) заключаем: для того, чтобы коэффициентов ошибки по задающему воздействию g системы (5.15), (5.16) или заданной передаточными функциями (5.21), (5.27), тождественно равнялись нулю, необходимо, чтобы:

а) младших коэффициентов числителя передаточной функции по ошибке (5.28) равнялись нулю;

б) младших коэффициентов числителя , , , передаточной функции системы по задающему воздействию (5.33) равнялись коэффициентам знаменателя , , , той же передаточной функции.

Таким образом, ; , если

; , (5.40)

или

; . (5.41)

Аналогично из соотношений (5.32) следует, что по отношению к возмущению f справедливы условия ; , если

; , (5.42)

где – коэффициенты полинома числителя передаточных функций (5.31) или (5.34) рассматриваемой системы управления.

Аналогичные условия на матрицу А, векторы b, c и числа β, η из уравнений (5.15), (5.16) следуют из формул (5.38), (5.39).

Так как воздействия, приложенные к системе (см. рис. 5.9), обычно имеют малые значения высших производных, то для получения приемлемой точности часто бывает достаточно обеспечить нулевые значения коэффициента , а иногда и . Такие системы, как отмечалось выше, называются астатическими.

§ 5.5. Статические и астатические системы

Определение. Система управления называется статической по данному воздействию, если её коэффициент ошибки по этому воздействию не равен нулю. Это означает, что статическая ошибка системы пропорциональна этому воздействию.

Система управления называется астатической по некоторому воздействию, если по этому воздействию её коэффициент , т.е. её статическая ошибка по этому воздействию равна нулю и не зависит от него. Если система имеет -й порядок астатизма по некоторому воздействию, то она имеет нулевых коэффициентов ошибки по этому воздействию. Таким образом, равенства (5.40), (5.41) можно рассматривать как условия астатизма порядка по задающему воздействию, а равенства (5.42) – по возмущающему воздействию.

Условия обеспечения астатизма. Часто возникает вопрос, какой должна быть структура системы, чтобы она имела заданный порядок астатизма. С целью получения ответа на этот вопрос рассмотрим систему управления, структурная схема которой приведена на рис. 5.10.

Пусть , т.е. система является следящей, а полиномы передаточных функций, приведённых на рис. 5.10, таковы, что и , а . При этом система является устойчивой. Найдем связь между структурой системы, её порядком астатизма и её коэффициентами ошибки.

По задающему воздействию. В соответствии со схемой (рис. 5.10) и первым выражением (5.25) можно записать

.

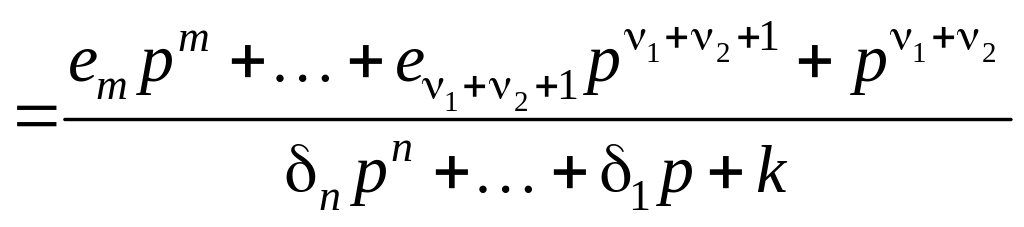Здесь – коэффициенты числителя и знаменателя передаточной функции соответственно.

Так как в числителе полученного выражения коэффициентов равны нулю, то в соответствии с выражениями (5.29) данная система имеет нулевых коэффициентов ошибки по задающему воздействию. Следовательно, её порядок астатизма по этому воздействию .

Итак, для системы с единичной, отрицательной обратной связью, порядок астатизма по задающему воздействию и число нулевых коэффициентов ошибки всегда равны числу «чистых» интеграторов в прямой цепи системы. Справедливо и обратное утверждение.

Поэтому для построения системы с порядком астатизма по задающему воздействию необходимо выбрать такой регулятор, чтобы в прямой цепи системы получилось «чистых» интеграторов, т.е. звеньев с передаточной функцией .

Отметим также, что если , то первый ненулевой коэффициент ошибки по задающему воздействию всегда равен

. (5. 43)

В этом выражении – коэффициент передачи системы в разомкнутом состоянии, равный

.

Система является статической по задающему воздействию, если , тогда

. (5.44)

Из этих выражений видно, что для уменьшения ошибки системы необходимо увеличивать порядок астатизма и коэффициент усиления системы в разомкнутом состоянии. Однако коэффициент усиления можно увеличивать лишь до тех пор, пока система ещё будет иметь необходимый запас устойчивости.

По возмущающему воздействию. В соответствии со схемой, приведенной на рис. 5.10, можно записать

.

Так как (см. (5.27)), то при передаточная функция по ошибке от возмущения имеет вид

.

При этом, если , то

; . (5.45)

Здесь – число чистых интеграторов в прямой цепи системы (рис. 5.10), включенных между выходом сравнивающего устройства и точкой приложения возмущения .

Таким образом, порядок астатизма системы (рис. 5.10) по возмущению и число нулевых коэффициентов ошибки по нему, определяются числом чистых интеграторов, включенных между точкой измерения отклонения и точкой приложения возмущающего воздействия . Если таких интеграторов нет, т.е. , то данная система является статической по отношению к возмущению . При этом, если , то

, при . (5.46)

Условия нулевой или постоянной ошибки при полиномиальных воздействиях. Рассмотрим условия, при которых линейная динамическая система управления будет иметь нулевую или постоянную ошибку по некоторому (задающему или возмущающему) полиномиальному воздействию.

Предположим, воздействие описывается выражением (5.11), т.е. полиномом от t степени r. Как показано выше, в этом случае производная по времени , а все производные при всех .

Поэтому на основе соотношений (5.41) и (5.43) можно сделать вывод: для обеспечения нулевой ошибки, обусловленной полиномиальным воздействием r-й степени, необходимо чтобы система имела -й порядок астатизма по этому воздействию, т.е. необходимо, чтобы по этому воздействию порядок астатизма .

Если же необходимо обеспечить постоянную по величине ошибку, обусловленную полиномиальным воздействием r-й степени, то порядок астатизма системы по этому воздействию должен быть равен степени r данного воздействия, т.е. необходимо, чтобы .

При этом ошибка системы, например, по задающему воздействию (5.11) при и , в соответствии с формулой (5.42), определяется выражением

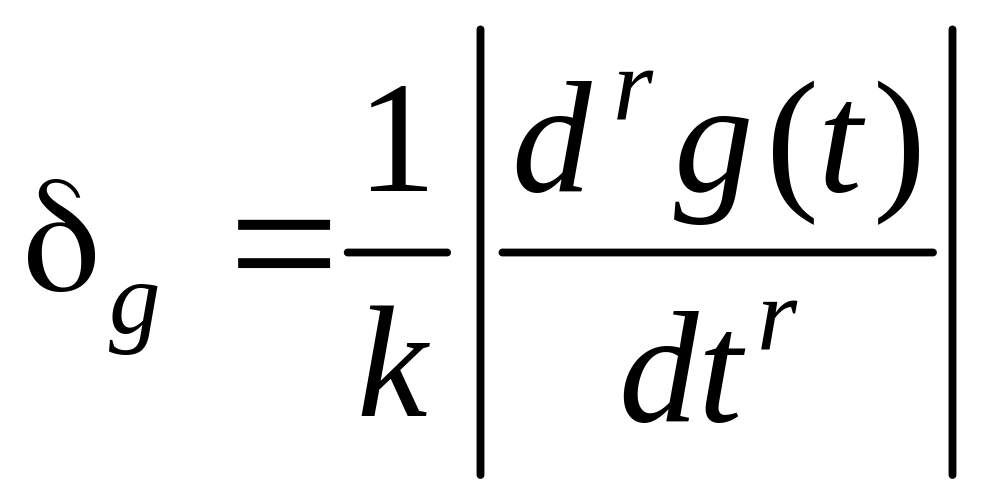. (5.47)

Пример 5.6. Пусть в (5.11) , а , т.е. . Тогда при , и по формуле (5.14) . В то же время при ошибка системы как по (5.14), так и по (5.47) будет равна , т.е. будет ненулевой, но постоянной, как показано на рис. 5.11. ■

Таким образом, выбирая достаточно высокий порядок астатизма по тому или иному воздействию, можно обеспечить желаемую ошибку системы по этому воздействию. Если при этом система строиться с применением управления по выходу и воздействиям (см. § 8.1), то снимается проблема обеспечения устойчивости, несмотря на высокий порядок астатизма.