3. Шарообразный вакуумный домен во внешних магнитном и спиновом полях

Задача о ВД в виде шара в однородных магнитном и спиновом полях в случае отсутствия вещества, когда следует положить в уравнениях (83) μ = 1;  μ_G = 1, аналогична задаче о ВД в виде шара в однородных электрическом и гравитационном полях, также при отсутствии вещества. Поэтому за исключением обозначений в обеих задачах будет одинаковым внешний вид исходных уравнений, граничных условий, условий на бесконечности. Необходимо лишь принять во внимание отличия определений магнитной и спиновой индукций от определений электрической и гравитационной индукций. Если D = ε₀E + P; D_G = ε_0GE_G + P_G, то B = μ₀H + μ₀M; B_G = μ_0GH_G + μ_0GM_G; B_G = μ_0GH_G + μ_0GM_G. Таким образом, аналогом P является μ₀M, а аналогом P_G, очевидно, μ_0GM_G.

Следует также учесть, что поскольку c = (ε₀μ₀)^-1/2 = (ε_0Gμ_0G)^-1/2, то

кг/Kл.

Заметим, что коэффициент η₀ входит во многие формулы электрогравидинамики [3, 4, 6].

Итак, с учетом указанных отличий задач о шаре- ВД в однородных электрогравитационном и магнитоспиновом полях при отсутствии вещества аналогом (92) будут соотношения:

(96₁)

(96₂)

где H₀, H_0S - однородные магнитное и спиновое поля вне шара- ВД соответственно; H_i, H_Si магнитное и спиновое поля внутри шара соответственно; a_μ = μ₁(μ₀μ_0G)^-1/2.

Используя указанную аналогию, в рассматриваемом случае следует определить магнитную M_M и спиновую M_S поляризации так:

(97)

Из (97) и (96) вытекает, что

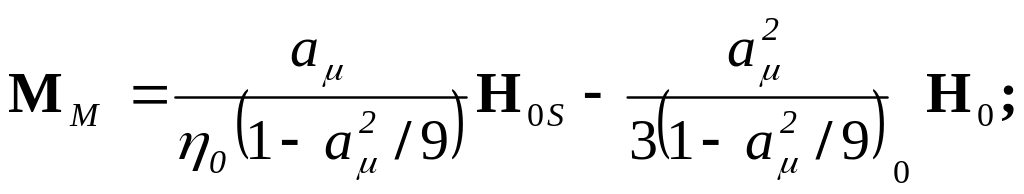(98₁)

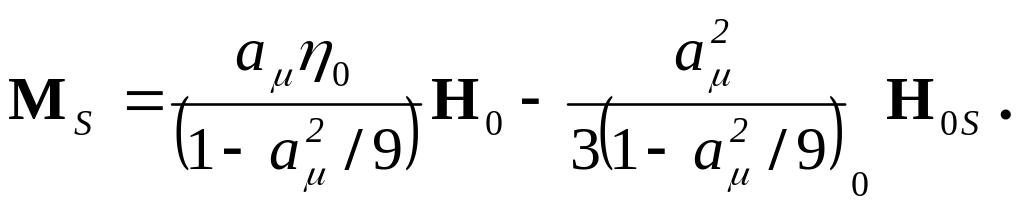(98₂)

Компоненты магнитного поля вне шара- ВД, возникающего при появлении поляризации M_М, в сферической системе координат (r, θ’, α’) с полярной осью z’,ориентированной по направлению поляризации M_M имеют вид:

(99₁)

(99₂)

где l_M = M_MV - магнитный момент ВД; V- объем шара- ВД; M_M - модуль вектора M_M.

Компоненты спинового поля вне шара- ВД от поляризации M_S в сферической системе координат (r, θ”, α”) с полярной осью z'', ориентированной по направлению поляризации M_S, представим аналогично предыдущим соотношениям:

(100₁)

(100₂)

где l_S = M_SV - спиновой момент ВД; M_S - модуль вектора M_S.

Если выражения для полей H_i, H_Si, согласно (96), полные, то компоненты полей H_e(M_M), H_Se(M_S) необходимо суммировать с компонентами однородных полей H₀, H_0S.

3.2.4. Энергия вакуумного домена в электрическом, гравитационном, магнитном и спиновом полях

Наиболее важным результатом решения задач о ВД в виде шара в электрo-гравитационном и магнито-спиновом однородных полях является определение двух диполей ВД – электрического d и гравитационного d_G, и двух моментов ВД - магнитного l_M и спинового l_S. Согласно (91) вектор d направлен по направлению поляризации P_GE, вектор d_G по направлению поляризации P_EG; а согласно (97), l_M направлен по направлению поляризации M_S, вектор l_S по направлению поляризации M_M.

Определение диполей и моментов ВД (моменты ВД можно также назвать магнитным и спиновым диполями) позволяет определить энергию ВД, связанную с четырьмя полями: E₀, E_0G, H₀, H_0S.

Классический расчет энергии уединенного диполя в электрическом поле выполнен в теории электричества Таммом [61]. На основе этого расчета энергию ВД, как четырехдиполя в четырех полях, следует представить в виде:

(101)

где

Согласно (93) энергии W_E, W_G выразим таким образом:

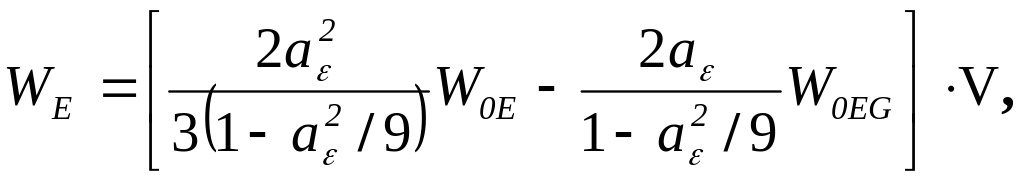(102)

где

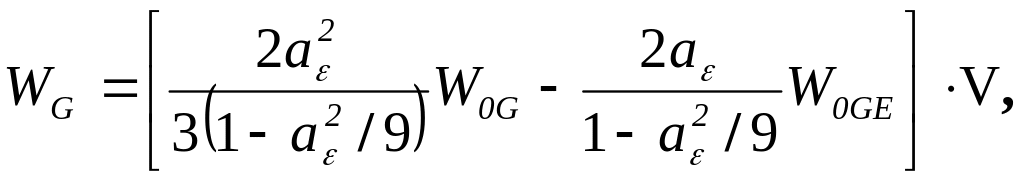(103)

где

Согласно (98) энергии W_M и W_S можно представить так:

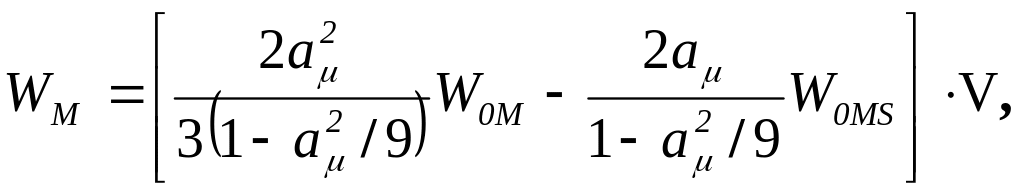(104)

где

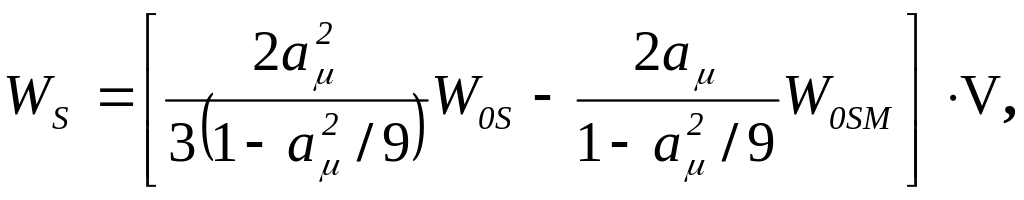(105)

где

Поля E₀, E_0G, H₀, H_0S вообще говоря, зависят от пространственных координат, но их можно приближенно считать константами в пределах ВД. Поэтому действующие на ВД дипольные силы можно определить следующим образом [61]:

(106₁)

(106₂)

(106₃)

(106₄)

где  оператор градиента.

Эти дипольные силы уже были рассмотрены, но не были определены в предыдущей главе при изучении уравнения движения ВД.