Из рассмотренных треугольников скоростей вытекают следующие очевидные соотношения:

; ; (1.29) ; ; (1.30)

При записи формул (1.29) для входного треугольника скоростей и формул (1.30) для выходного треугольника скоростей принято, что проекции скоростей и положительны, если их направление совпадает с направлением окружной скорости, и отрицательны, если они направлены в противоположную сторону.

2. Тепловой расчет осевой турбинной ступени

При общности физической стороны рабочего процесса в ступенях паровых и газовых турбин методики их теплового расчета формально различны. В значительной мере это связано с несовпадением уравне­ний, которые описывают состояние водяного пара в паровых турбинах и продуктов сгорания, расширяющихся в газовых турбинах. Для ступе­ней паровых турбин используется метод расчета, основанный на урав­нении состояния в виде диаграммы I – S. Ступени газовых турбин рассчитываются аналитически, с применением - диаграмм и таб­лиц термогазодинамических функций.

В практике конструкторских бюро тепловые расчеты проточных частей и ступеней паровых турбин ведутся с использованием I - S - диаграммы на ЭВМ.

В целях наглядности далее приводится порядок расчета ступени паровой турбины с построением характерных состояний рабочей среды, т.е. водяного пара, в I - S - диаграмме.

2.1. Рабочий процесс в соплах, его построение в I - s – диаграмме и определение скоростей

При выполнении расчета турбинной ступени исходные данные для решения прямой, обратной или смешанной задач могут задаваться по-разному. В любом случае они должны быть достаточны для решения за­писанных выше уравнений состояния, неразрывности и энергии. Обычно при решении смешанной задачи задаются следующие величины:

- параметры торможения перед ступенью ;

- статическое давление за ступенью ;

- расход рабочей среды через ступень G;

- частота вращения ротора n;

- средний диаметр облопачивания D_СР;

- углы и ;

- термодинамическая степень реактивности ступени .

При таком задании исходных данных состояние рабочей среды на входе в ступень находится легко; на I - S - диаграмме (рис.2.1) его отмечают точкой .

Зачастую вместо параметров торможения задают статические пара­метры на входе в ступень , и скорость на входе в сопла С₀. В этом случае состояние движущего газа на входе в ступень обозначается на диаграмме I - S точкой О.

После этого вычисляют изоэнтропический перепад энтальпий , Дж/кг, соответствующий скорости С₀ : . Отложив его значение вверх от точки О, находят положение точки О^* и энтальпию торможения в соответствии с известным уравнением:

. (2.1)

Найденная точка О^* определяет и термические параметры тор­можения и .

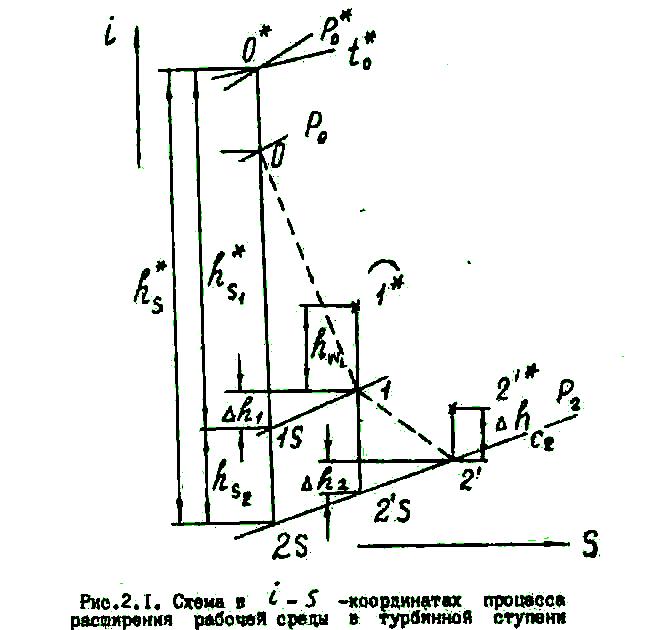
Изоэнтропа, проведенная на диаграмме I - S из точки О, дает на пересечении с изобарой точку 2S, характеризующую состояние рабочего тела за ступенью при изоэнтропическом процессе в ней.

Располагаемый изоэнтропический перепад энтальпий в ступени по статическим параметрам на входе в нее и на выходе записывается выражением: , а по параметрам торможения перед ней и статическим параметрам за ней:

. (2.2)

Пересечение изоэнтропы 0^*-2S с изобарой в точке 1S (см. рис.2.1) определяет состояние рабочей среды на выходе из сопел при изоэнтропическом процессе расширения. При этом:

. (2.3)

Здесь (подобно ранее показанному ) – располагаемый изоэнтропический перепад энтальпий в сопловом аппарате.

Кроме того,

, (2.4)

где - располагаемый изоэнтропический перепад энтальпий на рабочих лопатках по статическим параметрам перед и за рабочим вен­цом.

Определим понятие «термодинамическая степень реактивности» ступени:

. (2.5)

При заданном значении легко найти , поскольку, как видно на рис.2.1, .

Теоретическая скорость выхода потока из сопел в сечении 1-1 при изоэнтропическом расширении

. (2.6)

Из-за наличия необратимых потерь механической энергии в соп­лах действительная скорость истечения всегда меньше теоретической.

Используя формулу (1.21) для коэффициента скорости, можно най­ти действительную скорость выхода потока из сопел:

. (2.7)

Вводя в рассмотрение «коэффициент потерь энергии» в соплах

, (2.8)

можно найти абсолютную величину необратимых потерь механической энергии в соплах , которые, превращаясь в тепло, повышают энтальпию рабочей среды, выходящей из сопел:

. (2.9)

Поэтому действительное состояние рабочей среды в сечении 1-1 определяется точкой 1 на изобаре (рис.2.1). При этом:

. (2.10)

Условно линия процесса расширения в соплах изображается пря­мой 0-1. Следует заметить, что равенство (2.8) является приближенным и соответствует характеристике в рамках одномерной теории.

Величина находится на основании исследований процессов истечения из реальных сопел*.

Следующим шагом расчета ступени является построение входного треугольника скоростей. Исходными данными для этого служат:

- окружная скорость на среднем диаметре облопачивания

; (2.11)

- скорость выхода потока из сопел С₁ найденная выше;

- заданный угол .

Построение треугольника скоростей позволяет определить скорость и угол .

^{Примечание *}Коэффициенты потерь, если они не заданы, определяются при выборе облопачивания в процессе расчета, или по формулам (1.24).