5.2. Нерасчетные режимы ступеней паровой турбины при работе их в составе отсека

Особенностью промежуточных ступеней отсека является зависи­мость граничных условий, определяющих процесс в ступени, от мес­та (или номера) ступени в отсека, поскольку режам ее работы определяется режимом работы отсека. Учитывая это, экспериментальные характеристики промежуточной ступени корректно получать на основе испытаний ее в составе натурного или модельного отсека. Сказанное особенно существенно для нерасчетных режимов. При постановке опытов и исследовании их результатов возникает ряд вопросов, связанных с представлением экспериментальных характеристик. Значительная их часть вызвана тем, что испытания отсеков являются интеграль­ными, течение - пространственным, а постановка задачи при определении характеристик - одномерной. Эти противоречия острее всего могут проявлять себя в случае отсека ступеней ЦНД.

Рассмотрим некоторые аспекты представления интегральных характ-ристик отсека и ступеней ЦНД на основе экспериментальных ис­следований отсека натурных размеров на паре.

Интегральные характеристики ступеней и отсека эксперименталь­ного ЦНД - результаты опытов, в процессе которых измерены параметры пара в контрольных сечениях перед сопловым венцом первой ступени и за рабочим венцом последней ступени, а также интегральная мощность, развиваемая отсеком, и расход пара через него. Теплообмен между паровым потоком и окружающей средой не учитывается.

Характеристики упомянутого ЦНД будем представлять, используя методы классической термодинамики. Из-за сложности процессов течения в многоступенчатых отсеках и недостаточной точности их мате­матического описания информацию о переменных режимах ступеней и отсека представим, привлекая теорию подобия.

Условимся об используемых понятиях и допущениях. Течение в контрольных сечениях ЦНД и во всех его межвенцовых зазорах полагаем установившимся, а состояние пара - равновесным.

Термическое состояние пара в данной точке пространства опре­деляется давлением Р и температурой Т, измеряемыми в процес­се опытов. Все остальные свойства пара являются их функциями. Кине­матика потока в той же точке характеризуется модулем вектора ско­рости и его направлением, которые также находятся во время опытов. Наличие термических и кинематических параметров позволяет судить о термогазодинамическом состоянии парового потока в фиксированной точка. Совокупность этих состояний во всех точках сечения произволь­ного межвенцового зазора отсека определяет интегральное термодина­мическое состояние потока в этом сечении*. Наличие термогазодинани-ческих состояний потоков во всех межвенцовых зазорах и в контроль­ных сечениях отсека ЦНД позволяет интегрально задать процесс из­менения упомянутого состояния пара от входа в отсек до выхода из него (для краткости: интегральное изменение состояния среды в ЦНД),

Состояние потока в сечении произвольного межвенцового зазора можно трактовать с двух позиций. В представлениях метода Лагранжа оно является следствием всех процессов, имевших место от контроль­ного (на входе) до рассматриваемого сечения. В представлениях мето­да Эйлера это состояние при установившемся режиме течения функция только положения сечения в проточной части.

* Переход от упомянутой совокупности к осреднениям по сечению параметрам, определяющим данное состояние, может быть сделан исходя из формул, приведенных выше в разд.I.I.

Изменение состояния пара от одного сечения до другого опреде­ляется выбором этих сечений. Конкретному интегральному изменению состояния среды между входным и выходным сечениями ЦНД соответст­вуют воздействия на нее окружающей срады на твердых границах про­точной части и в упомянутых сечениях. Параметры потока, измерен­ные в них, оказываются одновременно параметрами и окружающей и рабочей среды. При адиабатичности течения в ЦНД их значения - итог всех процессов, происходящих между контрольными сечениями отсека, результатом которых является работа, совершаемая потоком на твер­дых поверхностях проточной части. В связи с этим, при одинаковом расходе рабочей среды через все ступени отсека ее состояния в конт­рольных сечениях определяют интегральное изменение состояния среды в ЦНД. Любой паре состояний парового потока на входе и выходе из ЦНД соответствует единственное интегральное изменение состояния среды в нем.

В качестве контрольных могут рассматриваться и сечения в произвольных межвенцовых зазорах отсека, что позволяет распространять все сказанное на любую группу ступеней (или ступень) в его пределах и определять ее интегральные характеристики на основе измерений па­раметров потока в этих сечениях.

При изменении режима работы отсека ЦНД по сравнению с расчет­ным, взаимодействие потока с окружающей средой может изменяться за счет

- изменения геометрических очертаний проточной части;

- изменений относительных скоростей ее подвижных и неподвиж­ных границ;

- воздействия внешней среды в контрольных сечениях;

- отборов пара между ступенями отсека.

При выполнении опытов на одной и той же экспериментальной установке исходят из тождественности границ проточной части. В слу­чае испытаний на паре натурных ступеней и отсеков ЦНД энергетичес­ких турбин частота вращения ротора постоянна. Переменность ее при моделировании на паре и воздухе учитывается дополнительно. По вели­чине расхода пара режимы работы делятся на безотборные, с одинако­выми расходами пара через все ступени ЦНД и с отборами пара между ступенями. Далее для простоты изложения рассматриваются безотборные режимы.

Сказанное позволяет считать, что изменение характеристик ЦНД при изменении режима работы - следствие воздействия внешней среды в контрольных сечениях.

При испытаниях отсеков ЦНД давление и температура пара на входе в него могут быть измерены достаточно точно. Из парамет­ров влажного пара в выходном сечении надежно может быть измерено только статическое давление , что недостаточно для определе­ния состояния пара в этом сечении по данным прямых измерений. В ре­зультате не могут быть найдены экспериментальные характеристики ЦНД в функции интегрального изменения состояния пара в нем при реальном процессе истечения. Однако измерения , и позволяют характеризовать интегральное изменение состояния среды при адиаба­тическом и изоэнтропическом течении между контрольными сечениями, т.е. изменение ее состояния в идеальном ЦНД.

При фиксированных , и интегральные изменения среды в идеальном и реальном ЦНД будут различны, однако при одина­ковой частоте вращения ротора и их геометрических характеристиках должно выполняться условие однозначности: конкретному интегральному изменению состояния среды в идеальном ЦYД соответствует только одно изменение среды в реальном ЦНД. Или, проще, в виде постулата: изме­нение интегрального состояния среды в отсеке на произвольном режиме работы является функцией изменения этого состояния при изоэнтропическом процессе с теми же , , .

Принятый постулат позволяет представлять характеристики реаль­ного ЦНД в виде функции характеристик изменения состояния среды в идеальном ЦНД. Эти характеристики следует искать в виде комплек­сов, от которых зависит упомянутое изменение состояния, и формиро­вать из размерных параметров состояния, относящихся к контрольным сечениям.

Такие комплексы рационально выбирать на основе теории подобия, которая в числе прочих задач занимается представлением процессов изменения состояния сред, движущихся между начальными и конечными сечениями трактов. В зависимости от заданных граничных условий таким процессом может являться изменение состояния потока при пере­ходе от одного, сечения ЦНД к другому, или процесс перехода от состояния торможения к состоянию движущейся среды в пределах конкретного сечения.

На основании - теоремы теории подобия и размерностей связь между размерными переменными, описывающими этот процесс, может быть представлена в виде связи между числами подобия. Для того чтобы задать состояние среды в потоке, достаточно задать лобую пару независимых термических параметров состояния. Аналогично, для определе­ния процесса перехода от состояния торможения к состоянию потока в конкретном сечении в функции чисел подобия достаточно задать два из них. Остальные, число и вид которых зависят от физической приро­ды и особенностей процесса течения, оказываются функциями задан­ных. Сказанное относится и истечению между конкретными сечениями отсека ЦНД.

Напомним, что теория подобия не дает указаний, как выбирать размерные физические величины, входящие в числа подобия. Она не несет информации, позволяющей выбрать набор чисел подобия, являющихся достаточным в условиях произвольной задачи. В каждом конкретном случае этот выбор определяется постановкой задачи и граничными условиями, при которых она решается, т.е. принятой схемой, или моделью течения. В связи с этим в каждом конкретной случае речь может идти только о выборе необходимых чисел подобия. Достаточность их набора определяется достаточностью используемой моде­ли течения применительно к реальному.

Исходя из сказанного, перейдем к формулировке модели течения рабочей среды в ЦНД. Эта модель должна включать в себя:

- граничные условия в контрольных сечениях ЦНД, определяющие термогазодинамические параметры потока в них;

- геометрические и газодинамические характеристики лопаточных венцов;

- допущения о процессах изменения состояния пара, происходящих в них;

- аналитические зависимости, связывающие рабочие характерис­тики проточной части с числами подобия.

Проточная часть ЦНД формируется из нескольких турбинных ступе­ней. Условия течения в любой из них определяются местом ступени в отсеке и граничными условиями на входе и выходе из ЦНД. Из условий однозначности следует, что конкретному сочетанию этих граничных ус­ловий соответствует единственный режим работы и интегральное изменение состояния среды в ЦНД, а, следовательно, и единственно возможное изменение ее состояния в каждой из ступеней. С другой стороны, конкретному режиму работы любой ступени отсека соответст­вует единственное сочетание граничных условий в его контрольных сечениях. Наличие такой взаимосвязи позволяет упростить задачу и рассматривать интегральное изменение состояния рабочей среда в ЦВД, основываясь на модели изменения этого состояния в ступени ЦНД.

Опишем ее, конкретизируя общие требования, названные выше для модели течения в ЦНД. Будем полагать, что в качестве рабочего та­ла используется вязкая сжимаемая гомогенная среда, термические параметры которой связаны уравнением Менделеева-Клапейрона. Про­цесс изменения состояния рабочей среды в ступени на конкретном режиме является квазиустановившимся, по отношению к окружающей среде - адиабатическим.

Интегральные характеристики ступени, как и характеристики ЦНД, строятся на основе параметров рабочей среды, осредненных по контрольным сечениям ступени (0, 1, 2, о которых говорилось в гл.1). Геометрические размеры ступени в них известны. Протечки рабочей среды между ротором и неподвижными элементами конструкции ступени отсутствуют. В качестве характеристик рабочей ступени рассматриваем коэффициент расхода и коэффициент полезного действия, определения которых даны в предыдущих главах.

Коэффициент полезного действия определяется величинами коэф­фициентов потерь в сопловом венце ( ), в рабочем венце ( ) и зависит от потерь с выходной скоростью. На конкретном режиме эти коэффициенты, как и коэффициенты расхода , - постоянные величины. Если исследуется работа ступени на переменных режимах, то следует использовать экспериментальные зависимости этих коэффициентов от условий течения:

(5.11)

Как отмечено выше, количество и вид чисел подобия, функциями которых являются представляемые коэффициенты, зависят от использу­емой модели течения в лопаточном венце. Запись в выражениях (5.11) величин , , соответствующих изоэнтропическому процессу те­чения, при представлении экспериментальных данных вытекает из одно­значности, при прочих равных условиях, связи идеальных и реальных потоков.

Далее предполагаем, что зависимости вида (5.11) имеют место, и поэтому рассматриваем произвольный режим работы ступени. Набор чисел подобия, необходимых для представления характеристик ступени и зависимостей (5.11), найдется из уравнений, описывающих рассмат­риваемую одномерную модель течения, после представления их в безразмерном виде.

Запишем систему используемых уравнений.

Уравнение состояния:

. (5.12)

Уравнение энергии:

. (5.13)

Уравнение количества движения:

. (5.14)

(Напомним, что уравнения (5.12)-(5.14) записаны для 1 кг рабочей среды.)

Уравнение неразрывности по торцевым контрольным сечениям

или иначе:

. (5.15)

Уравнение расхода через сопловой венец:

. (5.16)

Уравнение расхода через рабочий венец:

. (5.17)

Уравнение идеальной адиабаты:

. (5.18)

Искомой характеристикой ступени является относительная величина необратимых потерь механической энергии в ступени , опре­деляемая из уравнений (5.12)-(5.18).

Дополним эту систему уравнений кинематическими соотношениями на основании треугольников скоростей:

, (5.19)

. (5.20)

Обратимся к уравнению энергии (5.13), переписав его так:

. (5.21)

Обозначим количество теплоты, которая эквивалентна работе, затраченной на преодоление сил сопротивления при расширении рабочей среды в ступени. Полагаем условно, что эта теплота подво­дится к рабочей среде при . Тогда:

. (5.22)

Перепишем уравнение (5.21) с учетом формулы (5.22) и уравне­ния Эйлера (5.14):

. (5.23)

Используем термодинамическую степень реактивности ступени

. (5.24)

В соответствии с рис.3.4:

, (5.25)

.

Используя соотношения (1.21), (1.22), (1.29), (1.30), а также равенства (5.19), (5.20), (5.24), (5.25), преобразуем уравнение (5.23):

(5.26)

Определим критическую скорость по параметрам торможения перед ступенью:

, (5.27)

где - скорость звука в данной среде по параметрам торможения.

Введем приведенные скорости:

, (5.28)

В соответствии с рис.3.2 и формулами (5.24), (5.25)

. (5.29)

Обозначим:

, .

C учетом принятых соотношений и обозначений уравнение (5.26) после преобразований принимает следующий вид:

, (5.30)

Здесь

. (5.31)

В уравнении (5.30) присутствуют в явном виде кроме определяемой величины три неизвестных, определяющих ее: , , . Для того, чтобы найти связь между ними, обратимся сперва к уравне­нию (5.15) и, преобразовав его, приведем к квадратному уравнению относительно . При решении этого уравнения заменим по формуле (5.29) и примем приближенно:

.

После этого получим окончательно:

. (5.32)

Здесь

,

.

В числителе формулы (5.32) сохранен знак «+» перед членом А, ибо знак «-» дает решение, не имеющее физического смысла.

Используем уравнения (5.16) и (5.17), приравняв их правые части:

. (5.33)

Вводя в рассмотрение и , принимая для простоты ; , связывая параметры торможения абсолютного и относительного движения, преобразуем выражение (5.33):

где

.

Входящие в формулу (5.34) приведенные скорости и определяются из выражений (5.19), (5.20) и (5.31)

, (5.35)

. (5.36)

В трех результирующих уравнениях (5.30), (5.32), (5.34) фигурируют гео-метрические параметры ступени, которые известны. Входящие в уравнения ко-эффициенты потерь и расхода на конкретном режиме - постоянные числа. Не-известными, подлежащими определению, являются четыре величины: , , , . Таким образом, полученная система уравнений не замкнута. Однако ее можно рассматривать, как записанную в параметрической форме. Задаваясь численным значением величины, выбранной в качестве параметра из неизвест-ных , , , мы при известном и постоянной частоте вращения уменьшаем число определяемых величин до двух, что делает систему уравне-ний замкнутой и позволяет найти оставшиеся неизвестные из уравнений (5.32), (5.34). Далее из уравнения (5.30) находится и .

Таким образом мы снова вернулись к полученному ранее результату: ин-тегральное изменение состояния рабочей среды в ступени задано, если заданы два числа подобия этого процесса. Важно отметить, что если заданы например, и , то при этом единственные значения принимают не только и , но также и любые числа подобия, отражающие другие особенности процесса течения и входящие в функциональные зависимости (5.11).

Если рассматривать переменные режимы работы ступени, то сказанное позволяет ожидать, что между числами подобия существуют однозначные за-висимости:

= ( ), = ( ) (5.37)

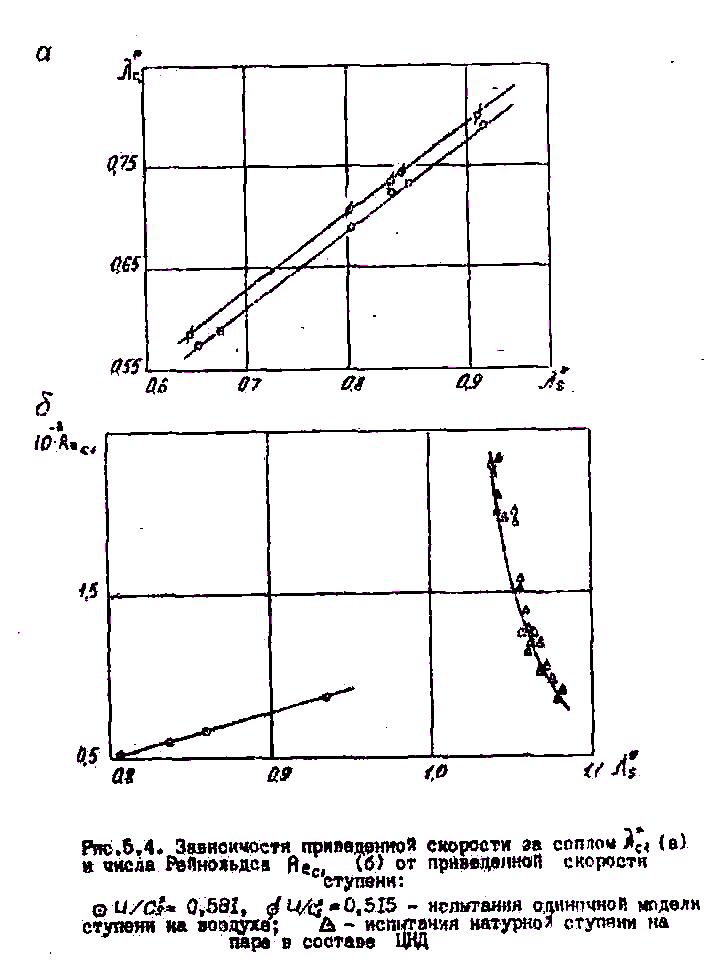
С другой стороны, из-за влияния на них граничных условий течения, эти зависимости могут существенно отличаться для одной и той же ступени при работе ее как одиночной, так и в составе отсека ступеней. Экспериментальные зависимости (5.37), подтверждающие это, приведены для ступени ЦНД на рис.5.4 по данным испытаний ее модели в экспериментальной воздушной тур-бине и по материалам испытаний в составе натурного ЦНД, проведенных ЛМЗ.

Наличие зависимостей вида (5.37) и других, подобных им, позволяет представлять характеристики ступени в отсеке ЦНД в функции любого из чисел подобия, найденных для ступени. Это относится и к величине , определяемой формулой (5.30). Пусть = f ( ) .

Если обозначить кпд ступени (без использования выходной скорости) и относительную потерю энергии с выходной скоростью , то:

. (5.38)

Легко показать, что

,

где .

В соответствии со сказанным выше , .

Из формулы (5.38) следует, что .

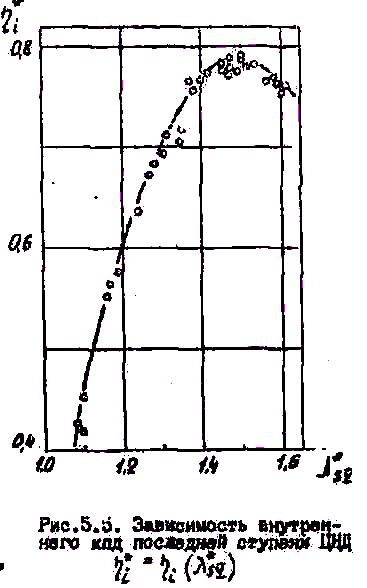
Для последней ступени натурного ЦНД на рис.5.5 представлена экспери-ментальная зависимость . Использование в ней внутреннего кпд связано с невозможностью определить лопаточный кпд ступени отсека по дан-ным интегральных испытаний. На рис.5.6 показана зависимость коэффициента расхода соплового венца той же ступени от , определенного в со-ответствии с формулой (5.16): .

Вместе с исходными данными и допущениями, принятыми при записи уравнений (5.30), (5.32), (5.34), их можно рассматривать как уравнения физической модели интегрального изменения состояния рабочей среды в ступени ЦНД на конкретном режиме, представленные в виде функции чисел подобия. Численные значения , , , получаемые при решении уравнений (5.32), (5.34) зависят, кроме геометрических параметров ступени от величин коэффициентов , , , . Согласно формулам (5.11) последние, в свою очередь, оказываются функциями условий течения, определяемых упомянутыми уравнениями. Поэтому при рассмотрении переменных режимов к системе уравнений (5.32), (5.34) следует добавить совокупность (5.11).

Представленные уравнения были записаны для одиночной ступени, по-этому при их решении параметры потока на входе и выходе известны из гра-ничных условий. Для ступеней в составе отсека эти уравнения следовало бы дополнить уравнениями (5.15)-(5.17), записанными для соседних венцов соседних ступеней отсека с учетом граничных условий между ними. Граничные условия на входе в отсек явились бы условиями перед сопловым венцом первой ступени, граничные условия на выходе из отсека - условиями за рабочим венцом последней ступени. В комплексе записанные таким образом уравнения для всех венцов отсека вместе с его граничными условиями составили бы физическую модель изменения интегрального состояния среды в ЦНД.

В настоящее время формулировка такой модели неосуществима хотя бы из-за отсутствия необходимой информации в виде зависимостей (5.11) для всех венцов рабочих и сопловых лопаток ЦНД. Однако принципиальная возмож-ность ее формулировки позволяет, не записывая необходимых уравнений и не решая их, представить экспериментальные характеристики ступеней ЦНД в функции чисел подобия, показанных выше. Кроме того, становится обоснован-ным и представление экспериментальных зависимостей, связывающих числа подобия разных ступеней. Так, на рис.5.7 представлена экспериментальная за-висимость последней ступени ЦНД, на рис.5.8 зависимость для второй и последней ступеней отсека.

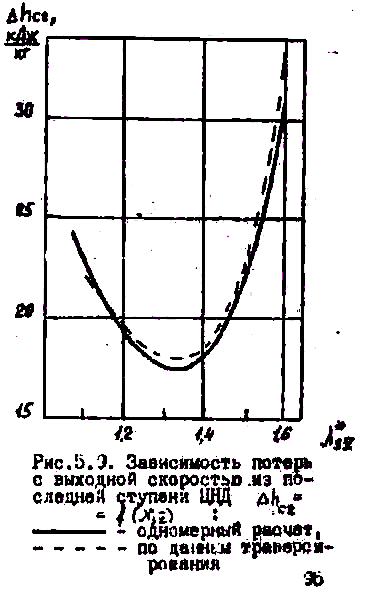
Следует заметить, что результаты выполненных газодинамических расчетов ступеней отсека по одномерной теории в части, не зависящей от использованных эмпирических коэффициентов, согласуются с экспериментальными характеристиками, определенными на основе этой теории. На рис.5.9 показана экспериментальная и расчетная зависимости потери с выходной скоростью для последней ступени ЦНД. Экспериментальная зависмимость получена при обработке данных траверсирования потока по радиусу за ступенью и осреднении их для этого сечения, расчетная – по данным одномерного теплового расчета. Сходимость расчета и опыта достаточно хорошая.

В заключение заметим, что зависимость характеристик ступеней от гра-ничных условий, о которых говорилось при рассмотрении рис.5.4, проявляется и при работе ступени в группе. Как показали опыты ЛМЗ на паре расход-ная характеристика второй ступени натурного ЦНД с последней лопат-кой =1200 мм отличается от упомянутой характеристики второй ступени при замене только последеней ступени ЦНД на ступень с рабочей лопаткой =1000 мм (рис.5.10).

СПИСОК ЛИТЕРАТУРЫ

1. Елизаров В.С. Введение в теорию турбинной ступени. – Л.: Изд-во Пимаш (ЛМЗ-ВТУЗ), 1983. – 46 с.

2. Елизаров В.С. Использование осесимметричной теории турбинной ступени в газодинамических расчетах лопаточного аппарата. – Л.: Изд-во Пимаш (ЛМЗ- ВТУЗ), 1989. – 86 с.

3. Дейч М.Е., Зарянкин А.Е. Гидродинамика. – М.: Энергоатомиздат, 1984. – 384 с.

4. Щегляев А.В. Паровые турбины. – М.: Энергия, 1976. –357 с.

5. Самойлович Г.С., Троянский Б.М. Переменные и переходные режимы в паровых турбинах. – М.: Энергоатомиздат, 1982. – 495 с.