4.2. Рабочий процесс в колесах скорости

Ограничиваясь при тепловом расчете двухвенечным колесом ско­рости рабочий процесс в ступени можно рассматривать последовательно для первой и второй пары венцов. Обозначения контрольных сечений можно при этом принять в соответствии с рис.4.1.

Изображение в диаграмме I - S процесса, происходящего в пер­вой паре венцов (в ступени давления), не отличается от того, как это делалось для обычной ступени давления. Что же касается направ­ляющего и второго рабочего венцов, т.е. ступени скорости, то для нее рабочий процесс отличается лишь весьма большими значениями кинетической энергии потока, входящего в ступень: . Кроме того, изоэнтропические перепады и , срабатываемые в направляющем и втором рабочем венцах, либо малы, либо отсутствуют. Поэтому, если не учитывать влияния протечек, мож­но считать, что работа на втором и последующих (если они имеются) рабочих венцах происходит в основном не за счет расширения рабочего тела, а за счет использования кинетической энергии , соответствующей выходной скорости из первого рабочего венца.

Несмотря на аналогичность изображения рабочего процесса колеса скорости и одновенечной ступени давления в диаграмме I - S тепло­вой расчет колеса скорости недостаточно надежен и обычно его кпд берется на основании экспериментальных данных. Это связано с осо­бенностями конструкции двухвенечного колеса (малые высоты облопачивания, часто - парциальный впуск рабочего тела) и рабочего про­цесса в нем (большие скорости течения, влияние сжимаемости и воз­никновение скачков уплотнения).

Отмеченные особенности приводят к существенному снижению ско­ростных коэффициентов и направляющих и рабочих венцов из-за больших концевых и волновых потерь. Экспериментальных данных, позволяющих обоснованно учесть это снижение, на сегодняшний день недостаточно. Признано более рациональным использовать для тепловых расчетов экспериментальные данные об изменении кпд двухвенечных ко­лес (или их моделей) на переменных режимах, нежели определять этот кпд в процессе расчета, учитывая составляющие потерь. Однако такой расчет представляет интерес с точки зрения оценки величины .

Найдем относительный кпд на лопатках двухвенечной ступени. Условимся указывать количеством надстрочных индексов - штрихов, к какой паре венцов относится та или иная величина. Так, например: , - степени реактивности первого и второго рабочих венцов соответст­венно.

Для выявления основных зависимостей, определяющих кпд на ло­патках двухвенечной ступени, выведем соответствующее выражение этого кпд, подобно тому, как выводилась формула Банки.

Сделаем это при следующих допущениях:

- ступень чисто активная: , , следова­тельно, ни на рабочих венцах, ни на направляющем венце ступени скорости нет расширения потока, связанного с наличием перепада давлений на венец;

- лопатки для рабочих венцов и направляющего венца второй ступени скорости выбраны из условия симметричности; для первого рабочего венца ; для направляющего венца - ; для второго рабочего венца (профиль сопла не симмет­ричен);

- скоростные коэффициенты всех венцов, кроме соплового (а значит, и соответствующие коэффициенты потерь), одинаковы: ;

• ступень является чисто осевой, постановка задачи - одномерная.

В соответствии с турбинным уравнением Эйлера выражение для от­носительного кпд на лопатках двухвенечной ступени можно записать в следующем виде:

. (4.1)

Находим окружные составляющие скоростей, стоящие в числителе отношения (4.1), путем последовательных подстановок, как это дела­лось при выводе формулы Банки, и с учетом треугольников скоростей, построенных для двухвенечной ступени (рис.4.3):

,

Подставляя в выражение (4.1) вместо величин, заключенных в квадратные скобки, их значения, запишем формулу для кпд двухвеначного колеса:

. (4.2)

Из выражения (4.2) видно, что =0 при =0 и при .

Очевидно, что если не принимать во внимание зависимость коэф­фициентов и от отношения , функция = ( ) для двухвенечного колеса со ступенями скорости, также как для одновенечного, представляет собой параболу.

Как и прежде, найдем величину , соответствующую мак­симуму кпд , взяв производную от правой части выражения (4.2) по переменной и приравняв эту производную нулю. Оказыва­ется, что

, (4.3)

где .

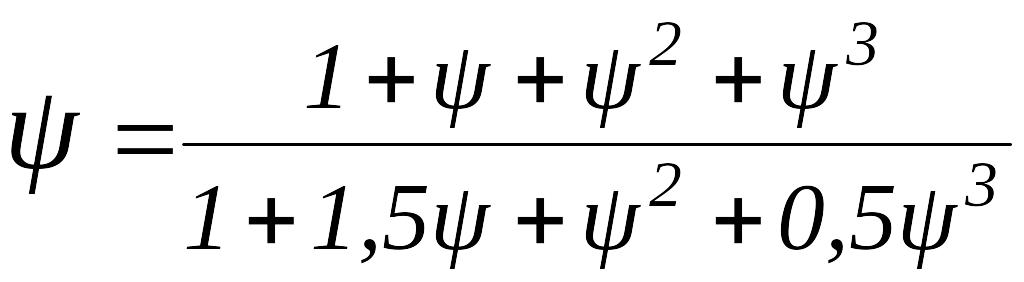При изменении коэффициента в диапазоне 0,8 < < 1 отно­шение меняется слабо: 0,96 < < 1. Поэтому, значение практически не сказывается на величине .

Таким образом:

- для одновенечной ступени давления:

;

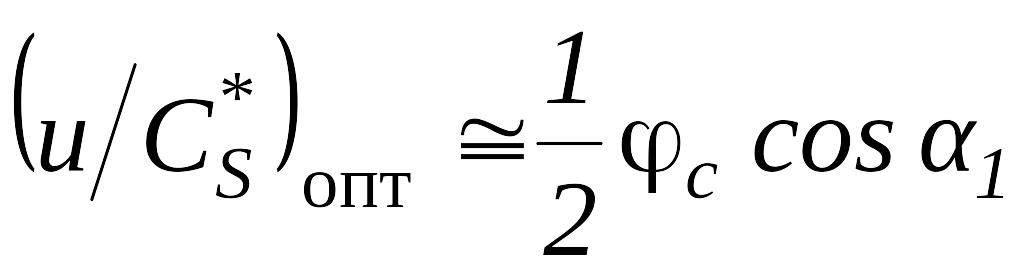- для ступени с двухвенечным колесом скорости:

; (4.4)

- для ступени с трехвенечным колесом скорости:

.

Как уже говорилось, во всех этих случаях зависимость кпд от отношения носит параболический характер, что в первую очередь определяется потерями с выходной скоростью. Из приведенных выше соотношений видно, что оптимальное значение отношения уменьшается обратно пропорционально числу подвижных венцов.

Таблица 4.1