
- •Раздел 2
- •1.1. Основные уравнения одномерного движения
- •Уравнение состояния
- •Уравнение неразрывности
- •Уравнение количества движения
- •1.2. Газодинамические характеристики лопаточных венцов
- •1.3. Треугольники скоростей
- •Из рассмотренных треугольников скоростей вытекают следующие очевидные соотношения:
- •2. Тепловой расчет осевой турбинной ступени
- •2.1. Рабочий процесс в соплах, его построение в I - s – диаграмме и определение скоростей
- •2.2. Процесс в рабочих лопатках, его построение
- •2.3. Определение проходных площадей и высот облопачивания
- •3. Лопаточный коэффициент полезного действия
- •3.1. Вводные замечания и определения
- •3.2. Лопаточный кпд чисто осевой активной
- •Анализ формулы Банки
- •3.3. Лопаточный кпд турбинной ступени в общем случае
- •4. Ступени с колесами скорости
- •4.1. Назначение и устройство колес скорости
- •4.2. Рабочий процесс в колесах скорости
- •Основные характеристики ступеней
- •4.3. Некоторые практические данные по колесам скорости
- •Типовая комбинация кс-1а
- •5.1. Нерасчетные режимы работы одиночных ступеней
- •Ступени с малыми дозвуковыми скоростями
- •5.2. Нерасчетные режимы ступеней паровой турбины при работе их в составе отсека
- •Оглавление
Анализ формулы Банки
Зависимость от отношения и других факторов
Формула Банки определяет лопаточный кпд чисто активной ступени как функцию:
- отношения , однозначно связанного с числом Струхаля Sh [3];
- углов , , определяемых геометрическими соотношениями профилей и лопаточных венцов;
-
скоростных коэффициентов
и
,
в свою очередь зависящих от этих
соотношений и параметров
и
![]() [3].
[3].
Таким образом, как и следовало ожидать, рассматриваемый кпд зависит от основных критериев работы ступени: отношения (Sh) и, в неявном виде, от и .
Считая, что ступень работает в зоне автомодельности по и рассмотрим влияние тех переменных, которые непосредственно, в явном виде, входят в выражение (3.17). В этом случае определяющим является влияние на кпд отношения .
Оценивая роль этого критерия, полагаем угол =const (сопловой аппарат при разных неизменен) и, следовательно, в условиях автомодельности =cost .
Изменение
отношения
![]() и коэффициента
при изменении
является слабым и, как показали расчеты
на ЭВМ, при изучении зависимости кпд от
можно полагать
и
постоянными. Напомним еще раз, что
каждому, отношению
соответствуют свои рабочие лопатки.
и коэффициента
при изменении
является слабым и, как показали расчеты
на ЭВМ, при изучении зависимости кпд от
можно полагать
и
постоянными. Напомним еще раз, что
каждому, отношению
соответствуют свои рабочие лопатки.
При
этих условиях лопаточный кпд
является квадратичной функцией отношения
.
Легко видеть, что
=
0 при
=0
и при
![]() ,
так что функция
=
(
)
должна иметь максимум в промежутке
указанных значений
.
,
так что функция
=
(
)
должна иметь максимум в промежутке
указанных значений
.
Величину ( )ОПТ (соответствующую максимальному значению кпд ( )МАХ ) можно найти, взяв производную от выражения (3.17) по (при сделанных выше допущениях) и приравняв ее нулю:
 .
.
Далее получим:
![]() (3.18)
(3.18)
Для одиночной активной ступени, выходная скорость которой не используется, при обычно применяемых значениях и
![]() .
.
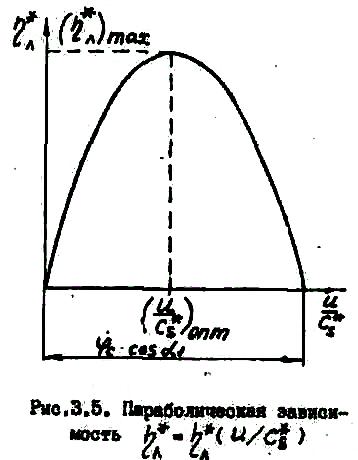
Зависимость = ( ) представлена на рис.3.5 в виде параболы. Максимальное значение кпд ( )мах находим после подстановки правой части уравнения (3.18) в уравнение (3.17) вместо отношения , оно будет следующим:
![]() .
(3.19)
.
(3.19)
Выясним причины параболического характера зависимости = ( ), представленной на рис.3.5. Для этого, прежде всего, построим треугольники скоростей, характерные для трех случаев:
![]() ,
,
![]() ,
,
![]()
Это построение выполнено при =const. Для большей наглядности принято:
-
отношение
изменяется
за счет окружной скорости u
при
неизменной скорости
![]() =
idem
(при этом (
=
idem
(при этом (![]() )=idem
и располагаемый изоэнтропический
перепад энтальпий на ступень не
меняется;
)=idem
и располагаемый изоэнтропический
перепад энтальпий на ступень не
меняется;
-
=
0 при всех отношениях
.
Следовательно,
![]() и сжимаемость не влияет на течение;
и сжимаемость не влияет на течение;
-
![]() при любом отношении
,
хотя и не постоянны при его изменении;
при любом отношении
,
хотя и не постоянны при его изменении;
- и не зависят от .
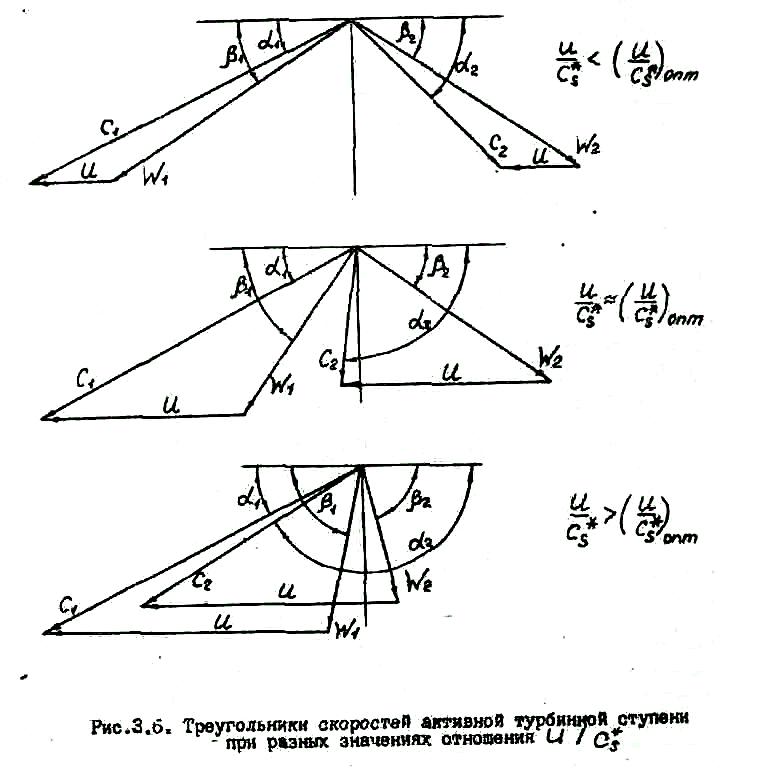
Треугольники скоростей, построенные, исходя из этих допущений, показаны на рис.3.6. С их помощью рассмотрим одновременное изменение с отдельных составляющих потерь энергии, пользуясь энергетической формой представления кпд ступени. В соответствии с формулами (3.6)
![]() .
.
Величину
![]() можно
раскрыть так:
можно
раскрыть так:

(учитывая,
что при
=
0,
![]() ).
).
Величина
оказывается не зависящей от отношения
.
Аналогично раскрывается величина
![]() :
:
 .
.
Как было показано выше,
![]() .
.
При
=
0,
![]() и
и
![]() .
Из рис.3.6 видно, что
.
Из рис.3.6 видно, что
![]() становится меньше при увеличении
отношения
вплоть до
=
становится меньше при увеличении
отношения
вплоть до
=![]() .
Соответственно, монотонно уменьшается
и
.
Соответственно, монотонно уменьшается
и
![]() ,
так что и эта составляющая потерь не
может вызвать параболический характер
зависимости. [Заметим, что в пределе
при
,
так что и эта составляющая потерь не
может вызвать параболический характер
зависимости. [Заметим, что в пределе
при
![]() =
,
поскольку
при этом
=
,
поскольку
при этом
![]() и
и
![]() .]
.]
Относительная потеря энергии с выходной скоростью
 .
.
![]() может
быть представлена функцией от
,
однако она оказывается неявной.
может
быть представлена функцией от
,
однако она оказывается неявной.
Из
рассмотрения треугольников скоростей,
представленных на рис.3.6, следует, что
выходная скорость
при неизменной
с ростом
сперва убывает, затем возрастает. Также
меняется отношение
![]() .
Таким образом, параболический характер
зависимости
=
(
)
в основном определяется изменением
относительной потери энергии с выходной
скоростью, так как при прочих равных
условиях
возрастает
при отклонении отношения
от оптимального значения. Этот результат,
а также соотношение величин относительных
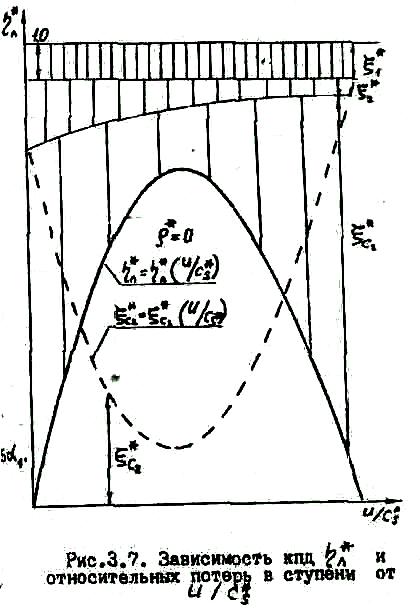
потерь в ступени показаны на рис.3.7. Если
значения
близки
к оптимальным, то потери с выходной
скоростью имеют тот же порядок величины,
что и сумма потерь в лопаточных
венцах. При неоптимальных
потери с выходной скоростью существенно
превышают потери в соплах и рабочих
лопатках.
.
Таким образом, параболический характер
зависимости
=
(
)
в основном определяется изменением
относительной потери энергии с выходной
скоростью, так как при прочих равных
условиях
возрастает
при отклонении отношения
от оптимального значения. Этот результат,
а также соотношение величин относительных
потерь в ступени показаны на рис.3.7. Если
значения
близки
к оптимальным, то потери с выходной
скоростью имеют тот же порядок величины,
что и сумма потерь в лопаточных
венцах. При неоптимальных
потери с выходной скоростью существенно
превышают потери в соплах и рабочих
лопатках.
Интересно отметить, что при =( )опт выход потока из ступени - неосевой. Легко показать, что в этом случае:
![]()
 .
.
Поскольку
![]() <2,
выражение, заключенное в квадратные
скобки в последней формуле, положительно,
вследствие чего
>0.
Это говорит о том, что при
=(
)опт
угол
>90°.
<2,
выражение, заключенное в квадратные
скобки в последней формуле, положительно,
вследствие чего
>0.
Это говорит о том, что при
=(
)опт
угол
>90°.
Важно отметить, что значение , соответствующее осевому выходу потока из ступени, а значит и минимуму относительных потерь энергии с выходной скоростыо , меньше, чем значение ( )опт.
Действительно, проведя соответствующие выкладки, получим:
![]() .
.
Величина
![]() < 1,
следовательно:
< 1,
следовательно:
![]() .
.
Сопоставляя величину ( ) с выражением (3.18), приходим к выводу:
( )<( )опт.
Заметим, что это соотношение сохраняется и при учете зависимости от , или при 0 .
Рассмотрим
теперь зависимость кпд ступени от угла
выхода потока из сопел
.
Этот угол явно влияет [см.
формулу
(3.17)] через
![]() и неявно - через скоростные коэффициенты
и
.
Если бы профильные и концевые потери,
связанные с эффектом вязкости, не
зависели от углов
,
и
,
то было бы рационально предельно снижать
для повышения величины
.
и неявно - через скоростные коэффициенты
и
.
Если бы профильные и концевые потери,
связанные с эффектом вязкости, не
зависели от углов
,
и
,
то было бы рационально предельно снижать
для повышения величины
.
В
действительности, как показано в [4] ,
при неизменной высоте облопачивания
уменьшение угла
приводит к увеличению профильных потерь
в соплах, а также к росту угла поворота
потока в сопловых и рабочих лопатках,
и в итоге - к снижению коэффициентов
и
.
Поэтому существуют оптимальные значения
=![]() .
Расчеты и опыты показывают, что для
активных ступеней со сравнительно
короткими лопатками
=
10-12
.
.
Расчеты и опыты показывают, что для
активных ступеней со сравнительно
короткими лопатками
=
10-12
.
Расчет по формуле (3.19) показывает, что для чисто активной ступени снижение на 1% вызывает снижение кпд на ~ 2%, тогда как снижение на 1% снижает кпд ступени лишь на ~ 0,5%, т.е. на величину, в четыре раза меньшую. Однако следует учитывать, что при значительных степенях реактивности ( > 0) это не так.
Напомним, что объектом приведенного анализа явилась теоретическая модель ступени, у которой изменение проходных площадей рабочих венцов от режима к режиму обеспечивало нулевую степень реактивности. Независимо от величины отношения , форма лопаток могла быть оптимальной при любом его значении, а угол - безударным. Такие особенности теоретической модели позволяют, с одной стороны, раздельно оценить влияние каждого из рассмотренных факторов и, с другой стороны, при любом значении оперировать минимальными величинами потерь в сопловых и рабочих лопатках и, следовательно, предельными для данного режима значениями лопаточного кпд. И то и другое весьма важно для понимания работы реальной ступени с неизменной геометрией проточной части. Поэтому дальнейший анализ также будем вести применительно к ее теоретической модели.
Основываясь на зависимостях, полученных для коэффициента ступени, кинетическая энергия потока на выходе, из которой не используется, перейдем к рассмотрению коэффициента ступени, выходная скорость которой используется.
Зависимость от и других факторов
Коэффициенты полезного действия и связаны выражением (3.10). Графики = ( ) и = ( ) ступени с конкретными значениями

угла и коэффициентов и , построенные на основе формулы Банки (3.15) и формулы (3.10) совмещены на рис.3.8. Из их рассмотрения следует, что:
- при одних и тех же значениях > ;
-
разность
![]() имеет
место за
счет
использования в следующей
ступени
кинетической энергии, соответствующей
выходной скорости из предыдущей
ступени;
имеет
место за
счет
использования в следующей
ступени
кинетической энергии, соответствующей
выходной скорости из предыдущей
ступени;
-
вблизи (
)ОПТ
разность
![]() невелика, при отклонении режима от
расчетного она возрастает;
невелика, при отклонении режима от
расчетного она возрастает;
- оптимум графика сдвинут в сторону больших значений по сравнению с оптимумом графика ;
- в области весьма малых и весьма больших график идет значительно круче графика .
В остальной области изменения зависимость = ( ) более полога, чем = ( ).
Таким образом, выигрыш в кпд вблизи ( )опт невелик, но увеличивается при отклонении от оптимального значения, так как этот выигрыш происходит за счет использования кинетической энергии, соответствующей выходной скорости, которая увеличивается по мере отклонения ( ) от оптимума.
Используя формулу (3.8), можно построить график зависимости кпд от ( ), представленный на рис.3.9. На этом же рисунке показаны графики
изменения
относительных потерь в соплах (![]() )
и в рабочих лопатках (
)
и в рабочих лопатках (![]() ).
Переменность относительных потерь в
соплах, наблюдаемая на рис.3.9, является
следствием переменности располагаемого
перепада
).
Переменность относительных потерь в
соплах, наблюдаемая на рис.3.9, является
следствием переменности располагаемого
перепада
![]() .
При
=
idem
перепад
зависит от отношения
,
поскольку изменение последнего
влияет на потери с выходной скоростью.
.
При
=
idem
перепад
зависит от отношения
,
поскольку изменение последнего
влияет на потери с выходной скоростью.
Разница
![]() ,
соответствующая режимам с (
,
соответствующая режимам с (![]() )ОПТ
и с (
)c2
u
обычно
невелика и часто за расчетное принимают
то отношение
,
при котором
)ОПТ
и с (
)c2
u
обычно
невелика и часто за расчетное принимают
то отношение
,
при котором
![]() .
.

Влияние угла на работу рассматриваемой ступени имеет тот же характер, что и для ступени без использования выходной скорости, но изменение кпд в зависимости от угла оказывается более слабым.
В конструкциях паровых и газовых турбин ступени с нулевой степенью реактивности ( =0) почти не применяются. Как правило, средняя степень реактивности в ступени положительна ( >0). Рассмотрим этот общий случай.
