73

Раздел 2

ИСПОЛЬЗОВАНИЕ ОДНОМЕРНОЙ ТЕОРИИ ТУРБИННОЙ СТУПЕНИ В ГАЗОДИНАМИЧЕСКИХ РАСЧЕТАХ ЛОПАТОЧНОГО АППАРАТА

1. осноВНЫЕ ПолоЖЕНИЯ одномерной теории

турбинной ступени

При проектировании ступеней турбин и их тепловом расчете за­дачей инженера является организация такого течения в лопаточных венцах, при котором необратимые потери механической энергии были бы минимальны. Как показано в работе [1], поток в лопаточном аппарате явля­ется пространственным. Газодинамический расчет ступени с учетом этого фактора оказывается достаточно сложным даже в предположении, что течение осесимметричное [2]. Расчеты и анализ работы ступеней существенно упрощается при введении допущений об установившемся движении и одномерности потока. Основываясь на них и учитывая струк­туру потока в ступени, показанную в [1], будем считать, что течение является установившимся для соплового венца в неподвижной системе координат, для рабочего - в связанной с ним подвижной системе коор­динат.

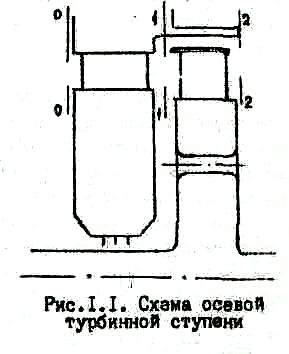
В соответствии со схемой осевой ступени (рис.1.1) обозначим индексами 0-0, 1-1, 2-2 контрольные сечения перед сопловым венцом, в межвенцовом зазоре и за рабочими лопатками ступени соответственно.

Учитывая, что наличие пара­зитных протечек в ступени вызывает появление неоднородности потока в контрольных сечениях, далее рассмат­риваем полностью уплотненную сту­пень, полагая для простоты, что она является чисто осевой.

Сочетание простых и ясных по­ложений одномерной теории с данными экспериментальных исследований яви­лись основой совершенствования проточных частей турбин вплоть до середины этого века. И в настоящее время одномерная теория турбомашин сохраняет самостоятельное зна­чение наряду с развитием изучения пространственного течения в турбомашинах и совершенствованием более точных методов двумерной тео­рии решеток и течения в ступени. В частности, на одномерной теории основано получение интегральных характеристик натурных и модельных ступеней при исследованиях их в экспериментальных турбинах.

1.1. Основные уравнения одномерного движения

сжимаемого газа

Общие законы сохранения, описывающие течение вязкого сжима­емого газа, излагаются в теоретическом курсе «Механика жидкости и газа». Ниже они рас­сматриваются в той мере, в какой это необходимо для осуществления газодинамических расчетов турбинных ступеней в рамках одномерной теории при сделанных выше допущениях.

Для расчетов течения сжимаемого газа, каковым является и во­дяной пар, далее используются следующие уравнения:

1) уравнение состояния;

2) уравнение неразрывности;

3) уравнение количества движения;

4) уравнение сохранения энергии.

Уравнение состояния

При анализе одномерных газовых процессов, а также в учебных целях, в качестве уравнения состояния используют уравнение Менделеева-Клапейрона

. (1.1)

Для перегретого и влажного водяного пара это уравнение не обеспечивает достаточную точность расчетов рабочего процесса паровых турбин. В практике применяют более сложные и более точные урав­нения состояния воды и водяного пара. Они представлены либо в виде различных графических интерпретаций (например, широко известная I-S - диаграмма), либо в виде аналитических аппроксимаций и программ для использования на ЭВМ, которые позволяют уменьшить погрешности, присущие графоаналитическому расчету при сохранении его наглядности.