2. Прямокутний паралелепіпед. Центральна симетрія паралелепіпеда.

Прямий паралелепіпед, у якого основою є прямокутник, називаєть­ся прямокутним паралелепіпедом

Усі грані прямокутного паралелепіпеда — прямокутники.

Усі діаго­налі прямокутного паралелепіпеда рівні.

Довжини непаралельних ребер прямокутного паралелепіпеда називають його розмірами (вимірами). У прямокутного паралелепіпеда три лінійні виміри.

Прямокутний паралелепіпед, у якого лінійні виміри рівні, нази­вається кубом.

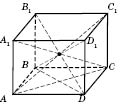Теорема. Діагоналі паралелепіпеда перетинаються в одній точці й точкою перетину діляться навпіл.

Із цього випливає, що точка перетину діагоналей паралелепіпеда є його центром си­метрії. У прямого паралелепіпеда є чотири діагоналі, які попарно дорівнюють одна одній. Теорема . У прямокутному паралелепіпеді всі діагоналі рівні. Квадрат діагоналі дорівнює сумі квадратів трьох його вимірів.

Білет № 13

1. Функція у = tg x, її графік і властивості.

2. Аксіоми стереометрії. Існування площини, що проходить через дану пряму і дану точку.

3. Обчисліть площу фігури, обмеженої лініями у = х² – 6х + 9, у = 5 – х.

4. Прямокутний трикутник з катетом а і протилежним кутом обертається навколо прямої, що містить його гіпотенузу. Знайдіть об’єм тіла обертання.

1. Функція у = tg x, її графік і властивості.

Тригонометричними називають функції, задані формулами:

y = sinх, y = cos x, y = tg x, y = ctg x.

Крива, яка є графіком функції y = cos x, називається тангенсої­дою.

Властивості функції y = tgх: 1. Обл. визначення – всі дійсні числа, крім точок (π/2+2πn), n є Z. 2. Область значень – проміжок (-∞;+∞). 3. Функція непарна, періодична з періодом Т = π. 4. Нулі функції – точки ( πn;0), n є Z. 5. Функція зростає на всій області визначення. 6. Функція не має екстремумів.

2. Аксіоми стереометрії. Існування площини, що проходить через дану пряму і дану точку.

I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою. IV. Пряма, що належить площині, розбиває цю площину на дві півплощини. V. Кожний кут має певну градусну міру, більшу від нуля. Розгорнутий кут дорівнює . Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами. VI. На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної дов­жи­ни, й тільки один. VII. Від півпрямої на площині, що містить її, можна відкласти в задану півплощину кут із даною градусною мірою, меншою за , і тільки один. VIII. Який би не був трикутник, існує трикутник, що дорівнює йому, у даній площині в заданому розміщені відносно даної півпрямої у цій площині. IX. На площині через дану точку, що не лежить на даній прямій, можна провести не більш як одну пряму, паралельну даній. До цих аксіом додаються три аксіоми ­групи С.

. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй. . Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку. . Якщо дві різні прямі мають спільну точку, то через них можна провести площину, й до того ж тільки одну.

Теорема . Через пряму і точку, яка не лежить на ній, можна провести площину, й до того ж тільки одну.

Нехай АВ – дана пряма і С – точка, яка їй не належить (рис. 11).

Доведення (існування площини)

Твердження	Аргумент
Візьмемо точку D, яка лежить на прямій АВ	І
Через точки D і С проведемо пряму DC	І
Через прямі АВ і DC проведемо площину α	С3

Доведення (єдиність площини) Доведемо від супротивного. Припустимо, що існує дві площини α і β, які проходять через пряму АВ і, точку С. За аксіомою С₂ площини α і β перетинаються по прямій, якій належать А, В, С, що суперечить умові. Отже, площина, яка проходить через пряму і точку, що не належить прямій, єдина.

Білет № 14

1. Залежність між тригонометричними функціями одного і того самого аргументу.

2. Циліндр. Формули об’єму циліндра та площі повної поверхні циліндра.

3. Розв’яжіть рівняння: (х² – 4х + 3) 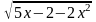= 0.

4. З точки А до площини проведено похилі АВ і АС, які утворюють з площиною кути по 60⁰. Знайдіть відстань між точками В і С, якщо ВАС = 90⁰, а відстань від точки А до площини дорівнює 3 см.