2. Поняття про статистику. Мода, медіана, середні значення.

Статистика – наука, що збирає, обробляє і вивчає різні дані, пов’язані з різними масовими явищами, процесами, подіями. Предметом вивчення статистики є вивчення кількісної сторони цих явищ.

Математична статистика – розділ математики, присвячений математичним методам систематизації, обробки та дослідження статистичних даних для наукових і практичних висновків.

Статистичне спостереження – це спланований, науково організований збір масових даних про соціально-економічні явища та процеси.

Основні поняття математичної статистики

1. Статистичні дані — сукупність чисел, які дають кількісну характеристику ознак певних об'єктів та явищ, що нас цікавлять.

2. Відібрану для спостереження сукупність об'єктів називають вибірковою сукупністю або вибіркою.

3. Кількість об'єктів сукупності називають об'ємом сукупності.

4. Числа, що є значеннями ознак кожної групи, на які можна поділити вибірку, називають варіантами; послідовність варіант називають варіаційним рядом.

5. Частоти — числа, які показують, скільки разів повторювалось кожне значення ознаки сукупності.

6. Відношення частоти до об'єму вибірки називають відносною частотою.

Вибірка характеризується центральними тенденціями: середнім значенням, модою і медіаною. Середнім значенням вибірки називається середнє арифметичне всіх її значень: 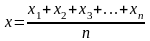де x_i — значення ознаки (варіанти); п — число одиниць сукупності

Мода вибірки – те її значення, яке трапляється найчастіше. Позначається Мо.

Медіана вибірки – це число, яке “поділяє” “навпіл” упорядковану сукупність усіх значень вибірки, тобто середня величина змінюваної ознаки, яка міститься в середині ряду, розміщеного в порядку зростання або спадання ознаки. Позначається Ме.

Білет № 9

1. Числові послідовності та їх класифікація.

2. Перпендикулярність площин. Ознака перпендикулярності площин.

3. Знайдіть область визначення функції y = lg(3x – 2x² – x³).

4. Висота конуса дорівнює Н. кут між висотою та твірною дорівнює 30⁰. Обчислити площу перерізу, проведеного через дві твірні, кут між якими дорівнює 60⁰.

1. Числові послідовності та їх класифікація

Числовою послідовністю називається функція, яка задана на множині всіх натуральних чисел або на множині перших п натуральних чисел.

Числова послідовність позначається так: (а_п): а₁; а₂; а₃; ...; а_п.

Кожне число а_п — п-й член послідовності; п — номер члена.

Види числових послідовностей:

1. Якщо кількість членів п послідовності (а_п) скінченна, то (а_п) — скінченна послідовність.

Якщо кількість членів п послідовності (а_п) нескінченна, то (а_п) — нескінченна послідовність.

Приклади:

а) послідовність (а_п) натуральних чисел нескінченна;

б) послідовність (а_п) коренів рівняння (х – 1)(х – 2)(х + 3) = 0 скінченна.

2. Якщо кожний наступний член послідовності, починаючи з другого, більший за попередній, то послідовність є зрос­таючою.

Якщо кожний член послідовності, починаючи з другого, менший від попереднього, то послідовність є спадною.

Приклади:

а) (а_п): 1; 2; 3; ... — послідовність натуральних чисел є зростаючою;

б) (b_п): -1; -2; -3; ... — послідовність цілих від'ємних чисел є спадною.